Post type: WirisQuizzes

Categories
Uncategorized

How to Calculate the Area Between Two Curves?

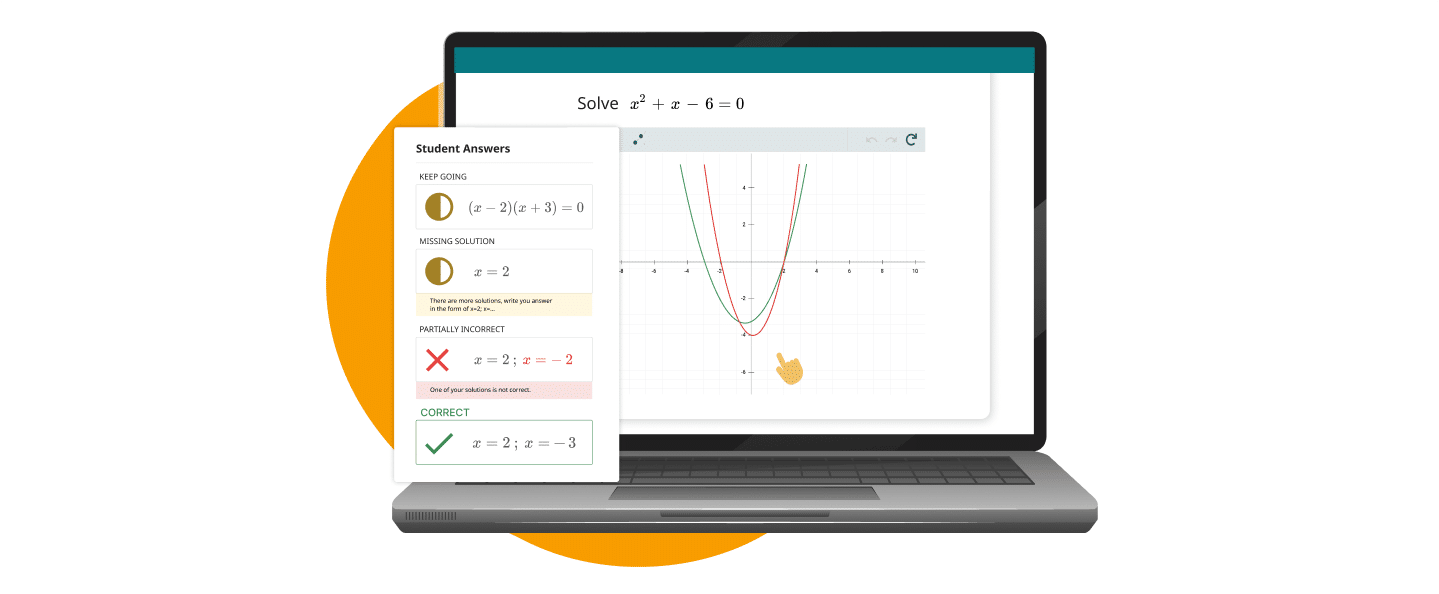
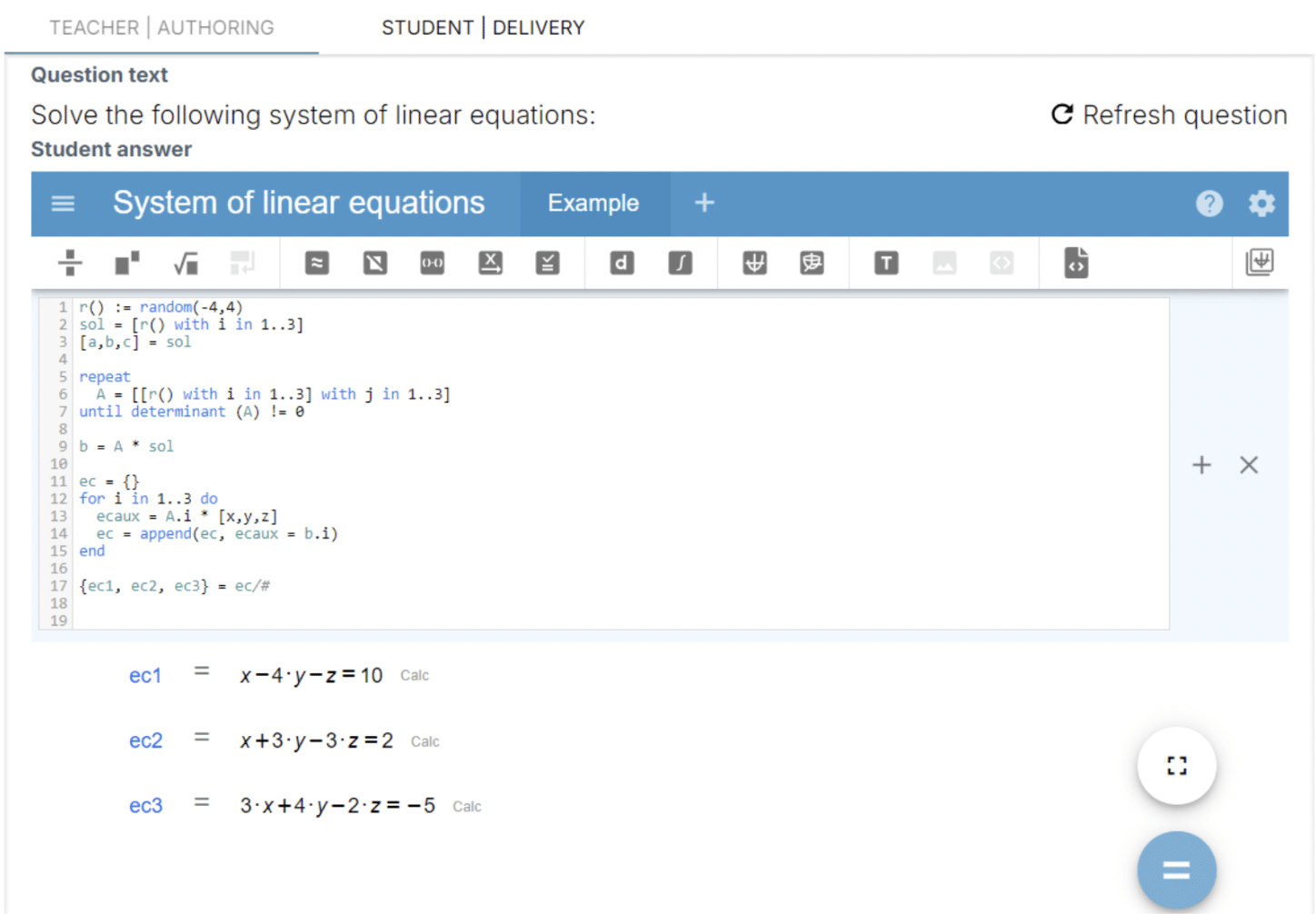
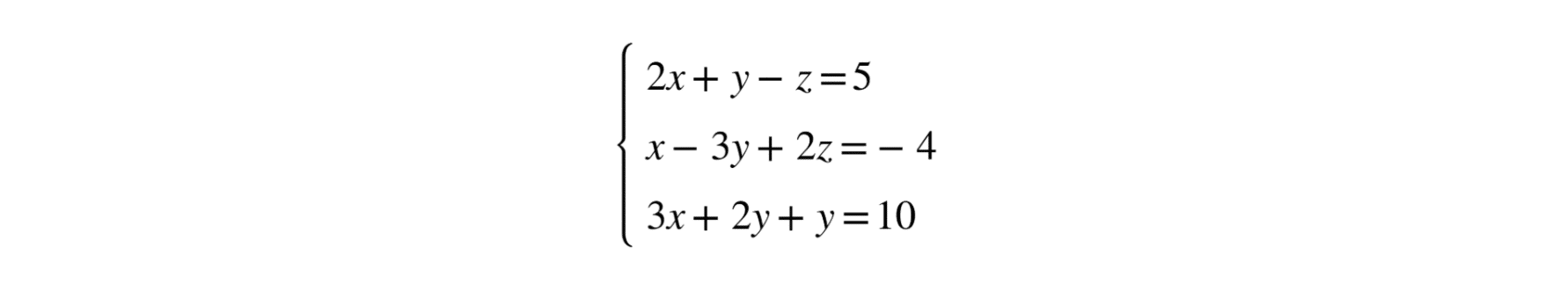Step-by-step Solution to an Oxford Access Exam Problem.

The Oxford University access exams are famous for their difficulty and for challenging students with mathematical problems of high complexity. In this article, we will focus on a 2020 exam problem that involves calculating the area between two curves. Through a clear and detailed analysis, we will break down each step necessary to approach and solve this mathematical challenge.

If you are interested, feel free to also visit our other article, “How to solve an equation of degree 16”, where we explore another challenging Oxford exam problem.

The problem statement is as follows:

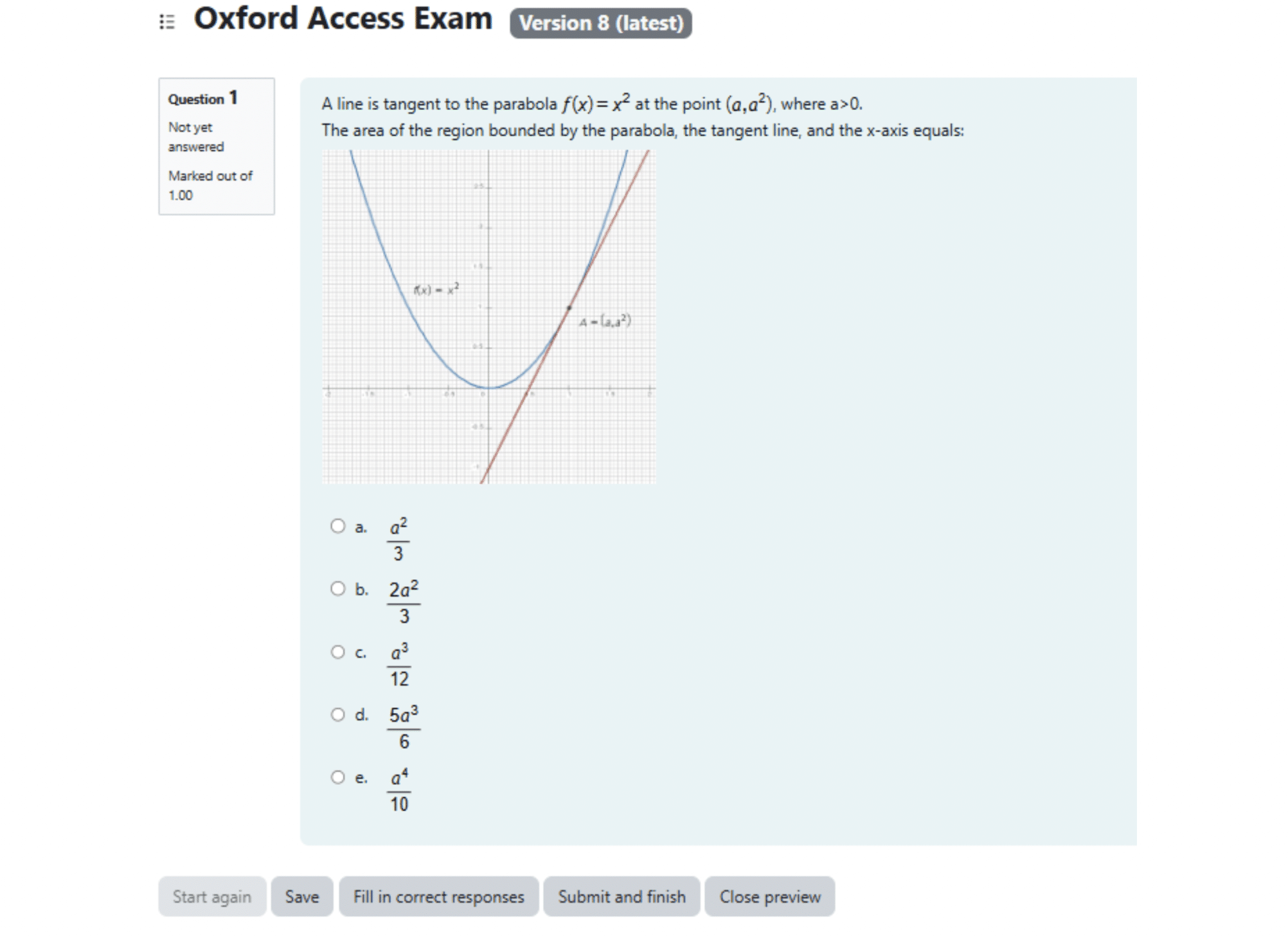
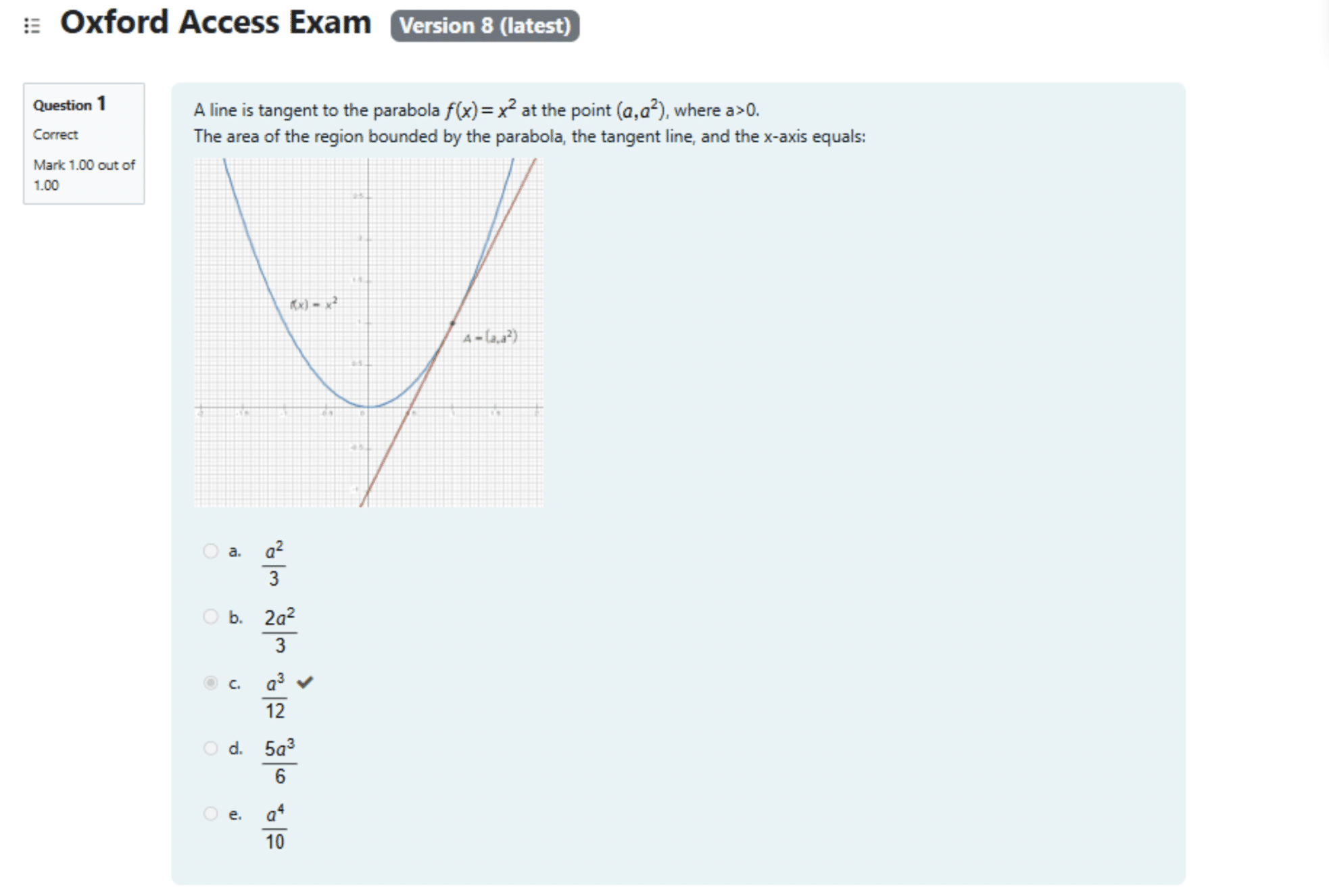
A line is tangent to the parabola y=x² at the point (a,a²), where a>0.

The area of the region bounded by the parabola, the tangent line, and the x-axis equals

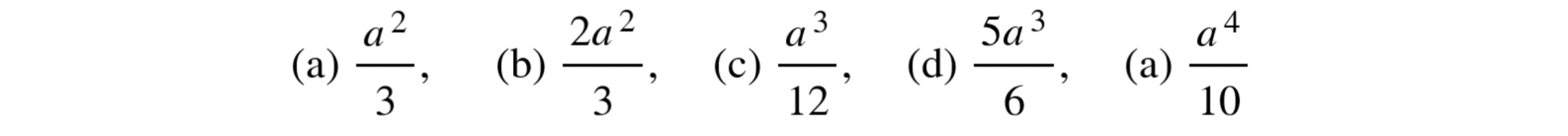
(a) a²⁄₃, (b) 2a²⁄₃, (c) a³⁄₁₂, (d) 5a³⁄₆, (a) a⁴⁄₁₀

This is a classic calculus problem that, as we will see, requires the use of both derivatives and integrals. Don’t worry; we’ll break it down into three clear and simple steps. Let’s get to it!

How to Find the Equation of the Tangent Line?

Before starting with the calculations, let’s visualize the problem. Below, you’ll see a graph illustrating the parabola y=x² and the tangent line at the point (a, a²), where a>0. In this graph, we can see how the tangent line touches the curve of the parabola at a single point without crossing it.

Now, to proceed, we first need to find the equation of the tangent line at that specific point. Since the tangent touches the parabola at point (a, a²), we need to determine both its slope and its equation.

This is where the derivatives come into play. The slope of the tangent at any point on the parabola is given by the derivative of the function y=x². We start by calculating the derivative: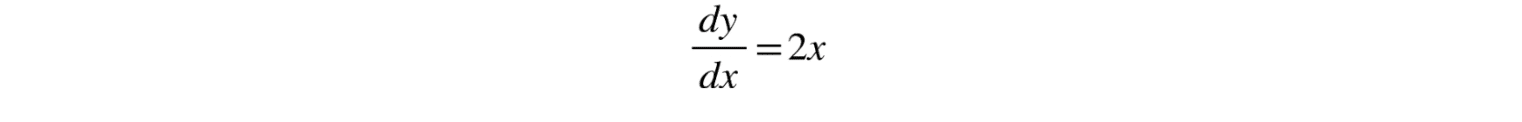 dy/dx=2x

This means that the slope of the tangent at any point on the parabola is 2x. To find the slope at the tangent point (a, a²), we substitute in the derivative:

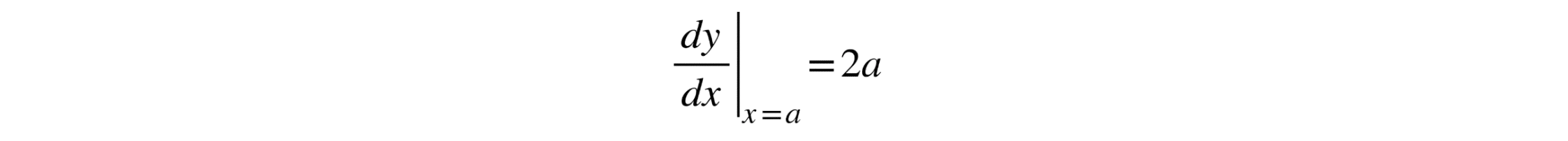
Therefore, the slope of the tangent line at point (a, a²) is 2a.

Now that we have the slope, we can write the equation of the tangent line using the formula for the line in its form:

y – y0 = m (x – x0)

Where m is the slope of the line, and (x0 , y0) is the point through which the line passes. In our case, the point of tangency is (a, a²), and the slope is 2a, so we substitute these values in the formula for the line:

y – a² = 2a (x-a)

y – a² = 2ax – 2a²

y = 2ax – a²

So, the equation of the tangent line at the point (a, a²) is:

y = 2ax – a²

Find the Intersection Points

Now that we have the equation of the tangent, we need to find the points of intersection between this tangent and the x-axis, that is, when y=0. This will allow us to determine the limits of the region whose area we want to calculate.

The area to be calculated is marked in orange in the graph below.

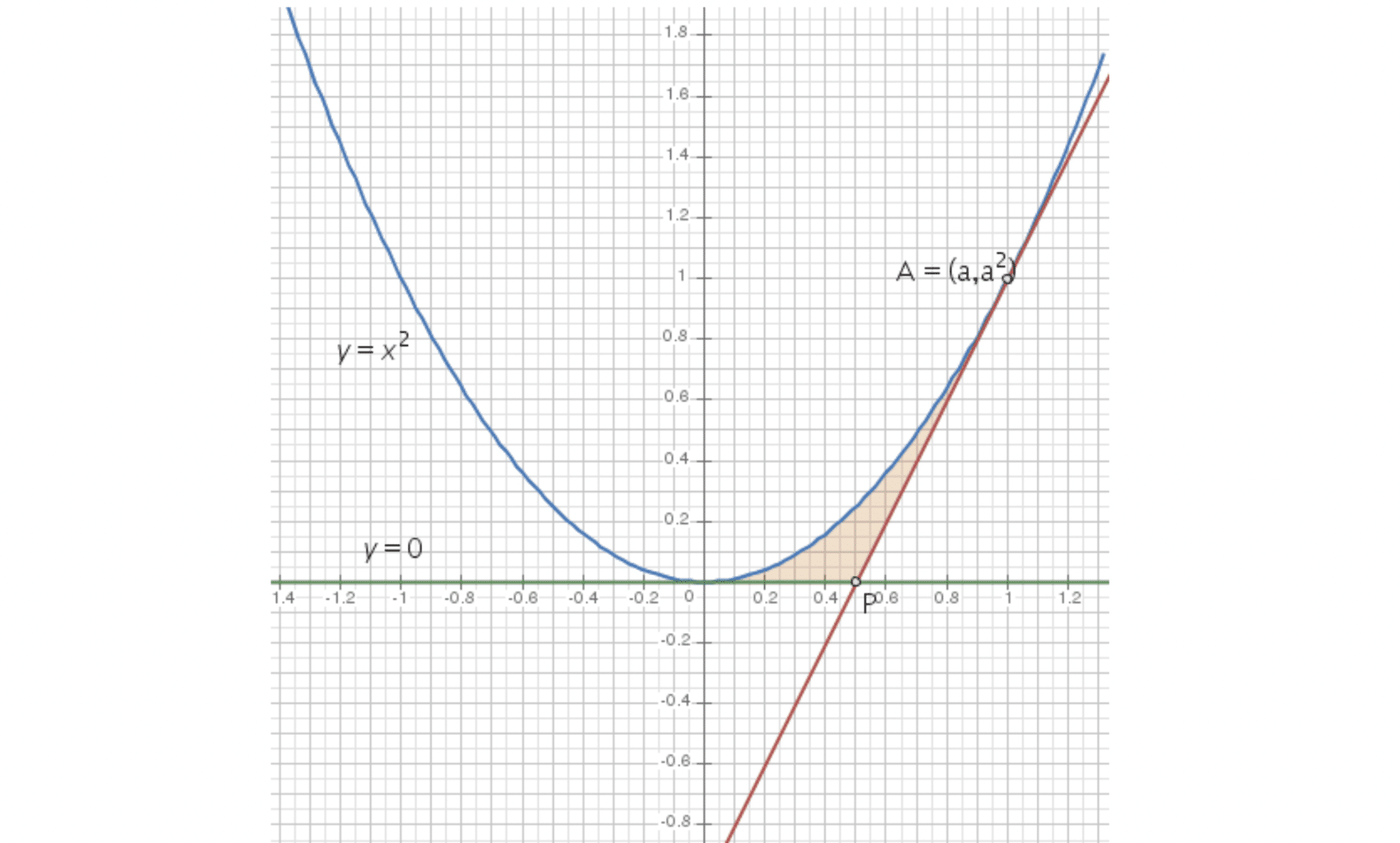
Substituting y=0 in the tangent equation and solving for x we obtain:

0= 2ax – a²

2ax = a²

x = a/2

So the tangent cuts the x-axis at point

P=(a/2, 0 )

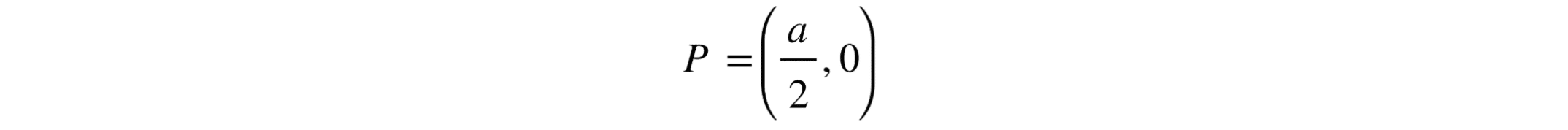
Calculate the Area Between the Parabola, the Tangent and the X-axis

Once we have the equation of the tangent and we know the points of intersection, we can proceed to calculate the area of the region bounded by the parabola, the tangent and the x-axis. For this, we use the definite integral, which allows us to find the area between two curves.

The area we want to calculate is obtained by subtracting two regions. In the first graph, you can see the total region we are interested in. However, part of this area is specifically delimited in the second graph, which we must subtract to be left with only the part we are looking for.

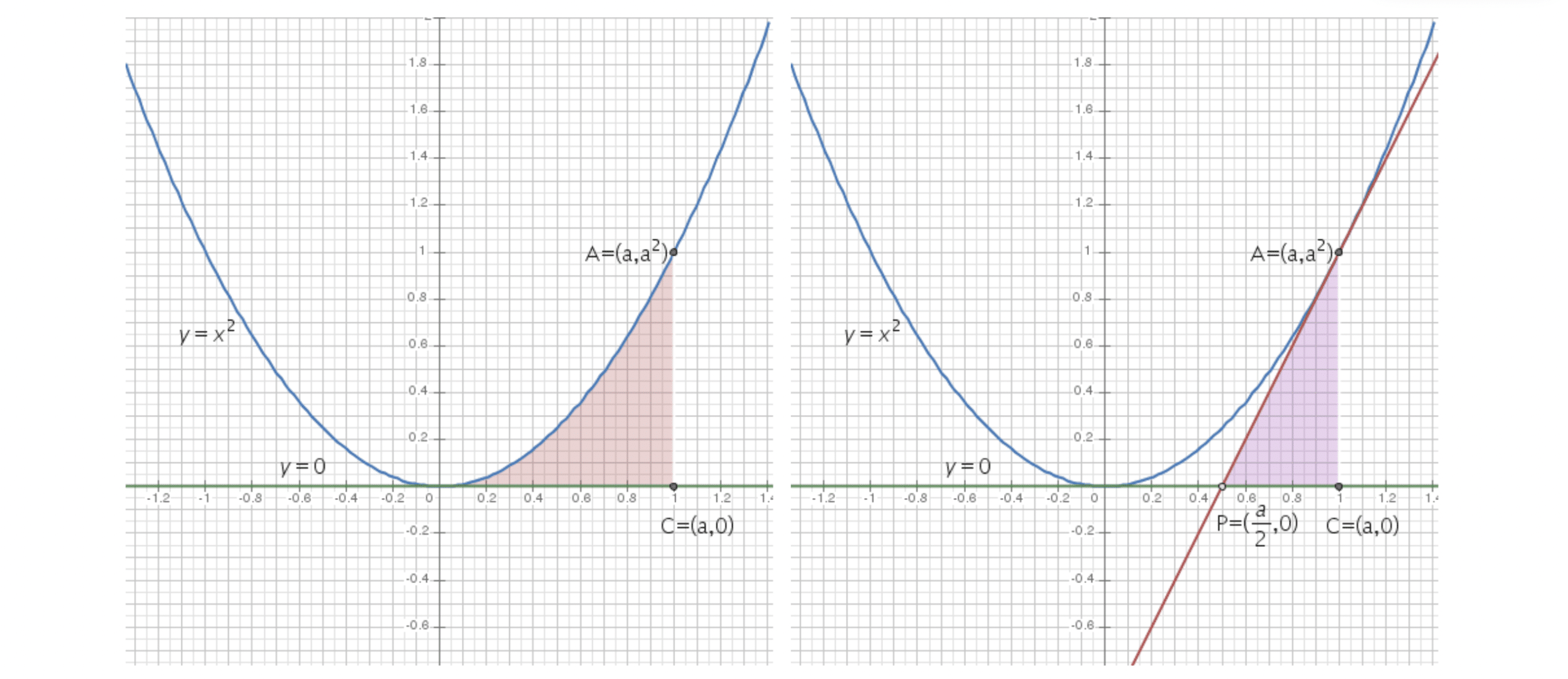
Let us calculate both integrals:  

a) Integral of graph 1:

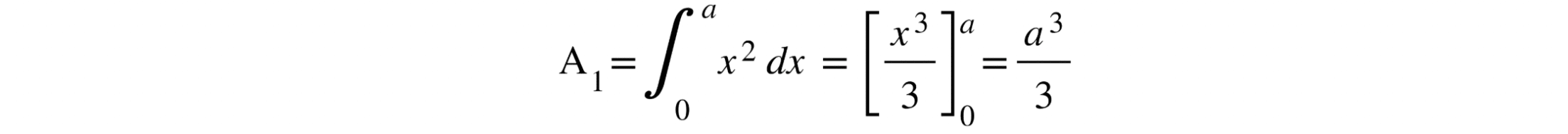
definite integral of x squared from 0 to a. It equals the integral from 0 to a of x squared dx, which is equal to x cubed over 3 evaluated from 0 to a, resulting in a cubed over 3.

b) Integral of graph 2:

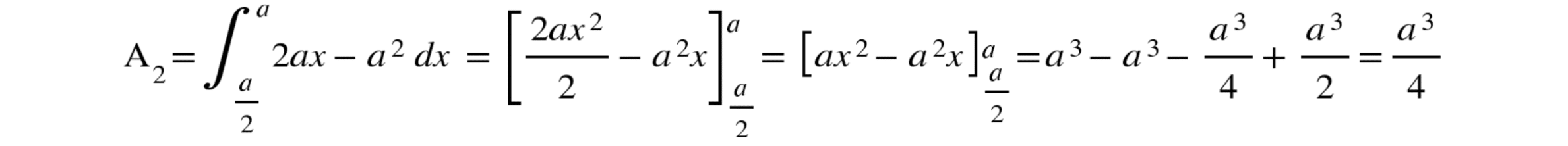
Now that we have solved all the integrals, we subtract the results to obtain the total area:

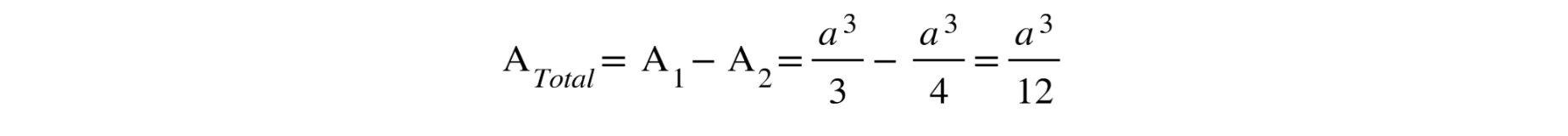
a total = a sub 1 - a sub 2 = a sup 3 / 3 - a sup 3 / 4 = a sup 3 / 12

In conclusion, the area of the region bounded by the parabola y = x², the tangent y = 2ax – a²  and the x-axis, is:

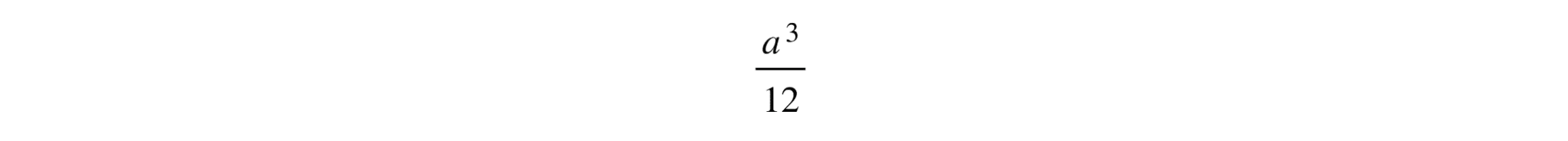
a sup 3 / 12

Therefore, option c is the correct answer

And so we come to the end of this fascinating problem! If you enjoyed this analysis or found it useful to better understand the solving process, feel free to share it with other math enthusiasts! 

Now we challenge you: do you dare to calculate the area formed by the curve y = x3 and its tangent at the point (1,1)? Share your solution or your ideas in the comments. We’d love to hear your approach!

Try WirisQuizzes to generate this exercise or others!

Categories
Uncategorized

Engaged Students, Better Results: La Salle’s Math Learning Platform With WirisQuizzes

From Textbooks to a Personalized Digital Math Learning Platform

When La Salle San Ildefonso set out to replace printed math textbooks with digital tools, they needed more than just online worksheets—they needed a complete math learning platform. With WirisQuizzes integrated into Moodle, their teachers built a collaborative system that supports independent learning, personalized feedback, and scalable assessment.

What started as one teacher’s initiative has become a model adopted across multiple La Salle campuses, reshaping how students engage with math.

The Challenge

When La Salle San Ildefonso first decided to phase out physical math textbooks, they faced a critical question: How do we offer high-quality math learning in a wholly digital format without sacrificing feedback, rigor, or accessibility?

As teacher Javier Melchior explained, early digital tools offered little beyond binary right-or-wrong grading

“The only feedback we could give was whether the answer was right or wrong. That wasn’t enough”, Javier explained. ”What students needed was guidance – not just the solution, but the how behind the solution”.

This insight became a turning point for La Salle’s approach to digital education. It wasn’t just about digitizing content but about ensuring that students could learn actively and reflectively within a new system.

At the same time, the shift to digital demanded a scalable infrastructure for:

  • Creating large volumes of exercises quickly.
  • Providing real-time, personalized feedback.
  • Supporting teachers across varying levels of technical proficiency.
  • Giving students the tools to practice independently and meaningfully.

Other platforms like Google Classroom, while helpful for document sharing, lacked the sophistication for in-depth math evaluation and formative feedback.

The Solution

That’s when WirisQuizzes came into focus—not just as a plugin but as the core engine behind La Salle’s custom-built math learning platform.

Led by Javier and math teacher Guillermo Pérez González, the department began building a shared bank of exercises directly within Moodle using WirisQuizzes. These weren’t just questions—they were intelligent, dynamic exercises that could offer step-by-step feedback, track partial understanding, and regenerate with different data for unlimited practice.

“We discovered the true power of WirisQuizzes when we realized we could break down a problem into parts,” said Javier. “It’s not just about getting the final answer. If a student does the first 20% right, the platform can recognize and score that.” 

WirisQuizzes became more than an assignment tool for students—it was their personal study assistant. “Now they ask us, ‘Is there a quiz for this topic?” Guillermo shared. “It’s become a natural part of how they study and prepare.”

The Implementation Process

La Salle’s implementation of WirisQuizzes was a grassroots initiative that grew into an institutional innovation. Here’s how it evolved.

Assessment

The shift began nearly a decade ago when La Salle removed printed textbooks for some math levels. With a digital-first model on the horizon, Javier started exploring alternatives. “I found WirisQuizzes online by chance,” he said. “And after testing its capabilities, I pitched it to my colleagues. From there, it just took off.”

Customization

Using Moodle’s system-level question bank, the teachers created hundreds of questions organized by topic: polynomials, functions, geometry, probability, and more. Every question included custom feedback. “Almost all our questions show the solution process,” said Javier. “This makes it easier for students to learn independently—even their parents can follow along.”

Importantly, this work was collaborative. Teachers built and reused each other’s content. “We never assigned categories formally,” said Guillermo. “If someone had free time, they’d jump in and add to the bank. It’s a shared resource for everyone.”

Deployment

WirisQuizzes was deployed through Moodle across the school. Teachers could:

  • Select questions from a shared bank.
  • Build quizzes quickly.
  • Offer time-limited assessments or practice exercises.
  • Use quizzes for classwork, homework, or even during substitute hours.

The school also exported question banks to other La Salle campuses in Tenerife, Madrid, and Gran Canaria. Adoption varied depending on each site’s IT support and teacher training, but the system was designed for easy export/import.

Training

While many core users were math or STEM teachers with programming experience, others found the “programming” aspect intimidating. Guillermo acknowledged this gap. “Some teachers hear ‘programming’ and think of C++,” he joked. “But it’s not like that. They’d see how simple it is if they just took one step.”

To address this, La Salle and Wiris discussed tailored training sessions that start simple, focusing on quiz-building basics before moving into more advanced logic and scripting.

The Results

La Salle’s math learning platform, powered by WirisQuizzes, delivered transformative results across several dimensions.

Improved Student Autonomy & Motivation

Students began voluntarily requesting quizzes to practice new topics. “It’s like they have a personal tutor,” said Javier. In one memorable example, he logged in on a weekend to find nine students had already completed a practice quiz and scored a perfect 10. “They were competing healthily. It became fun.”

Collaborative Efficiency Among Teachers

The math department created a bank of over 600–700 questions, reusable across grade levels and subjects. This significantly reduced prep time while increasing question quality and consistency.

Parental Engagement and Transparency

Because quizzes included feedback, parents could follow along, even if they weren’t strong in math. “Some told us they were thrilled to see their child working independently,” Guillermo shared.

Formative Assessment at Scale

Teachers used quizzes to diagnose student progress week by week. “In Bachillerato, I might run three quizzes weekly,” said Guillermo. “And they all count toward the grade. It keeps everyone working consistently.”

“WirisQuizzes isn’t just a quiz engine,” Javier added. “It’s a full feedback system. It’s the backbone of our math learning platform.”

The Future of WirisQuizzes at La Salle

La Salle continues to expand the use of WirisQuizzes beyond math:

  • They’ve developed questions for economics, technology, and even geography.
  • Some teachers are exploring how AI-based feedback could provide personalized remediation paths.
  • A growing number of educators across La Salle’s network are joining upcoming training sessions to learn how to build questions and customize feedback.

They’ve also expressed interest in exploring remote proctoring, integrating with other LMS platforms like Google Classroom, and co-developing content with other schools.

Rounding Off

La Salle’s transformation is a shining example of how a school can build its own collaborative, intelligent, and scalable math learning platform. By integrating WirisQuizzes into every level of instruction—from the classroom to home study—teachers empowered students with autonomy, parents with transparency, and the school with data-driven teaching strategies.

What started as one teacher’s experiment has become a system-wide initiative that is changing how La Salle teaches and how students learn.

👉 Want to build your own feedback-driven math platform?

Get in touch today

Categories
Uncategorized

Wiris in the Classroom: Learn and Practice with Unlimited Exercises

Learning mathematics requires more than just understanding theories: the key to mastering complex concepts and honing skills lies in continuous practice. However, traditional methods often limit the learning process: once the student has solved a problem, the challenge disappears, and exams often repeat the same questions, thus losing their value as an assessment tool. Imagine having the possibility to generate unlimited exercises with random variables, adapted to the needs of each student. With Wiris, this is now possible.

In addition, it has an automatic correction functionality which means that while the exercise is being generated, the answer is calculated simultaneously. This allows instant feedback, making it easier to learn and correct mistakes immediately.
For teachers, this tool offers a key advantage: the possibility of generating an infinite number of exercises, with each one being unique. In this way, teachers can create varied and personalized learning experiences, ensuring that students face new challenges every time they practice.

For their part, students enjoy constant practice which allows them to reinforce their skills without the worry of repeating the same exercises. In addition, this ability to generate unlimited exercises gives them excellent preparation for exams.

Practical example: Solving a system of linear equations

To illustrate how this tool works and how it can be used in the classroom, we will focus on solving systems of linear equations. We chose these types of problems because they represent a common mathematical challenge faced by all students and offer the possibility to explore different problem-solving methods. In addition, systems of equations can have various characteristics, such as being compatible, incompatible, or indeterminate, allowing students to work with a wide range of situations.

Let us imagine that we have the following system of linear equations with three unknowns:

We are going to solve it using Gauss’s Method. The first step is to write the system in the form of an augmented matrix: 

Now, we will apply elementary operations to reduce the matrix to its row echelon form.

Therefore, we obtain: 

From equation 3 of the system, we find the variable z:

Unlimited generation of systems of linear equations with random variables

Now that we have solved this system, for further practice, we would like to be able to generate new systems of equations of the same form but with random values.

These systems would take the following form:

Below, we will show you a code example to implement this functionality and generate given random systems of equations. With Wiris, it is totally possible!

r() := random(-4,4)

sol = [r() with i in 1..3]

[a,b,c] = sol

repeat 

A = [[r() with i in 1..3] with j in 1..3]

until determinant (A) != 0 

b = A * sol

ec = {}

for i in 1..3 do

ecaux = A.i * [x,y,z]

ec = append(ec, ecaux = b.i)

end

{ec1, ec2, ec3} = ec

r() := random(-4,4): This function generates a random number between -4 and 4.

sol = [r() with i in 1..3]: Here, three random values are generated that will represent the solutions of the system of equations.

[a,b,c] = sol: The generated values are assigned to the unknowns of the system.

repeat…until determinant(A) != 0: This block ensures that the coefficient matrix A is invertible (i.e., its determinant is not zero), which guarantees the system has a unique solution.

b = A * sol: The result vector b is calculated by multiplying the coefficient matrix A by the solutions sol

for i in 1..3 do: In this cycle, the three equations are generated, using each of the rows of the matrix A and the solutions sol.

{ec1, ec2, ec3} = ec: Finally, the three generated equations are stored in the variables ec1, ec2, and ec3, ready to be used in new exercises.

Using WirisQuizzes and implementing this code as a question, we can obtain the following results:

Reloading another system with the symbol “=” generates a new set of equations, as shown below:

For more details, you can consult the complete product documentation here.

If you have found this article useful, we would love you to share it with other colleagues, teachers or students. We would also be delighted to hear your opinion and any suggestions you may have.

 

Check Out WirisQuizzes

Categories
Uncategorized

Instant Feedback in Open-Ended Math Questions: Key Takeaways from BETT 2025

Bett congress 2025 Wiris Tech in Action

Recently, we had the exciting opportunity to showcase our approach at BETT 2025: Enhancing Open-Ended Math Questions with Instant Feedback to teachers, publishers and educators alike at the conference in London. Feedback plays a crucial role in guiding learning, and at the event, we focused on how instant feedback in open-ended math questions can dramatically enhance students’ mathematical understanding, all the while assisting teachers and making their day to day more efficient.

Unlike traditional multiple-choice problems, open-ended mathematics questions require deeper thinking as they are questions that a student can freely answer without a predefined format, making personalized feedback more vital. In this article, we will explore the significance of instant feedback in open-ended math questions and discuss how different types of feedback—corrective feedback, confirmatory feedback, and suggestive feedback—can help students improve.

 

 

Why Instant Feedback Matters in Open-Ended Math Questions

The Power of Feedback in the Learning Process

Feedback is integral to the learning process, helping students refine their thinking and improve their understanding. This is especially true for open-ended mathematics questions, where there is often no one right answer. In such cases, instant feedback in open-ended math questions can make a significant difference in guiding students toward the correct solution.

During BETT 2025, we discussed how instant feedback in math questions not only helps students correct mistakes quickly and builds their confidence but how it also assists teachers in the class environment making the teaching and learning process much more efficient.

 

Types of Feedback for Open-Ended Math Questions

Different types of feedback are required depending on the student’s needs and the nature of the question. The three main types of feedback we focused on at BETT 2025 are suggestive feedback, confirmatory feedback, and corrective feedback.

Suggestive Feedback in Math Questions

Suggestive feedback in math questions guides students to discover the solution themselves. Instead of providing the correct answer outright, suggestive feedback encourages independent problem-solving. For example, if a student suggests “2 and 8” as the two numbers whose sum is 10 and product is maximum, suggestive feedback might be: “What happens if you try numbers closer together?”

 

Confirmatory Feedback in Math Questions

Confirmatory feedback in math questions is designed to reinforce correct answers. When students solve problems correctly, feedback like “That’s correct, well done!” helps to affirm their understanding and boosts their confidence.

In the case of open-ended math questions, confirmatory feedback is invaluable for ensuring students stay motivated, especially when they are tackling complex problems.

This type of feedback fosters critical thinking and encourages exploration, making it an essential tool for developing problem-solving skills in open-ended math questions.

 

Corrective Feedback in Math Questions

Corrective feedback in math questions identifies mistakes and provides the correct answer. For example, if a student incorrectly solves x^2=4 as x=4, the corrective feedback would be “The correct solution is x= +-2”.

While effective for addressing misunderstandings, corrective feedback should be used in moderation, as over-reliance on it can hinder the development of problem-solving skills.

 

 

The Teaching Cycle: A Framework for Feedback Application

At BETT 2025, Mrs. Brook, a fictional high school math teacher, shared her teaching cycle, which integrates corrective, suggestive, and confirmatory feedback seamlessly. Her cycle is designed to maximize learning outcomes by aligning feedback strategies with the different stages of teaching.

The Four Stages of Mrs. Brook’s Teaching Cycle

  • Delivering the Content

Mrs. Brook begins her teaching by introducing and explaining the content to her students. This step ensures all students have a baseline understanding of the topic.

  • End-of-Class Knowledge Validation

Following the lesson, Mrs. Brook conducts an end-of-class knowledge check. This is where corrective feedback plays a crucial role. For example, if a student misunderstands a concept or calculation, Mrs. Brook provides immediate corrective feedback to clarify misconceptions.

 

  • Recommending Practice at Home

Mrs. Brook encourages her students to practice independently. At this stage, she often employs suggestive feedback to guide students without directly giving them answers, helping them to think critically and explore solutions. Additionally, confirmatory feedback is used to reinforce correct solutions and build student confidence. When students solve problems accurately, Mrs. Brook provides positive reinforcement such as “Great job!” to motivate them and affirm their understanding.

 

  • Assessing Students’ Knowledge Levels

After students have had the opportunity to practice, Mrs. Brook assesses their progress to identify areas of improvement. During this phase, she focuses on encouraging students to reflect on their learning journey and strive for continued growth. She fosters a positive environment by recognizing their efforts and offering motivation to help them stay engaged and confident in their abilities.

This cyclical model of teaching and feedback showcases how structured feedback enhances learning and ensures students’ needs are addressed at every stage​Tech.

 

 

Wrapping up: Embracing the Future of Math Education with Wiris

At WIRIS, we’re committed to supporting educators with the tools they need to provide effective feedback. Our Learning Lemur and WirisQuizzes products ensure that instant feedback in open-ended math questions is accessible and customizable, helping students succeed in their math learning journey.

As technology continues to evolve, the integration of instant feedback into open-ended math questions will only become more critical. We look forward to the continued evolution of math education, driven by personalized learning and real-time feedback.

Unlock Instant Feedback Today

 

Making people’s STEM work more meaningful