Post type: Company

Categories
Uncategorized

MathType Math Equation Writer Joins the Skolon Educational App Store

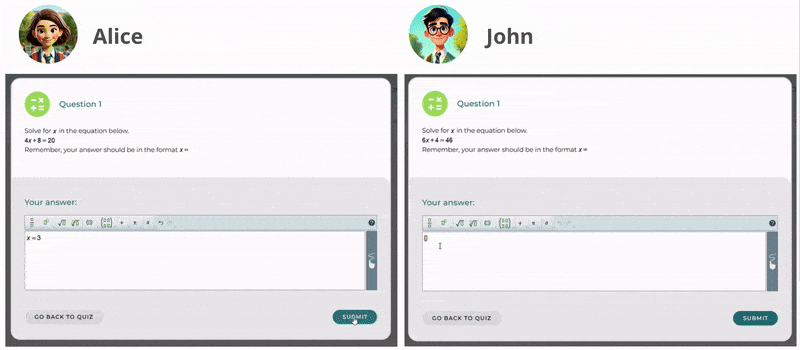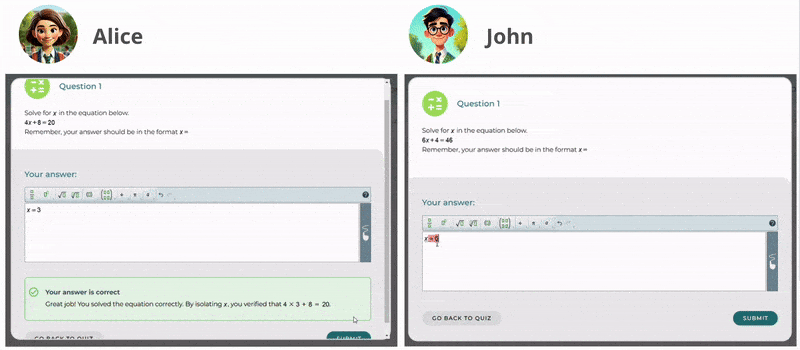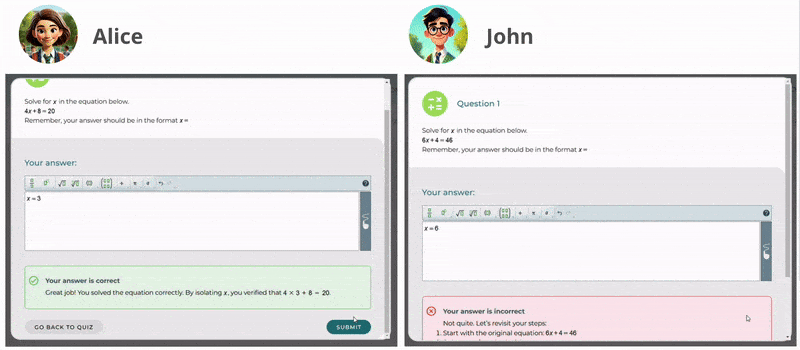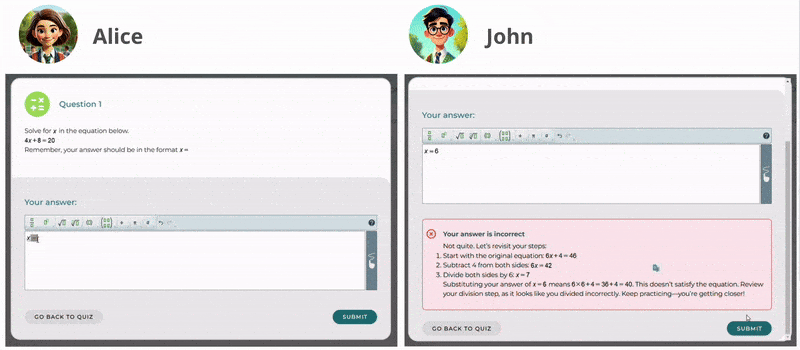
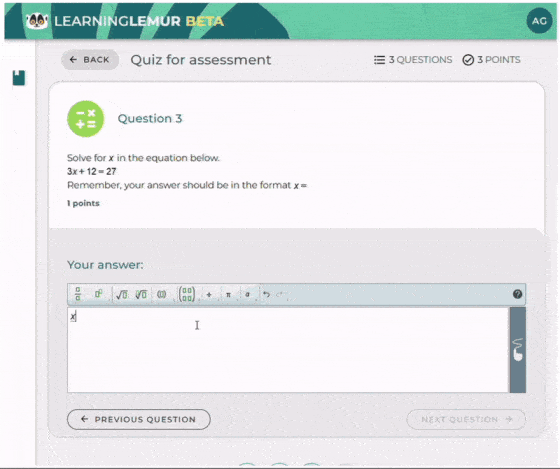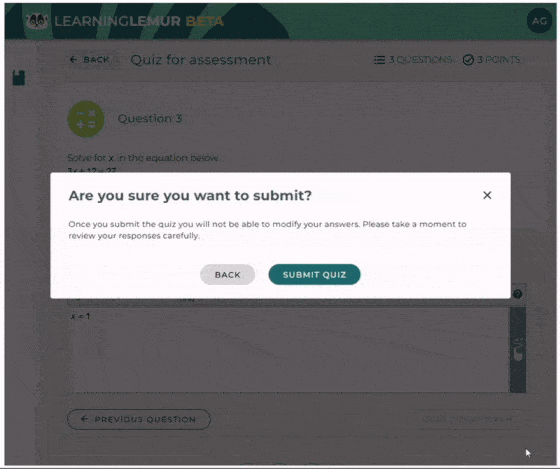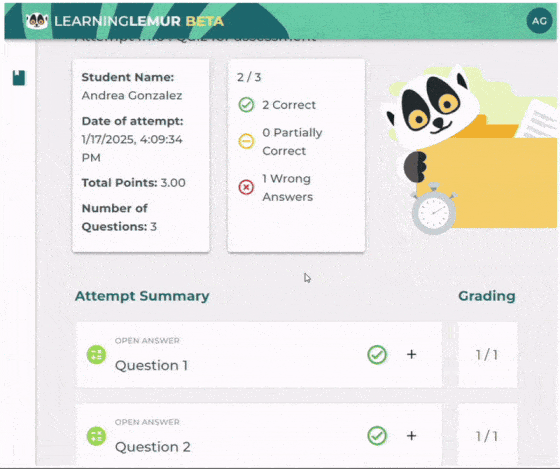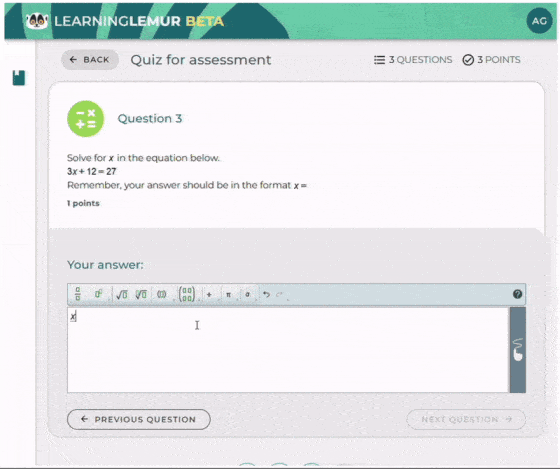
A New Chapter for MathType: Now on Skolon

Wiris is thrilled to announce that MathType, our renowned math equation writer for creating and editing math equations, is now available on Skolon’s educational App Store. This partnership marks a significant milestone in our mission to simplify mathematical education for students and teachers worldwide. With features that enhance math content formatting, MathType improves how math expressions are presented and understood in digital learning environments.

What Does This Mean for Educators and Students?

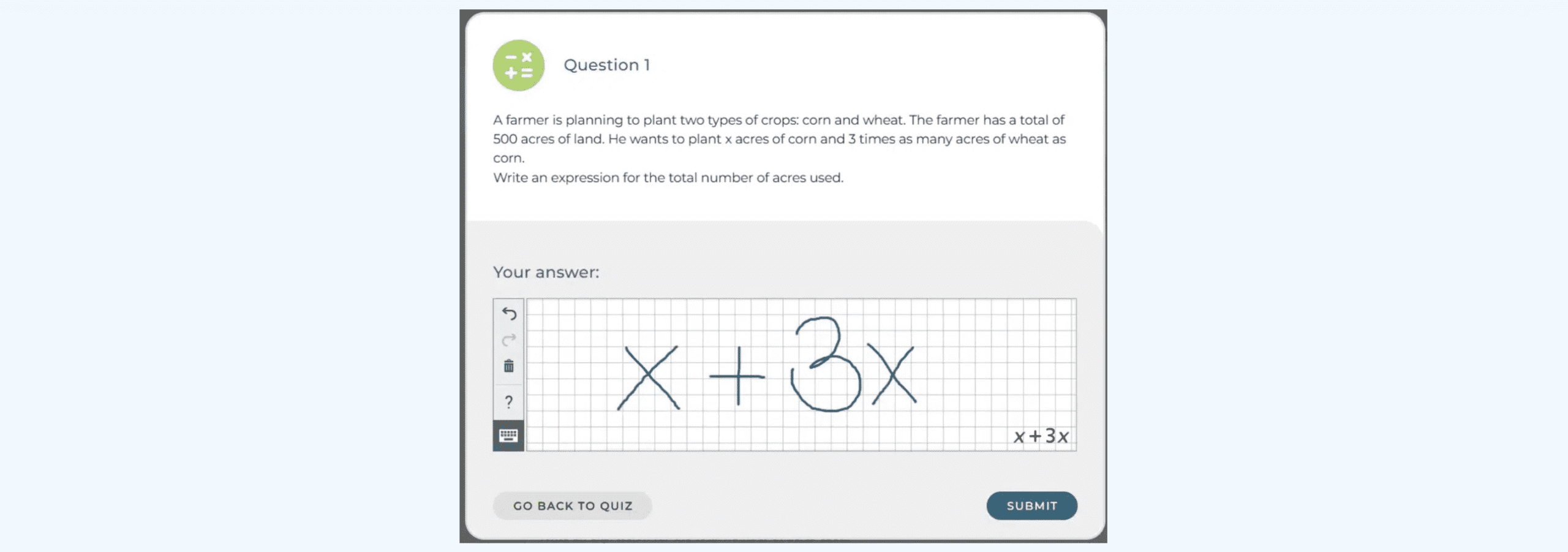
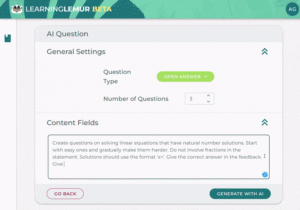
Through Skolon’s platform, educators can seamlessly integrate MathType’s equation editor into their teaching resources. With its intuitive interface and powerful features, MathType makes it easier than ever to create professional-quality math equations and notations. For students, this tool provides an accessible way to engage with complex mathematics, fostering a deeper understanding of the subject. Additionally, its formatting tools ensure that mathematical expressions remain clear and well-structured in different digital contexts.

Why Choose MathType Math Equation Writer on Skolon?

By joining forces with Skolon, we ensure that educators and students gain easy access to MathType’s math equation writer’s capabilities. Skolon’s platform simplifies the process of discovering, purchasing, and deploying educational tools, making it an ideal partner for delivering MathType’s benefits to a wider audience. Now, schools can quickly adopt MathType as part of their digital learning ecosystem, streamlining both teaching and learning experiences. With enhanced formatting and compatibility features, MathType further improves the clarity of mathematical content across multiple formats.

About Skolon’s Educational App Store

Skolon is a trusted name in the education technology space in Northern Europe, offering a comprehensive App Store that caters to the diverse needs of schools and educators. Their platform enables users to access and manage a wide range of digital tools in one convenient location, and we’re proud to see MathType’s math equation writer among their trusted offerings. The ability to generate clear and structured mathematical expressions ensures that digital math content remains visually precise and easily shareable.

Get Started with MathType Today

We invite you to explore MathType on Skolon and experience firsthand how its math equation writer can enhance your educational efforts. Whether you’re a teacher aiming to enrich your curriculum or a student looking for a better way to approach mathematics, MathType on Skolon is here to support you. With advanced formatting options, MathType ensures mathematical clarity across digital platforms.

Discover MathType on Skolon Now

Looking Ahead

At Wiris, we’re committed to empowering the education sector through innovative tools like MathType. Partnering with Skolon brings us closer to our goal of making math accessible, engaging, and enjoyable for everyone. By leveraging MathType’s math equation writer and its enhanced presentation features, we continue to enhance digital learning worldwide.

Stay tuned for more updates as we continue to expand our reach and improve learning experiences globally.

Categories
Uncategorized

How to solve an equation of degree 16

Step-by-step solution of an Oxford access exam problem

Every year, thousands of students face the challenge of the admission exams to enter the prestigious University of Oxford, a process that tests not only their knowledge, but also their ability to solve under pressure. In particular, the math exam is known for its complexity, posing problems of all kinds, from solving equations to questions of logic, advanced algebra, calculus and number theory. In this article, we will explore one of the problems presented in October 2023. 

The problem poses the following question: how many real solutions does the following equation have?

Do you dare to solve the equation before reading the complete solution in the blog? 

At first glance, the statement seems simple: an equation with a single variable, where all the numbers involved are integers between 1 and 4. However, the real difficulty lies in correctly undoing the squared parentheses, making sure to consider all possible cases. 

A key detail in this type of equations is that, when squaring a number, the same result is obtained for both its positive and negative values. For example: 

This occurs because squaring a number eliminates the negative sign. Therefore, when solving a quadratic equation we must take into account the two possible options: the positive and the negative number that can generate that result. 

One last observation: if we were to fully develop the parentheses, we would obtain an equation of the form xˆ16+…, which indicates that the equation is of degree 16 and, at most, could have 16 real solutions for x. Therefore, we cannot rule out any of the options presented to us as possible answers.

Since for equations of degree 16 there is no systematic formula like Ruffini’s method for polynomials of degree 3, we will solve this equation by working the parentheses progressively, from the outermost to the innermost.

 

Specific example of how to solve an equation of degree 16

Let’s get on it! 

Let’s start with the outermost parenthesis. If we define t as ((x²-1)²-2)²-3 , then we get t²=4. This gives us two possible values for t: t=2 or t=-2. 

Substituting t by its original value in each case, we obtain the following results: 

1. If t=2 then: ((x²-1)²-2)²-3 =2 ⇒ ((x²-1)²-2)²=5 and again, substituting r= (x²-1)²-2 we obtain that r²=5 . Let’s look at the two new cases that arise:

1.1 r=√5: substituting r for its original value we obtain (x²-1)²-2 =√5 ⇒ (x²-1)²=2+√5 and again, one last time, we substitute s=x²-1, we obtain that s²=2+√5 and observe the two results again:

When trying to calculate the square root to obtain the value of x, we would be taking the root of a negative number. As a result, the two values obtained will be imaginary numbers.

1.2 r=-√5 substituting r for its original value we obtain (x²-1)²-2=-√5 ⇒ (x²-1)²=2-√5 . Following the same reasoning as in the previous section, given that √4=2, it follows that √5>2 . This implies that 2-√5<0, and when trying to calculate its square root, we would obtain an imaginary number. Therefore, when we continue developing to obtain the value of x, this would also be an imaginary number.

2. If t=-2 then: ((x²-1)²-2)²-3 =-2 ⇒ ((x²-1)²-2)²=1 and again, substituting r= (x²-1)²-2 we obtain that r²=1 . Let’s look at the two cases:

2.1 r=1: substituting r for its original value we obtain (x²-1)²-2 =1 ⇒ (x²-1)²=3 and again, one last time, we substitute s=x²-1, we obtain that s²=3 and observe the two results again:

2.1.1 s=√3 and substituting s for its value, we finally obtain: x²-1=√3 ⇒ x²=1+√3 and therefore

2.1.2 s=-√3 substituting s for its original value we obtain x²-1=-√3 ⇒ x²=1-√3 . This subtraction is negative, since √2≈1,41 and therefore, √3>1,41 with which we deduce that 1-√3<0 , and when trying to calculate its square root, we would obtain an imaginary number.

2.2 r=-1 substituting r for its original value we obtain (x²-1)²-2 = -1 ⇒ (x²-1)² = 1 and again, one last time, we substitute s=x²-1 and we obtain that s²=1 and observe the two results again:

2.2.1 s=1 and substituting s for its value, we finally obtain: x²-1 = 1 ⇒ x²=2 and therefore

2.2.1.1 x=√2 which is a real solution.

2.2.1.2 x=-√2 which is a real solution.

2.2.2 s=-1 and substituting s for its value, we finally obtain: x²-1 = -1 ⇒ x²=0 and therefore the only possible solution is x=0 .

Let’s review all the possible real values we have obtained:

 

This gives us a total of 7 real solutions for x, so the correct answer is option (c).

Did you get your answer right?

Drawing this equation with our graphing tool is a simple and effective way to check the number of real solutions. Looking at the graph, you can clearly see how the curve interacts with the x-axis, confirming the previous result. Below, we show you the graph to see for yourself:

Done with the WirisQuizzes Assessment tool

 

Will you dare to take on more challenges in the future?

If you found this content useful or inspiring, please share it with your friends and fellow number lovers!

Categories
Uncategorized

Instant Feedback in Open-Ended Math Questions: Key Takeaways from BETT 2025

Bett congress 2025 Wiris Tech in Action

Recently, we had the exciting opportunity to showcase our approach at BETT 2025: Enhancing Open-Ended Math Questions with Instant Feedback to teachers, publishers and educators alike at the conference in London. Feedback plays a crucial role in guiding learning, and at the event, we focused on how instant feedback in open-ended math questions can dramatically enhance students’ mathematical understanding, all the while assisting teachers and making their day to day more efficient.

Unlike traditional multiple-choice problems, open-ended mathematics questions require deeper thinking as they are questions that a student can freely answer without a predefined format, making personalized feedback more vital. In this article, we will explore the significance of instant feedback in open-ended math questions and discuss how different types of feedback—corrective feedback, confirmatory feedback, and suggestive feedback—can help students improve.

 

 

Why Instant Feedback Matters in Open-Ended Math Questions

The Power of Feedback in the Learning Process

Feedback is integral to the learning process, helping students refine their thinking and improve their understanding. This is especially true for open-ended mathematics questions, where there is often no one right answer. In such cases, instant feedback in open-ended math questions can make a significant difference in guiding students toward the correct solution.

During BETT 2025, we discussed how instant feedback in math questions not only helps students correct mistakes quickly and builds their confidence but how it also assists teachers in the class environment making the teaching and learning process much more efficient.

 

Types of Feedback for Open-Ended Math Questions

Different types of feedback are required depending on the student’s needs and the nature of the question. The three main types of feedback we focused on at BETT 2025 are suggestive feedback, confirmatory feedback, and corrective feedback.

Suggestive Feedback in Math Questions

Suggestive feedback in math questions guides students to discover the solution themselves. Instead of providing the correct answer outright, suggestive feedback encourages independent problem-solving. For example, if a student suggests “2 and 8” as the two numbers whose sum is 10 and product is maximum, suggestive feedback might be: “What happens if you try numbers closer together?”

 

Confirmatory Feedback in Math Questions

Confirmatory feedback in math questions is designed to reinforce correct answers. When students solve problems correctly, feedback like “That’s correct, well done!” helps to affirm their understanding and boosts their confidence.

In the case of open-ended math questions, confirmatory feedback is invaluable for ensuring students stay motivated, especially when they are tackling complex problems.

This type of feedback fosters critical thinking and encourages exploration, making it an essential tool for developing problem-solving skills in open-ended math questions.

 

Corrective Feedback in Math Questions

Corrective feedback in math questions identifies mistakes and provides the correct answer. For example, if a student incorrectly solves x^2=4 as x=4, the corrective feedback would be “The correct solution is x= +-2”.

While effective for addressing misunderstandings, corrective feedback should be used in moderation, as over-reliance on it can hinder the development of problem-solving skills.

 

 

The Teaching Cycle: A Framework for Feedback Application

At BETT 2025, Mrs. Brook, a fictional high school math teacher, shared her teaching cycle, which integrates corrective, suggestive, and confirmatory feedback seamlessly. Her cycle is designed to maximize learning outcomes by aligning feedback strategies with the different stages of teaching.

The Four Stages of Mrs. Brook’s Teaching Cycle

  • Delivering the Content

Mrs. Brook begins her teaching by introducing and explaining the content to her students. This step ensures all students have a baseline understanding of the topic.

  • End-of-Class Knowledge Validation

Following the lesson, Mrs. Brook conducts an end-of-class knowledge check. This is where corrective feedback plays a crucial role. For example, if a student misunderstands a concept or calculation, Mrs. Brook provides immediate corrective feedback to clarify misconceptions.

 

  • Recommending Practice at Home

Mrs. Brook encourages her students to practice independently. At this stage, she often employs suggestive feedback to guide students without directly giving them answers, helping them to think critically and explore solutions. Additionally, confirmatory feedback is used to reinforce correct solutions and build student confidence. When students solve problems accurately, Mrs. Brook provides positive reinforcement such as “Great job!” to motivate them and affirm their understanding.

 

  • Assessing Students’ Knowledge Levels

After students have had the opportunity to practice, Mrs. Brook assesses their progress to identify areas of improvement. During this phase, she focuses on encouraging students to reflect on their learning journey and strive for continued growth. She fosters a positive environment by recognizing their efforts and offering motivation to help them stay engaged and confident in their abilities.

This cyclical model of teaching and feedback showcases how structured feedback enhances learning and ensures students’ needs are addressed at every stage​Tech.

 

 

Wrapping up: Embracing the Future of Math Education with Wiris

At WIRIS, we’re committed to supporting educators with the tools they need to provide effective feedback. Our Learning Lemur and WirisQuizzes products ensure that instant feedback in open-ended math questions is accessible and customizable, helping students succeed in their math learning journey.

As technology continues to evolve, the integration of instant feedback into open-ended math questions will only become more critical. We look forward to the continued evolution of math education, driven by personalized learning and real-time feedback.

Unlock Instant Feedback Today

 

Categories
Uncategorized

Wiris’ New Partnership with Moodle

Hands shaking partner Skolon

MathType, the New Moodle’s Certified Integration Partner

Wiris is pleased to announce our new strategic partnership with Moodle. Wiris has earned the title of Moodle’s Certified Integration Partner by offering MathType, a powerful and reliable add-on that elevates the quality of the online learning experience. This integration meets exacting technical standards and security requirements, addressing real-world educational needs.

With MathType, Moodle users can easily create and edit mathematical equations and formulas directly within the platform. It allows the inclusion of math expressions and formulas into assignments, questions, or communications between users. Whether users prefer the intuitive toolbar or the touch screen capabilities with handwriting recognition, MathType offers versatile methods for expressing mathematical concepts within the Moodle environment.

This partnership will benefit both companies, streamlining the process of selecting and integrating the necessary tools to extend Moodle’s functionality. It provides the assurance of tools that have demonstrated compliance with rigorous technical standards and security requisites, ultimately enhancing the learning experience for our users with user-tested, endorsed integrations. 

“Our solutions have been integrated with Moodle for over 15 years. As we continue to collaborate closely with Moodle, we’re inspired by the positive impact our joint efforts will have on students and educators worldwide,” says Ramon Eixarch, CEO and Co-Founder of Wiris.

At Wiris, we are excited about this new chapter, enthusiastic to further enhance our services, and deeply appreciative of the confidence placed in us.

Sources:

Categories
Uncategorized

Creating accessible STEM content

Wheelchair optimized Accessibility program

Wiris pushes against the lack of accessible STEM content. 

Our platform uses the MathML standard to be accessible for everybody.

One of the biggest obstacles for the educational community is the lack of accessible STEM content as well as the absence of adequate tools to create said materials. STEM is the acronym of Science, Technology, Engineering and Mathematics, an area of education specialized in interdisciplinarity and application of science and mathematics.

STEM content accessible for people with vision impairments are not common. Although nowadays there are many tools to generate accessible materials, the problem lies in the few options available  for the creation of accessible and adequate resources for STEM classes. This creates many obstacles for disabled Stem professionals to make their content available for everyone.

Luckily there are successful initiatives that mitigate this problem. Wiris has built MathType in a way that is totally navigable with the keyboard and fully compatible with the majority of the screen-readers in the market, which allow people with visual impairments to be guided by an off-voice. Thus, Wiris makes sure its products are accessible to everybody.

These accessibility options work for both the process of creating STEM content, and of using and working with it. Besides, WirisQuizzes is also built so that the students can answer exam questions in a fully accessible and autonomous way.

 

Available for your computer and on-line.

MathType works both for the desktop framework(text editors), and for on-line services(Google services and most LMS platforms), thus making it the most advanced mathematical authoring tool in the market. MathType can achieve this goal by automatically adding alternative text to the created equations, adding it in the HTML code when you are working in a web platform, or to the images when you work with the desktop app.

In addition, all Wiris products are based on the MathML standard, a coding language that incorporates both the structure and the content of the mathematical expression. Many screen-readers are equipped with MathML format reading capability, which makes Wiris accessible in the majority of devices. Moreover, the MathML language has many features that make it very useful for people with disabilities. 

For its ease of navigation with the keyboard and its use of the MathML language, MathType has created a new accessibility standard in mathematical tools both for students and professionals.

Sources:

Categories
Uncategorized

Wiris stands with Ukraine

Raised Hand for Ukraine

From Wiris, we would like to express our deep concern about the situation in Ukraine, and join so many voices from around the world in calling for peace. We stand with all the people who are suffering at this moment and condemn the use of any military action. 

Wiris joins the firm condemnation against the war in Ukraine made by the ACUP (Catalan Association of Public Universities).

For this, we have made the decision to provide all Ukraine accounts with free MathType licenses until the 20th of September 2022.

Please contact support@wiris.com if you have been affected by this conflict and wish to receive a free license.

Making people’s STEM work more meaningful