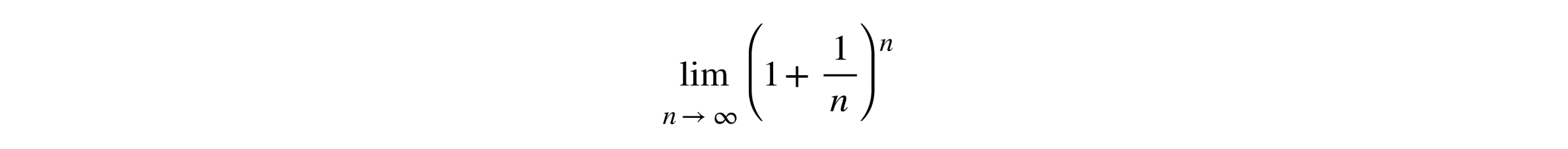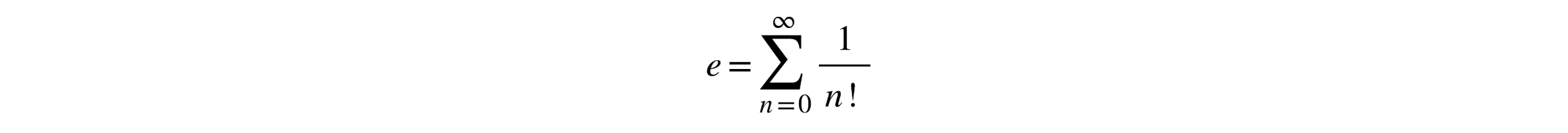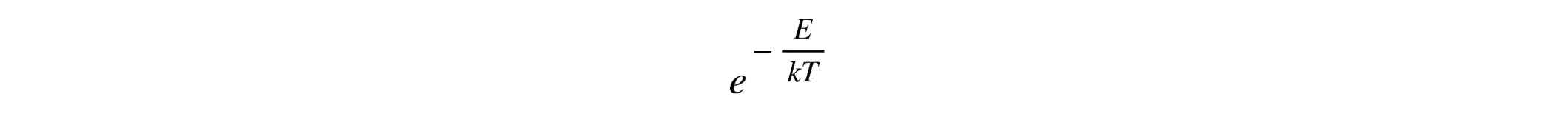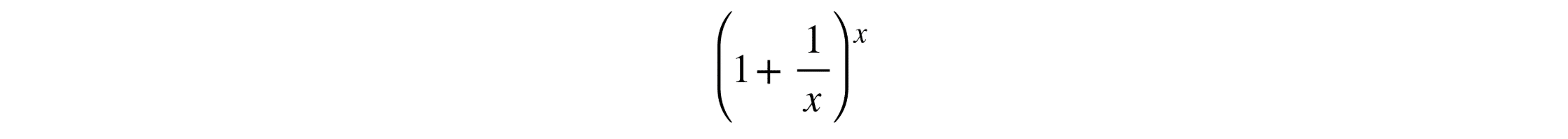Year: 2025

Driving Innovation in Math Assessment Tools: How ASSISTments Uses MathType

Post author By Aida Alsina
Post date September 23, 2025

Transforming Digital Math Content in Real Classrooms

In the fast-paced world of digital math content, precision and clarity are vital for effective learning. ASSISTments, a free online math platform for grades 3-12, empowers teachers to assign math problems and provide students with instant feedback. With thousands of students and educators relying on the platform every day, ASSISTments needed a scalable, accurate, and accessible solution to handle complex mathematical notation. Here enters MathType, the tool that powers math expressions in both content creation and student responses within their math assessment tools.

When Equations Were Messy: The Challenges Before MathType

As an assessment platform, ASSISTments faced growing demands around consistency in math content creation and clarity of expression. According to Ryan Emberling, Director of Engineering at the ASSISTments Foundation, one of their biggest pain points was formatting:

“It was a pain point for students to type things like sqrt() to express their answers, and for teachers to make sense of those submissions.”

Generating and interpreting math notation without a standardized editor led to confusion and inefficiency.

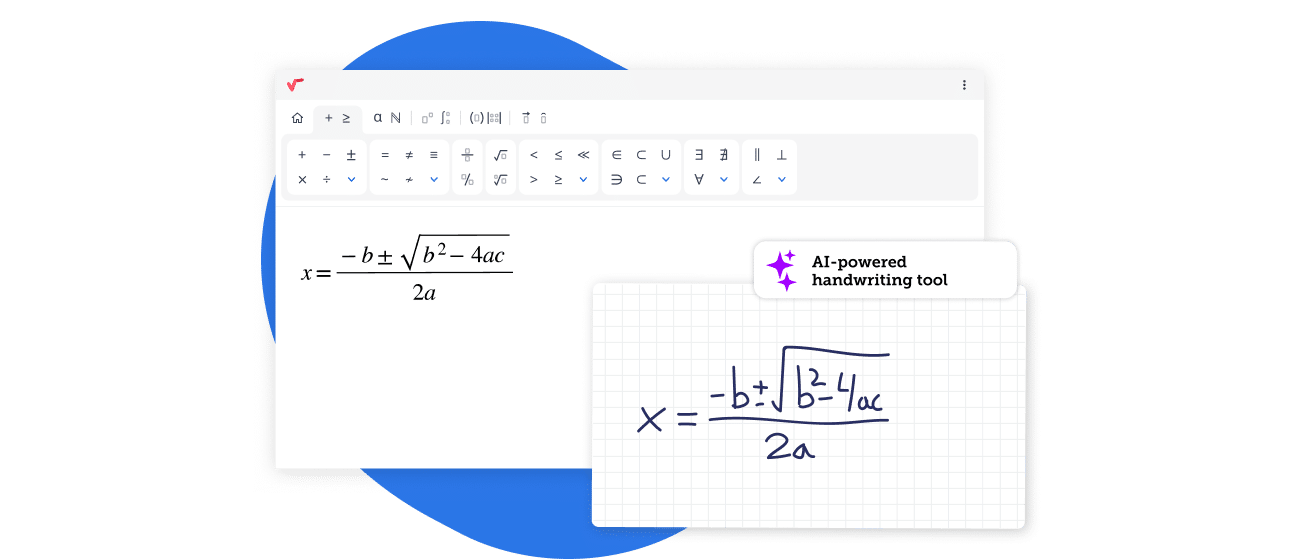
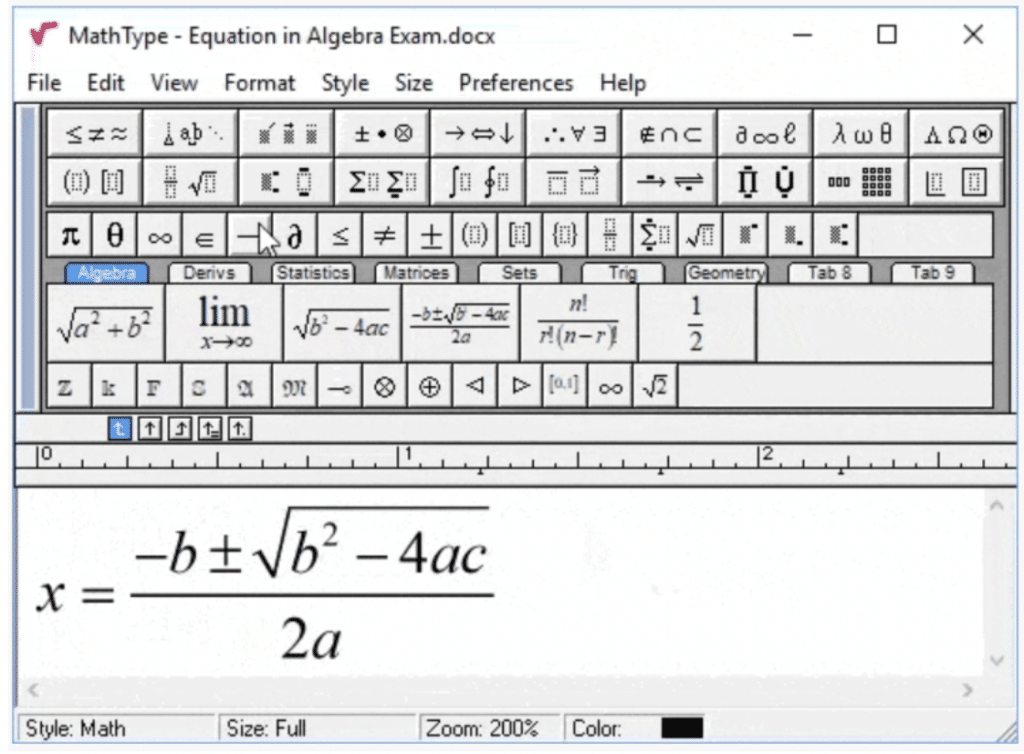
Moreover, creating math expressions at scale was complex. “Even embedding these equations as images was a challenge,” affirms Ryan. The team needed a tool that could streamline both authoring and reading math content, one that would make online math assessments seamless for teachers and students alike.

The MathType Fix: A Seamless Solution for ASSISTments

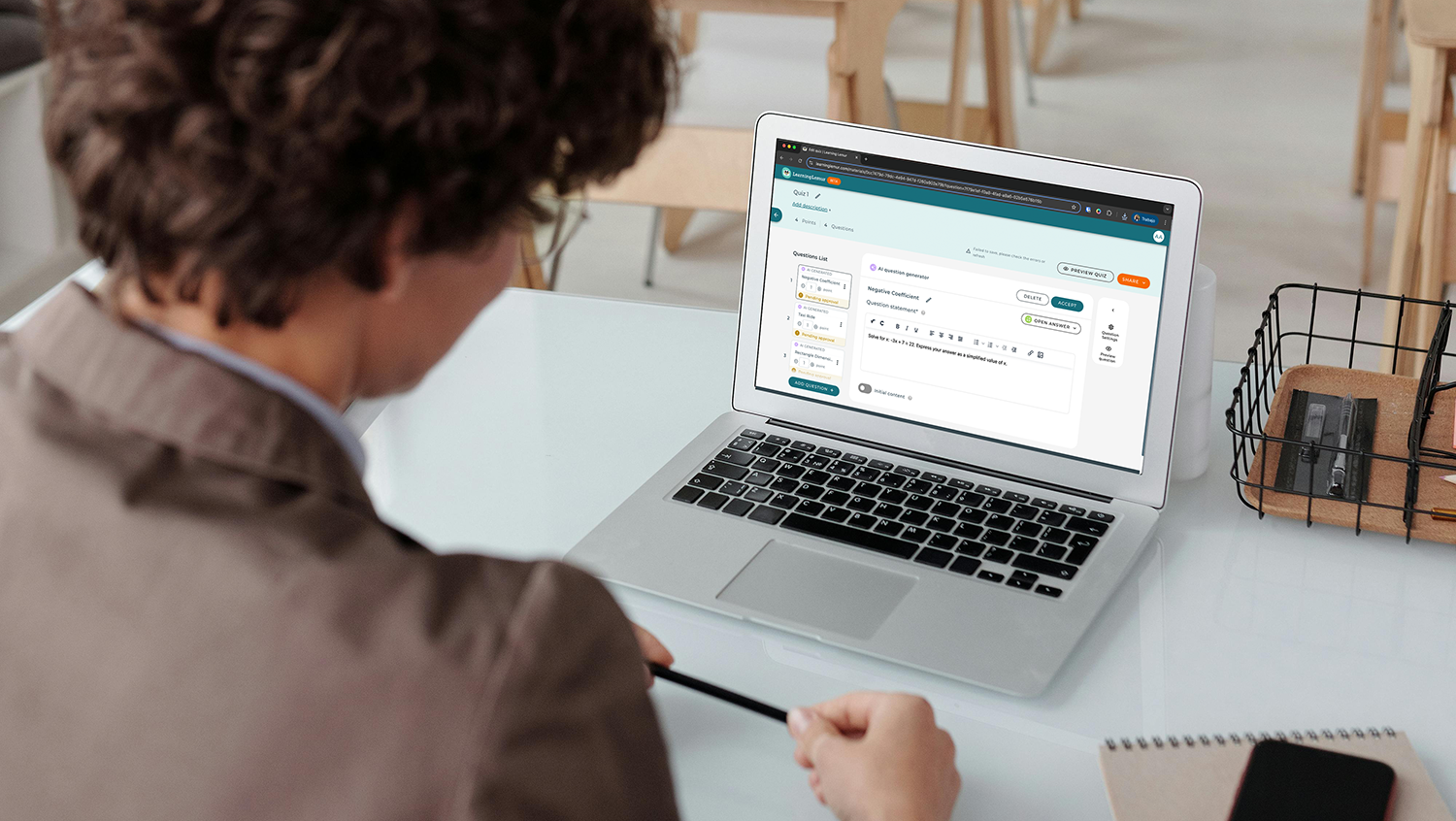
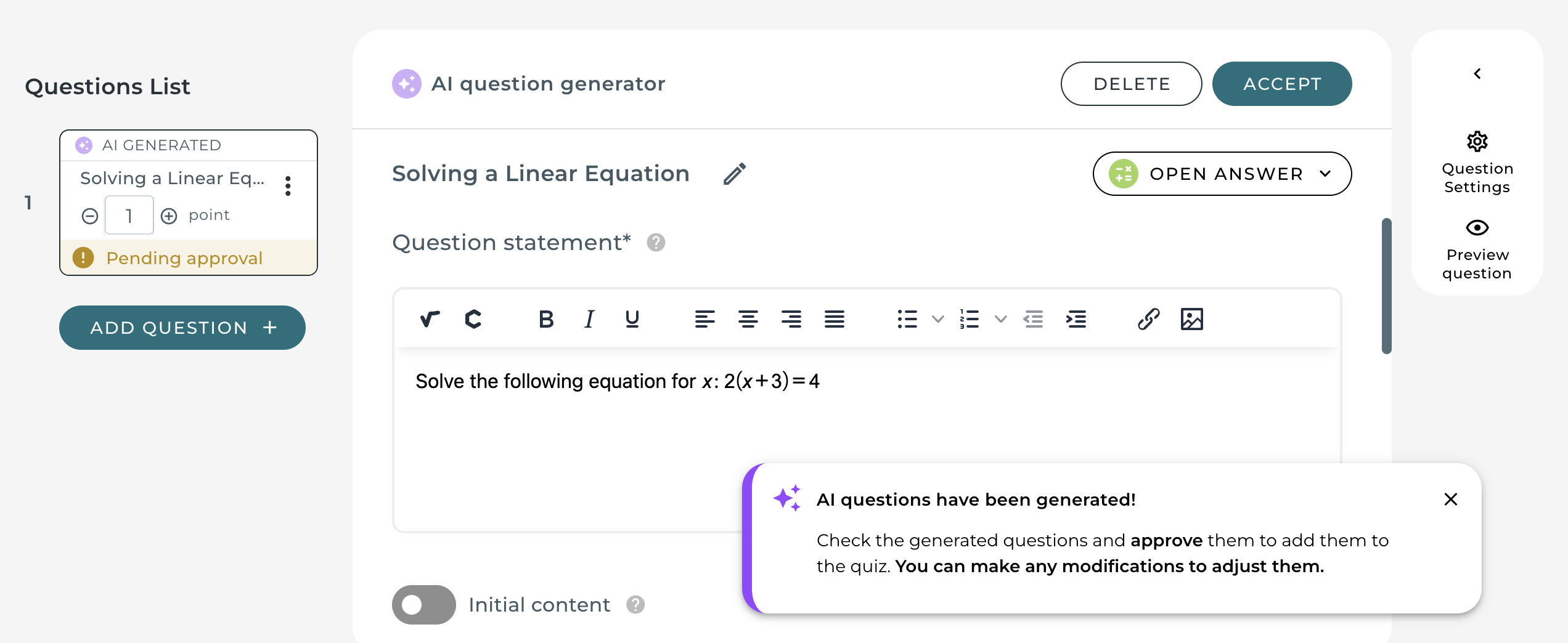
ASSISTments implemented MathType across their platform, embedding it in both question creation and student answer fields. This allowed math to be written, displayed, and interpreted consistently throughout the learning process. As Ryan explains, “We use MathType in both the questions and in student submissions.”

The impact was immediate. Teachers gained a reliable, familiar interface for authoring problems with clean math notation. Students could write expressions intuitively without memorizing syntax. And most importantly, the platform achieved standardization across its vast library of math problems.

Making Math Work at Scale: Implementation in Action

Scaling quality in math education takes more than good intentions: it requires the right tools, implemented thoughtfully. ASSISTments knew that achieving consistent, accessible math content across thousands of users meant getting the details right from the start.

Core Workflow: How Teachers and Students Use the Platform

ASSISTments began by identifying its core challenge: creating a math-friendly interface that supports content authors and enhances clarity for students. As Ryan explains, this need stemmed from the platform’s core functionality:

“Teachers assign work to their students […] and students complete their assigned work and get scores automatically.”

A flexible fit for diverse needs

Using MathType, the platform adapted to serve multiple user types. Whether authoring algebra questions or submitting open-ended answers, users interacted with the same consistent math input tool. This uniformity aligned perfectly with the curriculum’s needs.

Integration without headaches

Thanks to MathType’s flexible integration, the implementation was straightforward. Its seamless embedding allowed the engineering team to focus on building better content rather than managing formatting complexities.

results math assessment

What Changed: Results That Elevated Math Content Creation

When ASSISTments first integrated MathType, the decision wasn’t just about improving their platform: it was about choosing a partner that could grow alongside their vision. Over the years, they’ve never had to reconsider that choice. MathType has consistently met their evolving needs without requiring any major rework or integration changes.

This long-term reliability has become a cornerstone of their innovation strategy. As ASSISTments expanded their platform’s capabilities and scaled their offerings, MathType seamlessly supported these advancements. From classroom assessments to large-scale research implementations, MathType’s adaptability has proven indispensable.

Choosing MathType from the beginning meant having the right tool from day one, one that continues to support complex math authoring needs, no matter how far the platform evolves.

What’s Next: Scaling Innovation and Accessibility

Looking ahead, accessibility remains a key priority. “From an accessibility standpoint, we struggle with the use of images. […] It’s preferable if it could be rendered as text that was more directly read by the screen reader,” explains Ryan. The team is actively exploring how MathType could evolve to better support screen readers and align with accessibility best practices.

Beyond accessibility, ASSISTments is pushing boundaries in automation.

“We’re interested in pushing the bounds of what kinds of problems we can grade automatically: graphing problems, manipulatives… to ensure students still get immediate feedback and spare teachers the need to grade,” says Ryan.

MathType is expected to play a key role in scaling this vision.

Rounding Off: MathType’s Lasting Impact at ASSISTments

The collaboration between ASSISTments and MathType highlights the vital role of well-integrated math assessment tools in modern education. With MathType, ASSISTments has transformed its approach to math content creation, improving communication, accessibility, and scalability.

Ryan Emberling’s insights show that innovation in digital math content isn’t just about technology: it’s about designing tools that empower users at every level of the learning process.

Transform your platform with MathType now!

Uncategorized

Academic Dishonesty: Prevent It with Random Math Quizzes

Post author By Aida Alsina
Post date September 16, 2025

Online Learning Has a Cheating Problem, And It’s Growing

As education shifts rapidly to online and hybrid formats, academic dishonesty is becoming more prevalent and harder to detect. A comprehensive review in the scientific magazine Springer Nature Link of self-reported student behavior found that cheating in online exams rose from 29.9% before COVID to 54.7% during the pandemic.

A study published in the Online Learning Journal examined unproctored online exams in a large introductory biology course. Using LMS activity logs to detect whether students were navigating away from the test window, researchers found that up to 70 % of students did so, often on most questions. Appeals to student integrity or honor pledges had little effect, but a simple warning about potential detection combined with a penalty policy reduced this behavior to just 15 %. This study clearly demonstrates that the way an exam is designed—and students’ perception of oversight—has a much greater impact on academic honesty than the technology used itself.

These figures underscore a worrying trend: as reliance on screen-sharing, messaging apps, and generative AI increases, traditional anti-cheating measures struggle to keep pace. While most institutions promote academic honesty, digital environments introduce new vulnerabilities that traditional exams don’t account for. That’s where technology can help educators turn the tide.

The Risks of Academic Dishonesty in Online Assessments

Digital learning offers flexibility, but it also exposes gaps in control and assessment integrity. In particular, math quizzes and STEM evaluations are among the most affected. Why?

Students may copy solutions from peers in real time. During online exams or quizzes, students can easily communicate through messaging apps, video calls, or shared screens. In many cases, this allows them to collaborate during assessments that are meant to be individual. The lack of in-person supervision makes real-time copying far more difficult to detect than in a physical classroom.
Answer-sharing platforms often publish full collections of test questions and answers taken from real courses. This allows students to search for specific problems and find exact solutions, making it easier to cheat, especially in online assessments. These platforms pose a serious threat to academic integrity.
Automatic feedback loops allow repeated guessing until success. Many online quiz systems offer immediate feedback and unlimited attempts without any variation in the questions. While useful for formative learning, this can be exploited during summative assessments, as students may guess repeatedly or try out answers until they find the correct one, rather than understanding the underlying concepts.
Identity verification is difficult in unsupervised settings. Without secure login procedures or proctoring tools, it becomes difficult to ensure that the student completing an online exam is actually the one enrolled in the course. This opens the door to impersonation, paid test-taking services, and other forms of academic fraud that are difficult to trace after the fact.

Randomized Math Quizzes: A Smart Strategy for Academic Honesty

To protect the integrity of online math assessments, many institutions are turning to randomized math quizzes. These assessments use variable-driven content to generate unique versions of the same problem for each learner.

Why Randomization Works

Randomization is effective because it ensures that each student receives a unique version of the same problem. By generating different sets of variables, it becomes nearly impossible for learners to share answers or copy from one another. This approach maintains the same logical structure and learning objectives for all, but with varying inputs that require independent resolution. It also enables educators to automatically regenerate problems, scaling assessments without compromising integrity. Ultimately, randomized math quizzes mirror real-world problem-solving environments, where conditions change and memorization alone is insufficient, encouraging students to apply concepts rather than recall patterns. Randomized quizzes not only deter academic dishonesty: they also promote deeper learning by encouraging individual problem-solving strategies.

Insert random variables into a math question using WirisQuizzes.

How WirisQuizzes Prevents Academic Dishonesty

WirisQuizzes is Wiris’ robust assessment solution designed specifically for STEM education. It enables educators to create rich, dynamic math questions adapted to each student’s context. By introducing random variables, the platform generates virtually unlimited versions of the same problem, discouraging cheating and promoting deeper engagement. Its intelligent grading engine automates correction and delivers immediate feedback, encouraging learning through exploration and repetition.

WirisQuizzes offers built-in random variable generation designed specifically for math and STEM contexts. Unlike generic quiz platforms, WirisQuizzes understands the structure of math and allows educators to define flexible, yet pedagogically consistent, question templates.

With WirisQuizzes, educators can:

Define variable ranges for values like x, a, b, or θ
Create multiple conditions to ensure solvable and meaningful outputs
Randomize both numerical and algebraic parameters
Use automatic validation logic to verify correct answers per version
Preview multiple quiz versions before deploying

This dynamic approach allows hundreds of quiz variations to be generated from a single question model, keeping assessments fair, secure, and scalable.

Real-World Applications: From Schools to Universities

The effectiveness of randomized math quizzes powered by WirisQuizzes has been demonstrated across various educational levels:

Secondary Education

In middle and high schools, teachers use WirisQuizzes to generate personalized homework assignments and quizzes tailored to each student. Even though the problems test the same concepts, every learner receives a unique version with different variables. This significantly reduces opportunities for copying among classmates, while still aligning with the curriculum. As a result, students engage more deeply with the material and take greater ownership of their learning process.

Higher Education

In colleges and universities, professors rely on WirisQuizzes to deliver fair and secure assessments for large cohorts without manually creating dozens or hundreds of different exam versions. By using random variables to generate unique yet equivalent problems, educators can maintain academic integrity even in high-stakes midterms and finals. This is especially valuable in large-enrollment STEM courses like calculus, linear algebra, and statistics.

Online Learning Platforms

EdTech platforms and online learning providers integrate WirisQuizzes into their learning management systems (LMS) to offer secure, scalable assessments to a broad user base. Randomized question generation ensures each learner faces a unique challenge, making answer sharing or mass cheating far more difficult. Combined with immediate feedback and intelligent grading, this approach supports adaptive learning and high levels of academic integrity across thousands of users.

More Than Prevention: Promoting Academic Honesty by Design

Preventing academic dishonesty is only one side of the equation. Tools like WirisQuizzes also encourage academic honesty by fostering independent thinking and personalized learning.

When students know that each problem is unique to them, they are more likely to engage with the material rather than memorize solutions, develop critical thinking and conceptual understanding, and trust that their efforts are being fairly evaluated. This shift in mindset contributes to a culture of integrity.

Make Cheating Obsolete With Randomization

In an era where cheating can happen with a few clicks, prevention must be proactive, not punitive. Randomized math quizzes provide a smart, scalable way to ensure fair assessments and promote academic honesty.

WirisQuizzes empowers educators to build dynamic, variable-driven math assessments that are both secure and student-centered.

Prevent academic dishonesty with WirisQuizzes

Uncategorized

Hybrid Learning in Math Education: Why Blending Online and Offline Instruction Matters

Post author By Aida Alsina
Post date September 9, 2025

Hybrid learning, also known as blended learning, is an educational approach that combines traditional face-to-face instruction with digital, online components. Instead of treating online and offline learning as separate modes, hybrid learning integrates both in a coordinated and intentional way. The goal is not simply to alternate between classroom and remote activities, but to design a cohesive experience that leverages the strengths of each environment—flexibility, accessibility, interaction, and personal connection. This model has gained significant traction in recent years, especially in math education, where abstract concepts and diverse learning needs benefit from varied modes of engagement.

Hybrid learning is reshaping how we teach and learn math. By blending digital tools with in-person instruction, educators can offer more personalized, effective, and engaging learning experiences.

This approach doesn’t replace traditional methods: it enhances them. It respects the emotional and cognitive aspects of learning and responds to the reality of modern classrooms, where students have diverse learning paces, styles, and circumstances.

Blended learning is not a trend but a pedagogical shift that bridges accessibility, adaptability, and human connection.

The Power of Combining Online and Offline Math Instruction

Blended learning in math education creates a synergy that neither modality can achieve alone. As math educators adapt to evolving student needs and technological possibilities, this combined model offers:

Flexibility: Students can access digital resources anytime, which is particularly helpful for review or reinforcement outside the classroom.
Interactivity: Online tools bring math concepts to life through animations, simulations, and interactive problem-solving platforms.
Human Connection: Face-to-face instruction fosters real-time discussion, emotional support, and immediate feedback.
Scalability: Educators can manage large or diverse groups more efficiently, offering tailored support where needed.

In math, where abstract concepts often require iterative exploration, hybrid learning empowers both guided instruction and independent thinking. It accommodates repetition, variation, and collaborative exchange, all crucial for deep understanding. By combining the immediacy of in-person learning with the accessibility of online math teaching, educators can truly transform their practice.

Balance Between Structure and Autonomy in Hybrid Learning

One of the central strengths of hybrid learning is its ability to balance learning framework and autonomy. Math learning demands both: structured pathways to introduce and build skills progressively, and autonomy to foster individual exploration, confidence, and critical thinking. Blended learning strategies provide the framework for this balance, supporting both consistency and creativity in math classrooms.

Online: Providing Structure and Individual Pacing

Online environments offer a structured framework for learning. Through curated modules, step-by-step explanations, and automated feedback, students gain clarity and consistency. The self-paced nature of online platforms allows students to revisit concepts, practice at their own rhythm, and receive immediate guidance, which is especially valuable for mastering foundational skills.

Tools like WirisQuizzes, a platform designed specifically for math and STEM assessments, enhance this experience by offering dynamic, auto-corrected questions with random variables. This not only provides individualized practice opportunities but also ensures that students engage actively with the material rather than passively memorizing answers. Online math teaching empowers learners by offering them control over their pace and focus areas, reinforcing competence and motivation.

Offline: Promoting Dialogue and Deeper Reasoning

Offline, classroom-based instruction adds the relational and spontaneous aspects of learning. In-person sessions encourage students to articulate their reasoning, ask questions, and collaborate on complex problems. Teachers can detect misunderstandings in real time and adapt explanations. These interactions develop mathematical communication skills and help students connect theory with practice. This live component of hybrid learning ensures that math remains a social, responsive, and human-centered discipline.

Together, these modalities reinforce each other. Structure without autonomy may feel rigid; autonomy without structure may lack direction. Hybrid learning aligns both.

Visual and Symbolic Thinking

Math is both visual and symbolic. Hybrid learning supports this duality by using digital tools to represent abstract ideas and classroom environments to interpret and discuss them.

Online platforms like WirisQuizzes or Learning Lemur (our intuitive math platform integrated with Google Classroom that provides customizable quizzes, automatic grading, and personalized feedback) can visualize functions, geometric transformations, or algebraic manipulations interactively. These representations complement traditional symbolic work and help learners form mental models. In-person settings then provide the space to reflect on and interpret these representations with peers and educators, solidifying understanding.

school learning

By moving fluidly between visualizations online and symbolic manipulation offline (and vice versa), students strengthen their conceptual grasp. This kind of dynamic interplay is a key benefit of hybrid learning, enabling learners to connect different forms of mathematical representation more effectively.

Real-World Applications of Hybrid Learning in Math

Hybrid learning is not just a theoretical framework, it is being put into practice across a wide variety of educational settings. From urban schools to rural learning centers, educators are designing innovative ways to integrate digital and face-to-face instruction in their math classrooms. These practical applications demonstrate how blended learning strategies can meet diverse educational needs while maintaining quality and engagement.

Among the many institutions that already apply the hybrid learning system, we can find 21K School (United Kingdom), Harvard University (USA), Massachusetts Institute of Technology (USA), and public schools in Singapur.

Use Cases from Classrooms Worldwide

A high school teacher flips the classroom: students watch instructional videos and complete guided exercises at home, while class time is used for collaborative problem-solving.
A university professor alternates between digital assessments and in-person workshops, combining online scalability with live, hands-on support.
A community center in a low-connectivity area uses downloaded interactive materials during the week and organizes weekend math clubs with volunteer educators.

These real-world models show how hybrid learning can be tailored to different contexts, always seeking to optimize both access and engagement.

A Human-Centered Vision of Technology: The Wiris Approach

Wiris strives to maintain a modern and technological outlook without losing sight of the human and natural essence of education and scientific inquiry. In Wiris, we believe that true innovation does not come at the expense of personal connection, but it builds upon it. This philosophy aligns perfectly with the hybrid learning model, which combines the strengths of digital tools with the irreplaceable value of in-person instruction.

Wiris designs tools that reflect this vision. These tools are not about replacing educators or standardizing learning. They aim to empower teachers and students within the hybrid model that embraces this balance of structure and autonomy, visual and symbolic reasoning, digital reach, and human connection.

WirisQuizzes, for example, supports hybrid education with customizable, automatically graded math quizzes powered by random variables—ensuring individualized learning while maintaining academic rigor.

MathType complements this approach by providing an intuitive editor for writing mathematical notation across multiple platforms, enabling seamless symbolic communication in both digital and physical learning environments.

LearningLemur, our intuitive math platform designed specifically for Google Classroom, offers interactive, customizable quizzes with automatic grading and personalized feedback. It transforms how students engage with math exercises, providing visual support and adaptable content that fits any hybrid learning strategy.

Embracing the Future of Math Instruction

As the line between digital and physical classrooms continues to blur, embracing hybrid learning isn’t just an option: it’s a necessity. With the right methodology and the right tools, we can build a future of math instruction that is inclusive, adaptive, and deeply connected to the needs of students and educators alike.

Explore how Wiris supports hybrid learning here

Uncategorized

Math Content Creation: How Cambridge HOTmaths Improved Math Publishing

Post author By Aida Alsina
Post date August 26, 2025

Empowering Math Education with the Right Tools

Creating math-rich content for digital and print formats is no small feat, especially when your audience includes thousands of educators and students across Australia and New Zealand. For Cambridge HOTmaths, producing visually accurate and accessible math content was a major challenge. That changed with MathType, a powerful equation editor by Wiris that allows users to create and edit mathematical notation across digital and print platforms. It integrates seamlessly with tools like Microsoft Word and supports LaTeX, making it ideal for educators and content creators.

In this success story, you’ll learn how MathType revolutionized content creation at Cambridge HOTmaths, giving their editors full control and efficiency while enhancing accessibility and output quality.

Meeting the Challenge in Digital Math Publishing

Before using MathType, the process at Cambridge HOTmaths involved:

Inserting individual images for each math fraction or expression
Relying on graphic designers for any edits
Managing inconsistent formatting and accessibility issues

“We previously used images for calculations and fractions, which had to be sent to the graphic artist for any amendments or corrections,” explains Penny Redfearn, Content Manager at Cambridge HOTmaths.

Transition to Better Math Content Creation

The adoption of MathType marked a turning point. With MathType, the content team gained full control over equation editing directly within Microsoft Word. Editors no longer had to manually insert and align each fraction image: they could type everything as if it were regular text. “The editors no longer need to insert each fraction individually as an image and centre it. We have full control of creating maths content involving calculations”, affirms Penny.

Additionally, the transition to LaTeX-based output with MathType significantly improved web accessibility. “Replacing images with LaTeX improved our website accessibility significantly.”

hotmath mathtype

How MathType Fits Into Their Workflow

Cambridge HOTmaths uses MathType in two primary ways:

Microsoft Word Worksheets: MathType is used to insert all math expressions directly into documents, which are then exported to PDF for distribution.
Website Equations: MathType helps generate LaTeX that can be adjusted and integrated into their platform’s custom LaTeX math editor.

While some final LaTeX tweaks are still made manually, MathType provides an efficient starting point. “We often use MathType to give us a LaTeX template and then we can fit with it”, says Penny. MathType has become an essential LaTeX math editor for the team, streamlining both print and web-based equation creation.

The Right Education Math Tools for the Right Roles

Only a small team at Cambridge HOTmaths is responsible for content creation, making usability and reliability essential. MathType’s consistency, style settings, and shortcut support proved invaluable. “We’ve got styles set up so that everything’s consistent every time we create a new equation in the document.” Among the many education math tools available, MathType stood out for its balance of functionality, consistency, and ease of use.

The team relies on shortcut keys (e.g., Ctrl+H for superscript, Ctrl+L for subscript), making equation writing quick and intuitive. “I’ve been using MathType ever since it was created… it’s been great.”

Redefining Math Content Creation in Education

For Cambridge HOTmaths, MathType is more than a math editor. It’s a productivity booster, accessibility enhancer, and creative enabler. Its integration into their publishing workflow has helped streamline content creation, reduce reliance on graphic designers, and ensure consistent math presentation across print and web formats.

With their sights set on expanding interactivity and user engagement, MathType and the wider Wiris ecosystem are well-positioned to support Cambridge HOTmaths as they continue leading math education innovation.

Want to explore how MathType or WirisQuizzes can support your institution’s math content creation and assessment needs?

Discover MathType

Uncategorized

From Education to Engineering: Why Efficient Math Writing Matters

Post author By Aida Alsina
Post date August 18, 2025

In today’s data-driven world, math content has become a core asset for innovation, communication, and decision-making. Whether you’re designing algorithms, explaining a financial model, or building educational materials, math writing plays a key role in turning complex ideas into actionable insights.

Creating accurate, clear, and accessible math content is no longer a task limited to academia: it is a necessity for sectors that rely on precision and knowledge transfer.

Where Math Content Creation Matters Most

Numerous industries and knowledge domains depend on the ability to produce, adapt, and distribute high-quality math content:

Education and EdTech

In the educational ecosystem, math content creation is foundational to the learning experience. Teachers, curriculum designers, edtech developers, and instructional designers rely heavily on precise math writing to prepare lesson plans, assessments, and interactive digital resources. From primary education to advanced university-level courses, the clarity of mathematical expressions can directly impact student comprehension and performance.

Moreover, in EdTech platforms, the challenge is not only pedagogical but also technological: math equations must be compatible with multiple devices, formats, and learning management systems (LMS). An efficient math editor empowers educators to quickly create, edit, and share content that maintains its structure and meaning across platforms. In this context, robust math content creation tools are essential to promote equity, consistency, and accessibility in modern education.

mathtype editor — *Example of math formula written with Wiris’ MathType*

Scientific Communication and Research

Research in fields like physics, chemistry, biology, and mathematics relies on formalized, structured math writing to present hypotheses, validate results, and communicate findings. From peer-reviewed journals to preprints and grant applications, the presentation of math content can influence not only understanding but also the perceived credibility and professionalism of the work.

In scientific communication, reproducibility is key, and that begins with clear, accurate notation. A powerful math editor allows researchers to format complex expressions with ease, whether writing in LaTeX or using WYSIWYG interfaces. Additionally, the ability to produce accessible and well-structured math content supports broader dissemination and interdisciplinary collaboration, enabling scientists to reach audiences beyond their immediate field.

Engineering and Technical Fields

Engineers and technical professionals deal with complex models, formulas and simulations daily. Whether it’s civil, mechanical, electrical or software engineering, math writing is central to documenting calculations, designing systems and validating outcomes. A minor error in notation can lead to misunderstandings or costly consequences in design and implementation.

Creating high-quality math content in this context requires precision, standardization, and compatibility with technical documentation tools. An advanced math editor enables teams to present formulas clearly, integrate them into CAD documentation or specifications, and ensure that the mathematical logic behind a project is both transparent and reproducible. In collaborative engineering environments, clarity in math content helps avoid ambiguity and streamlines review and approval processes.

Economics and Finance

In economics and financial analysis, mathematics is the language of logic and prediction. Economists, analysts, and consultants must build models, define formulas, and perform complex calculations that underpin reports, forecasts, and strategic decisions. The credibility of these outputs often depends not just on the numbers but on how clearly the underlying methodology is communicated.

Effective math writing is crucial to ensure that stakeholders -be they clients, regulators, or internal teams- understand and trust the content being presented. A professional math editor facilitates the creation of visually coherent, publication-ready equations that can be embedded in reports, dashboards or academic publications. By investing in better math content practices, financial institutions and think tanks can enhance transparency and drive data-informed decisions.

Corporate Innovation and Data Teams

In corporate environments, especially within innovation, R&D, and data science teams, math content is integral to documenting algorithms, models, and analytical frameworks. These teams often work cross-functionally with product managers, developers, and decision-makers, making it essential to express complex logic in a format that is both technically correct and easily interpretable.

Whether it’s machine learning formulas, operational models, or optimization strategies, professional math writing improves internal communication and project documentation. A reliable math editor can help standardize the way mathematical reasoning is presented across teams and documents, accelerating onboarding, compliance, and strategic planning. As companies increasingly rely on data-driven methodologies, structured math content becomes a competitive advantage.

The Value of Clear and Consistent Math Writing

High-quality math writing opens the door to significant strategic advantages for any organization. When math content is clear, accessible, and professionally formatted:

Technical data is interpreted correctly, enabling informed decision-making across teams and stakeholders.
Research and analysis are communicated clearly, enhancing dissemination, credibility, and engagement with diverse audiences.
Efficiency improves, as well-formatted math content reduces the need for time-consuming corrections and rework.
Cross-functional collaboration becomes easier since standardized content facilitates understanding between departments, institutions, or international partners.

By prioritizing structured and coherent math content, organizations position themselves for success in education, research, development, and beyond.

MathType: A Math Editor Designed for Today’s Needs

Once we acknowledge the strategic value of math content, the next step is choosing the right tool to support it. MathType is the world’s leading equation editor that allows you to write math notation as easily as you write text. Trusted by educators, researchers and professionals across the globe, it is used by K-12 and university STEM students and faculty worldwide.

Here’s why:

Seamless math writing experience.
MathType enables professionals to write equations as intuitively as regular text. Whether using a keyboard, mouse, or stylus, it adapts to your workflow.

500+ mathematical symbols and structures
MathType offers an extensive symbol library covering arithmetic, algebra, calculus, logic, and more. This allows users to express even the most complex mathematical concepts accurately, avoiding improvisations or workarounds that compromise clarity.
AI-powered handwriting recognition
Users can handwrite equations using a stylus or touch interface, and MathType will instantly convert them into digital math expressions. This accelerates math writing and bridges the gap between traditional note-taking and digital editing.
Export in high-quality formats: SVG, PNG, PDF
MathType generates visually clean equations that can be exported in multiple file formats. Whether for web, print, or presentation use, the quality remains intact, making your math content consistent across platforms.
Accessibility-compliant outputs
The editor ensures all math expressions meet accessibility standards, supporting screen readers and enabling inclusive communication. This is crucial for educational institutions and public sector projects with accessibility requirements.
Integration and customization
MathType integrates with LMS, CMS, HTML/XML editors, and supports customizable formats, making it ideal for scalable projects and diverse user needs.
Support for LaTeX and MathML
Ensure compatibility with standard math markup languages used in academic, technical, and publishing environments.
Includes ChemType for chemistry notation
Edit and format chemical equations with a dedicated toolbar for editing inorganic chemistry notation, supporting scientific professionals with highly specific formatting needs.

editor chemtype — *Example of chemical formula written with Wiris’ MathType*

Invest in Smarter Math Content Creation

In a world where precision, clarity, and accessibility are essential, organizations can no longer treat math writing as an afterthought. Whether you’re educating future scientists, validating engineering designs, or presenting complex financial models, the quality of your math content directly impacts how your message is understood, trusted, and acted upon.

Adopting a professional-grade math editor is not just a matter of convenience: it’s a strategic decision that supports consistency, collaboration, and efficiency across the organization.

Catch up on efficient math equations with MathType

Uncategorized

Understanding the Power of e number: The Unsung Hero of Mathematics

Post author By Aida Alsina
Post date August 5, 2025

When discussing fundamental mathematical constants, pi often takes the spotlight. However, another number, equally vital yet less celebrated, is Euler’s number e. Known simply as e, this constant appears in countless mathematical contexts and real-world applications. In this article, we will explore the origin, properties, and applications of e, positioning it as an indispensable tool in the worlds of mathematics, science, and finance.

What Is Euler’s Number e?

Euler’s number e is an irrational and transcendental number, approximately equal to 2.71828. It serves as the base of natural logarithms and arises naturally in various growth processes and limit calculations.

The Origin of e: A Practical Example

Consider the following real-life scenario: Imagine a bank offering a 100% annual interest rate on a principal investment of 1€. If interest is compounded once at the end of the year, you would have 2€. However, if the bank compounds interest semiannually at 50% every six months, the calculation changes:

After six months: 1€ × 1.5 = 1.5€
After another six months: 1.5€ × 1.5 = 2.25€

Now, let’s divide the year into three periods of four months each, applying an interest rate of 33.33% every four months:

After four months: 1€ × 1.33 = 1.3333€
After eight months: 1.3333€ × 1.3333 ≈ 1.7777€
After twelve months: 1.7777€ × 1.3333 ≈ 2.3703€

So, if you receive infinite payments, will you have infinite money? Unfortunately, the answer is no. As the frequency increases -from quarterly to monthly, to daily, and beyond- the final amount approaches a limit. The formula to calculate this is:

mathtype formula Image created with Wiris’ MathType

As n approaches infinity, the value converges to e. This simple yet powerful example demonstrates the natural emergence of e in exponential growth, explaining its foundational role in continuous compounding interest models.

Fundamental Properties of e Number

Irrationality: e cannot be expressed as a simple fraction.
Transcendence: e is not a root of any non-zero polynomial equation with rational coefficients.
Infinite Series: e can be represented as the sum of the infinite series:

equation with mathtype

Image created with Wiris’ MathType

Natural Logarithm Base: The function uses e as its base, integral to calculus and natural growth models.
Euler’s Identity: Considered one of the most beautiful equations in mathematics:

eⁱ^π+ 1 = 0

This equation elegantly connects five fundamental mathematical constants: 0, 1, e, i, and π.

Applications Across Disciplines

Euler’s number e is not only a fundamental constant in pure mathematics but also plays a pivotal role in a range of practical applications across various scientific and technological fields. From modeling growth processes to risk management, e is indispensable in understanding and predicting complex phenomena.

In Mathematics

Calculus: Euler’s number is central to calculus, particularly in the context of exponential growth and decay. One of the most important properties of e is that the derivative of the function e^x is e^x itself. This unique property makes it extremely useful in solving differential equations that describe dynamic systems, such as population growth, radioactive decay, and heat transfer. It simplifies the analysis of these systems because the function is self-replicating under differentiation.
Complex numbers: Euler’s formula, e^ix = cos(x) + isin(x), is one of the most profound equations in mathematics, linking exponential functions with trigonometric functions. This relationship is crucial in fields like electrical engineering and signal processing, where it simplifies the analysis of oscillating systems and waveforms. It allows for a more intuitive understanding of rotations and oscillations in the complex plane.

In Physics

Radioactive decay: The process of radioactive decay follows an exponential law, which can be modeled using e. The amount of a radioactive substance remaining after a certain period is given by the equation N(t) = N₀e^λt, where N(t) is the amount of substance at time t, N(t) is the initial amount, and λ is the decay constant. This model is used to predict the behavior of radioactive materials over time, which has applications in medicine (e.g., radiology), archaeology (e.g., carbon dating), and nuclear physics.
Thermodynamics: In thermodynamics, the Boltzmann factor (see image below) is essential for determining the probability of a system being in a particular energy state, where 𝐸 is the energy, 𝑘 is the Boltzmann constant, and 𝑇 is the temperature. This exponential relationship is vital in understanding systems in equilibrium, such as the distribution of particles in gases or the behavior of molecules in biological processes.

In Economics and Finance

Continuous compounding: One of the most common uses of e is in the calculation of continuously compounded interest. If interest is compounded continuously rather than at discrete intervals, the formula for the accumulated value of an investment becomes A = Pe^rt, where 𝑃 is the initial investment, 𝑟 is the interest rate, and 𝑡 is the time in years. This formula highlights how the frequency of compounding approaches a limit, with e representing the limit as compounding becomes continuous. It is fundamental in understanding the long-term growth of investments and savings.
Risk models: Financial models such as the Black-Scholes model for option pricing rely heavily on e to account for the stochastic nature of asset prices. The formula for option pricing involves exponential functions to model how the price of an option evolves over time. e also plays a key role in various risk models, including Value at Risk (VaR) calculations, where it helps quantify the likelihood of extreme losses in investment portfolios.

In Technology

Algorithms: Euler’s number is used in algorithmic analysis, particularly when analyzing the performance of algorithms that exhibit exponential growth. For instance, certain random processes and algorithms, such as the analysis of QuickSort (a widely used sorting algorithm), can involve e. Specifically, in probabilistic algorithms and complexity theory, e appears in the expected running time of algorithms, as they often follow exponential distributions or involve recursive calculations that converge to e.
Machine learning and data science: In machine learning, e is frequently involved in algorithms that model growth processes or in optimization algorithms that use exponential decay to adjust parameters over time. For instance, in gradient descent, which is used to find the minimum of a function, learning rates may decay exponentially based on e to optimize performance and prevent overshooting.

In Biology and Medicine

Population growth: One of the most well-known real-world applications of e is in modeling population growth. When populations grow in ideal conditions (without external limitations), the number of individuals follows an exponential growth curve, which is modeled by the equation, P(t) = P₀e^rtwhere 𝑃(𝑡) is the population at time 𝑡, P₀ is the initial population, and 𝑟 is the growth rate. This principle is not only relevant to ecology but also helps in understanding the spread of diseases in epidemiology.
Pharmacokinetics: The exponential decay model is also used in pharmacokinetics, which studies how drugs are absorbed, distributed, metabolized, and excreted by the body. The concentration of a drug in the bloodstream over time often follows an exponential decay, and the parameter governing the decay is related to e. This helps in determining dosing schedules for medications to ensure therapeutic levels are maintained without causing toxicity.

Visualizing Euler’s Number e with Wiris’ Digital Tools

As digital solutions advance, tools like MathType and CalcMe empower users to work effortlessly with e and other complex mathematical expressions. Whether you’re a researcher, educator, or professional, integrating these Wiris’ technologies into your workflow ensures precision and efficiency.

For instance, to deepen the understanding of e’s behavior, one can visualize the limit expression

equation editor

using graphing tools such as CalcMe, a Computer Assisted System (CAS) for algebraic manipulation that allows complex mathematical calculations to be carried over in a self-contained, fast and intuitive way. As increases, the graph approaches the value of number e, offering an intuitive graphical demonstration of this mathematical limit.

Additionally, MathType, the world’s leading equation editor that allows you to write math notation as easily as you write text, enables seamless insertion of complex mathematical expressions into documents and web content, ensuring clarity and precision.

number e graphic

Graph showing the function (1+1/x)^x in red, approaching the value of e in blue.

Perfect for students, teachers, editors, and technical writers, MathType streamlines the creation of high-quality technical and scientific content across various platforms.

For seamless handling of mathematical expressions and visualizations, consider incorporating both MathType and CalcMe into your digital toolkit.

Write your e number equations here!

Uncategorized

Irreplaceable Formulas: MathType and Mondadori Education’s Editorial Excellence

Post author By Aida Alsina
Post date July 28, 2025

From a Useful Tool to a Strategic Company Reference

When Pietro Curci joined Le Monnier (an Italian publishing house) in the mid-1990s, he was already on the lookout for ways to modernize the production of educational content in his company, especially the most complex part: math formula typesetting. As head of the graphic office, his responsibility was clear: ensure quality, consistency, and efficiency in a publishing environment.

It was during those years, well before Le Monnier was acquired by the Mondadori Education Group (the biggest publishing company in Italy) in 1999, that Curci discovered MathType for Word. The equation editor quickly became indispensable, offering a way to produce clean, editable, and reusable formulas, something that was unheard of at the time. The Mondadori Education Group operates in three main areas: books (publishes fiction, non-fiction, children’s, educational, and academic books); magazines (publishes leading Italian print and digital magazines), and retail (manages a large network of bookstores and online sales). It is also active in education, digital content, and international licensing.

When the transition to Mondadori Education happened, so did the natural evolution of MathType from a useful tool to a strategic standard. Today, as Head of the Graphic Office for the Humanities Area for high schools, Curci oversees a large part of the group’s editorial workflow, and MathType remains at its core. Nearly three decades later, it remains a cornerstone of Mondadori Education’s editorial workflow. “Our solution is used by DeaScuola and Rizzoli Education, which are part of the Mondadori Education Group”, explains Curci.

What started as a practical solution for writing equations in Word has grown into something much bigger. Over time, MathType has become deeply embedded in how Mondadori Education works.

It’s not just used by one team or for one task, but it supports different departments and adapts to various parts of the production process. Whether in editorial or digital, MathType has proven to be flexible and reliable, earning its place as a shared reference point across the company.

The Challenges

In the mid-1990s, Le Monnier -and later Mondadori Education- needed a reliable tool for producing complex mathematical content. Curci recalls the limitations of early typesetting systems, particularly when it came to consistency, reusability, and integration with publishing tools like QuarkXPress.

“We needed something stable that would allow us to reuse content across editions and titles,” Curci explains. “MathType gave us formulas as images, and an image, as I always say, is forever. It was revolutionary“.

But over time, challenges evolved. The rise of digital publishing, colored content, and interactive formats pushed editorial tools beyond what black-and-white workflows could support. Ensuring compatibility with new operating systems and modern layout tools became a strategic necessity.

Mondadori Education and Wiris: Joint Efforts to Improve the Product

Mondadori Education adopted MathType in its early versions and never looked back. The company standardized its use across internal and external collaborators. Layout professionals, editors, and authors could all work with the same equation editor, streamlining collaboration.

“With the plugin installed in our platforms, we can extract formulas without redigitizing them. It saves time and reduces errors, something essential when you’re dealing with 5,000+ formulas in a textbook”, affirms Curci.

When Curci and his team encountered barriers -such as color rendering issues, EPS compatibility, or font glyph problems- they didn’t give up with MathType. Instead, they worked closely with Wiris, contributing practical solutions and insights based on their real-world workflow.

MathType’s flexibility in exporting MathML for digital editions, while maintaining high-quality image-based formulas for print, allowed Mondadori Education to meet evolving demands without rebuilding their content library from scratch. As Curci affirms, “Thanks to the embedded MathML, we can easily export the formulas as code and reuse them in digital formats”.

The Implementation Process

The implementation of MathType at Mondadori Education was the result of a clear vision: to establish a unified, efficient workflow for mathematical content creation. Once MathType proved to be a reliable solution, it was adopted as the official standard across the organization. This meant that all external vendors producing math formula typesetting layouts were also required to work with the same tool, fostering consistency and compatibility across every stage of production.

One of the key advantages of MathType was its ability to generate formulas as images, allowing for the long-term reuse of content. Thanks to this, legacy materials could be updated by simply adjusting style preferences, eliminating the need to recreate thousands of formulas from scratch.

The integration of MathType enabled seamless collaboration. Editorial teams received manuscripts with embedded formulas and passed them on to layout professionals, who could extract and edit the formulas directly, greatly reducing manual intervention and improving version control.

Throughout this process, Pietro Curci played a crucial role in bridging the gap between user needs and technical development. His collaboration with Wiris led to the resolution of various challenges, such as color rendering issues in EPS files, overprint settings in InDesign, and glyph compatibility. These contributions helped shape subsequent versions of the equation editor and ensured its alignment with real-world editorial demands.

Why MathType Is Essential to Mondadori Education’s Editorial Excellence

Over the years, MathType has established itself as a trusted and indispensable tool within Mondadori Education’s editorial ecosystem. Its ease of use, compatibility across platforms, and ability to generate both print and digital outputs have made it a core component of the company’s workflow. The following key benefits highlight why MathType continues to play a strategic role in ensuring quality, efficiency, and long-term content reuse at Mondadori Education.

Preserved editorial legacy. “MathType is irreplaceable,” says Curci. “Without it, we would have lost a huge amount of content or had to reinvest in recreating everything”.
Increased efficiency. Automated extraction of formulas from documents, coupled with standardized workflows, greatly reduced manual effort and error rates across the team.
Ease of use. The platform requires no advanced technical skills, making it accessible to a broad range of professionals. “The fact that it has a simple interface doesn’t mean it’s not good. Otherwise: with just a few clicks, you understand what to do to save and typeset formulas”, affirms Curci.
Flexibility and reusability. Formulas can be adapted to new design preferences with minimal effort, reducing rework.
Support for digital formats. Built-in MathML export facilitates the production of reflowable, accessible digital textbooks.
Collaborative customer service. The collaboration with Wiris has enabled Mondadori Education to resolve technical challenges like spot color management, overprinting, and font compatibility, ensuring consistent output across print and digital.
Cross-department adoption. MathType is used not only by in-house editorial teams but also by all external layout professionals who contribute to Mondadori Education’s math formula typesetting publications. Its status as a shared standard enables a smooth production chain.
Future-proofing. Despite working with older machines to maintain compatibility, Curci and his team are eagerly awaiting the new MathType release. The goal: support newer systems while maintaining continuity.

Looking Ahead Together

We’re entering a new era of innovation, driven by the evolution of our products and the needs of the STEM community. At Wiris, we’re actively working on meaningful improvements of MathType to better support today’s editorial and educational challenges. And we’re not doing it alone, as Mondadori Education and Pietro Curci continue to be by our side, offering their insight, testing new features, and helping us shape what’s next.

For Curci, it’s not just about modernization, it’s about continuity: “I’m not looking for glory” he says. “What I care about is sharing knowledge and ensuring that future generations can build on what we’ve created. Experience is meant to be passed on, not buried”.

Mondadori Education’s relationship with MathType is not just about software: it’s about editorial integrity, long-term thinking, and the power of collaboration. “I’ve worked closely with Wiris for years. I’ve seen how they listen. This isn’t just about Mondadori Education: it’s about keeping a shared legacy alive across the publishing world”. “If one day we had to stop using MathType, it would be a significant loss”.

Interested in MathType? Get in touch.

Uncategorized

Teaching Math Online: Transforming Education with Wiris

Post author By Aida Alsina
Post date July 18, 2025

Teaching math online is redefining the educational landscape. The emergence of advanced digital tools has empowered educators to deliver personalized, flexible learning experiences. Among these innovations, innovative online math teaching methods are crucial in enhancing student engagement, knowledge retention, and academic performance. This article explores these transformative strategies and highlights how Wiris enables educators to implement them effectively and efficiently.

Key Trends in Online Math Teaching: Prioritizing Personalization, Engagement, and Flexibility

In an increasingly digital and dynamic educational landscape, modern online math teaching strategies are evolving to address the diverse needs of today’s learners. The focus is no longer solely on content delivery; it has shifted towards creating learning environments that foster personalization, maximize student engagement, and offer flexibility to accommodate different learning styles and paces.

The most prominent and impactful trends in teaching math online today include:

Flipped classrooms: The flipped classroom model transforms the traditional educational paradigm by moving direct instruction outside of the classroom -typically through videos, readings, or online content- and reserving classroom time for active learning. This approach fosters deeper understanding through discussions, collaborative problem-solving, and interactive exercises in math education. Students engage with material at their own pace before class and apply their knowledge during in-person or synchronous online sessions.
Microlearning: Microlearning involves delivering information in small, focused segments that are easier to digest and retain. Rather than overwhelming students with lengthy, complex lessons, microlearning breaks content into concise, manageable units. In innovative online math teaching, this method proves highly effective, as it reduces cognitive overload and enables students to achieve mastery one concept at a time.
Personalized learning: Personalized learning leverages technology to tailor educational experiences to the unique needs, skills, and interests of each student. In the context of online math teaching, this approach allows educators to adapt instruction dynamically, enabling students to progress at their own pace. It ensures that learners receive the right level of support and challenge, enhancing motivation and academic performance.

Wiris solutions, including WirisQuizzes and LearningLemur, represent online tools for teaching math online that operationalize these methodologies, enabling educators to develop dynamic assessments and tailored learning paths for their students.

Real-World Applications: How These Online Math Teaching Strategies Benefit Students

Adopting personalized learning, microlearning and flipped classroom strategies equips students with competencies critical for real-world success. These methodologies not only boost academic outcomes but also nurture skills crucial for thriving in digital and collaborative professional environments.

Through innovative online math teaching methods, educators are fostering the development of vital skills such as problem-solving, critical thinking, and self-directed learning, which are capabilities increasingly demanded in STEM industries and the future workforce.

Flipped Classrooms: Learning by Doing Instead of Memorizing

The flipped classroom model fosters student autonomy by shifting content delivery outside the classroom and reserving in-person sessions for collaborative, higher-order learning activities. Instead of passively listening to lectures, students engage with preparatory materials —such as videos or readings— at their own pace and use classroom time to apply concepts through problem-solving and discussion.

This method promotes critical thinking, deeper understanding, and active participation. It also supports diverse learning styles and encourages students to take greater responsibility for their learning. By transforming the classroom into a dynamic, interactive environment, the flipped model builds key competencies such as communication, collaboration, and analytical skills.

Benefits of the Flipped Classroom Model

These are the main benefits of the Flipped Classroom Model, a teaching approach that is increasingly gaining traction in modern educational methods:

Assign dynamic, preparatory quizzes to prime students for in-class activities. Assigning dynamic, preparatory quizzes ensures students engage with key concepts before class. This preparation allows for more effective in-class sessions focused on applying knowledge rather than covering basics. Tools like WirisQuizzes and LearningLemur can support you in developing these dynamic preparatory quizzes tailored to your learners’ needs.
Foster interactive, discussion-based classroom environments. With prior exposure to the material, class time can be devoted to discussions and collaborative problem-solving. This shift enhances critical thinking and promotes deeper understanding through active dialogue.
Promote active participation and collaborative learning dynamics. Flipped classrooms encourage students to actively participate and collaborate with peers. Working in teams and engaging in problem-solving activities builds not only academic skills but also essential competencies like communication and teamwork.

girl studing online

The Power of Microlearning: Quick Lessons for Better Retention

Microlearning is gaining traction as an effective strategy in online math teaching. This method decomposes complex concepts into manageable units, promoting deeper understanding and better long-term retention.

With WirisQuizzes and LearningLemur, educators can design brief, targeted quizzes that reinforce core concepts efficiently. The immediate feedback mechanisms facilitate real-time learning corrections. These micro-assessments exemplify innovative online math teaching approaches that reduce cognitive load and improve learning efficacy. This tool streamlines microlearning by enabling the creation of interactive, goal-oriented quizzes.

WirisQuizzes incorporates a feature that enhances microlearning by providing tailored feedback for open-ended math questions. It supports three main types of feedback: suggestive feedback, which guides students toward discovering solutions independently; confirmatory feedback, which reinforces correct answers and boosts confidence; and corrective feedback, which identifies mistakes and provides the correct solution. This immediate, adaptive feedback fosters critical thinking and ensures efficient, focused learning, aligning perfectly with microlearning principles.

feedback with wirisquizzes

Personalized Learning: Delivering Tailored Educational Experiences

Personalized learning is a cornerstone of modern educational methodologies, particularly in teaching math online. It leverages technology to customize educational experiences according to the unique needs, skills, and learning speeds of individual students.

WirisQuizzes and LearningLemur are central to enabling this level of personalization:

WirisQuizzes, oriented to higher education, allows teachers to design sophisticated quizzes incorporating mathematical expressions, graphical representations and dynamic text-based responses. Its advanced randomization and evaluation capabilities generate unique assessments for the students, promoting practice through varied and individualized problem sets.
LearningLemur, oriented to K-12 students and seamlessly integrated with Google Classroom, offers a comprehensive platform for customizable quizzes, automated grading, and personalized feedback. It not only saves educators valuable time but also fosters student engagement and mastery. The platform’s extensive library of adaptable exercises and detailed analytics empowers educators to monitor student progress and intervene when necessary, further enhancing personalized learning. In addition, LearningLemur now incorporates an AI math question generator that understands your needs and generates ready-made quizzes in seconds. It’s designed to address one of the most common pain points for educators: how to start creating math assessments efficiently without sacrificing quality.

learning lemur ai questions

What truly differentiates Wiris’ tools from others is their capacity to mathematically interpret any answer, apply rigorous mathematical logic to personalize feedback, and define random variables using advanced algorithms. These capabilities empower educators to offer more precise and responsive learning experiences, ensuring that each student progresses at their optimal pace and receives support tailored to their specific learning trajectory.

By integrating these solutions, educators can create adaptive learning environments where technology dynamically adjusts to student needs, providing instant feedback and continuously aligning educational content with individual learning goals.

Embracing the Future of Education with Wiris

The digital transformation of education demands agile, student-centric teaching methodologies. Teaching math online requires sophisticated tools, and Wiris stands at the forefront, delivering solutions that enable educators to design personalized, interactive learning experiences.

Enhance your online teaching strategy: start using WirisQuizzes today and experience the benefits of next-generation online tools for teaching math online.

Try WirisQuizzes now

Uncategorized

How Online Math Learning with Wiris Transformed UNED

Post author By Aida Alsina
Post date June 25, 2025

Breaking Barriers in Online Math Learning with Wiris

In the ever-evolving landscape of online education, ensuring that mathematical and scientific content is easy to create, share, and evaluate is a challenge.

Universidad Nacional de Educación a Distancia (UNED), Spain’s leading distance-learning university, recognized this challenge early on. With thousands of students across various disciplines, UNED sought a robust solution to enhance its teaching and evaluation processes, particularly in mathematics and science-related subjects.

To tackle these challenges, UNED turned to online math learning with Wiris, integrating WirisQuizzes and MathType into their educational workflow. Having been a valued client of Wiris for over 15 years of the company’s 25-year journey, UNED has continuously trusted in Wiris’ math solutions to support its evolving digital education needs. We sat down with Mari Carmen García Llamas, a professor in the Economics and Tourism Bachelor’s Degrees, and Raúl Morales Hidalgo, Head of the E-learning Platform at UNED, to understand how these tools transformed their math teaching and assessment methods.

The Challenge: Teaching Math in a Digital Environment

Before implementing Wiris’ solutions, UNED faced significant obstacles in creating and communicating mathematical content effectively in an online setting.

From a technical perspective, their biggest challenge was integrating a math-editing tool into their custom learning platform. Faculty members struggled with writing mathematical formulas in forums, assignments, and quizzes resulting in a poorer learning experience for students.

From a teaching perspective, professors required an intuitive solution to easily insert mathematical expressions into quizzes and ensure smooth interaction with students.

Carmen explains:

“Without a tool to write mathematical symbols, explaining calculations was a big challenge. Whether it was an integral or an algebraic equation, it was always difficult to pinpoint where a student had made an error.”

Additionally, UNED needed an assessment tool that allowed mathematical expressions throughout a quizz, from problem statements to answer options. The absence of such a tool limited quiz and assignment creation.

The Solution: Enhancing Online Math Learning at UNED with Wiris

To overcome these challenges, UNED explored available solutions and found WirisQuizzes and MathType to be the most comprehensive and well-integrated tools for their needs. Their decision to implement Wiris’ solutions was based on several key factors:

Seamless integration with OpenLMS that they use in-house

UNED initially discovered MathType through faculty recommendations and was particularly drawn to its integration with Microsoft Office. However, since they had a custom in-house platform, they needed a solution that could be fully embedded.

Wiris’ technical team collaborated with UNED to integrate MathType and WirisQuizzes into their platform, ensuring a smooth transition and enhanced functionality.

User-friendly for professors and students

With online math learning with Wiris, professors could now write and edit formulas effortlessly across various platforms, including forums, quizzes, and assignments. This eliminated previous barriers in math-based communication between students and teachers.

Carmen highlights the impact:

“We needed a tool that was just as easy to use for the teacher as it was for the student. Wiris makes it possible to create math-rich quizzes where every question is fully customizable.”

Encouraging Active Learning by Breaking Away from Memorization

One of the standout features of WirisQuizzes is its ability to introduce randomized mathematical expressions into quizzes. This ensures that each student receives a unique version of an exercise, discouraging memorization and promoting active learning. This was highlighted by Carmen when she stated:

“WirisQuizzes allows us to create quizzes where every exercise is unique. The level of flexibility it provides is amazing.”

A welcome surprise: the power of WirisQuizzes

While UNED initially focused on MathType, they soon discovered that WirisQuizzes offered additional benefits. As they expanded their digital assessment strategies, WirisQuizzes proved to be an unexpected but valuable tool in enhancing student engagement and practice opportunities.

Raúl shares his excitement:

“When we started making changes to our platform, we were pleasantly surprised by WirisQuizzes. It felt like an unexpected gift, and it has been an incredibly powerful one.”

The Implementation Process: A Collaborative Approach

To successfully integrate online math learning with Wiris into their learning environment, UNED, along with Wiris’ technical team, followed a structured implementation process:

Understanding institutional needs

UNED’s faculty and technical teams worked with Wiris to assess their specific requirements, particularly the need for platform integration and math-based assessments.

Customization and integration

Wiris’ technical experts customized the tools to align with UNED’s platform requirements, ensuring a smooth user experience. Furthermore, the team at Wiris assisted in resolving any doubts as well as providing tips and training on how to use WirisQuizzes efficiently.

Deployment across OpenLMS

The integration was successfully implemented on OpenLMS, allowing professors to seamlessly create and edit formulas within quizzes and discussion forums.

Learning Math Online with Wiris – The Results

Following the implementation of online math learning with Wiris, UNED experienced measurable improvements in teaching efficiency and student engagement:

Greater flexibility for teachers in math-based quiz creation.
Improved student engagement through randomized exercises.
Seamless math communication in forums and assignments.
Quick technical support ensures smooth day-to-day usage.

Carmen notes:

“Wiris allows us to create diverse quizzes with distinct options, making every assessment dynamic and interactive.”

Students also benefit from interactive, dynamic learning experiences, where every exercise is different, allowing them to practice multiple problem variations in a single topic.

Future Plans: Looking Ahead with WirisQuizzes

After experiencing the benefits of WirisQuizzes, UNED is eager to see how the tool evolves and continues to support its online math learning needs. While it is currently used for continuous self-evaluation, faculty members appreciate its capabilities and will continue integrating it into their teaching workflows.

Carmen shares:

“More than one of my colleagues has reached out to me about the potential of Wiris’ solutions. I believe we are only beginning to explore what’s possible.”

Rounding Off: UNED’s Endorsement of Online Math Learning with Wiris

With over 15 years of using Wiris products, UNED strongly endorses WirisQuizzes and MathType for their ease of use, powerful assessment features, and seamless integration.

Raúl emphasizes:

“We have always recommended Wiris. That’s why we’ve been with you for 15 years already.”

Try Wiris for Your Institution

UNED’s success story showcases how online math learning with Wiris can revolutionize digital math education.

If you’re looking to improve math-based assessments in your institution and want a seamless math-writing experience for students and teachers, don’t delay—contact us today.

Request a Demo Today

Uncategorized

AI for Math: The Smart Way to Create Quizzes Faster

Post author By Aida Alsina
Post date June 12, 2025

Creating engaging and varied math quizzes can be a surprisingly time-consuming task. Teachers often face the dreaded blank page, struggling to come up with fresh problems that match different levels, topics, and student needs. But that’s about to change. With AI for math making its way into classrooms, quiz creation just got a powerful upgrade.

Meet LearningLemur: Your AI Question Generator

LearningLemur is an intuitive math platform integrated with Google Classroom that provides customizable quizzes, automatic grading, and personalized feedback, saving educators time and enhancing student learning. Its extensive library of customizable quizzes and exercises fosters engagement and mastery, while detailed analytics help educators track progress and identify areas for improvement. From simplifying assignment creation to delivering instant feedback, LearningLemur transforms classrooms into dynamic and interactive learning spaces, making math more accessible and engaging for all students.

Now, Wiris has introduced a new feature within LearningLemur: a math question generator that understands your needs and generates ready-made quizzes in seconds. It’s designed to address one of the most common pain points for educators: how to start creating math assessments efficiently without sacrificing quality.

Here’s what LearningLemur’s new AI-powered tool offers:

Describe the type of questions you want.
Receive an instant set of customized math problems.
Edit, refine, and assign them directly to your students.

Forget about starting from scratch. This tool helps you work smarter, not harder, all within a platform that is intuitive and easy to navigate, even for teachers with limited tech experience.

How does it work?

Using this tool is simple and straightforward. Teachers input the number of questions, select the question type (e.g., open answer, multiple choice) and finally provide a prompt (e.g., “Make fractions sum problems for students of grade 12. Ask them to be simplified.”).

The AI handles the rest, offering draft content that aligns with your instructions. And because it’s powered by the trusted Wiris correction engine, you maintain full confidence in the mathematical accuracy.

Why This AI Feature Matters for Educators

The LearningLemur AI question generator isn’t just about saving time. It’s designed to help teachers focus on what really matters: pedagogy, clarity, and curriculum alignment. While the AI handles the generation, teachers can shape the output by ensuring pedagogical alignment with curricular goals, adjusting the complexity and style of each question, and refining the language and clarity for the specific group of learners. This tool does not replace your expertise but accelerates your workflow, allowing you to dedicate more time to effective teaching.

Tips for Writing Effective Prompts

Crafting the right prompt is crucial to getting the most out of the LearningLemur AI for math tool. Think of it as briefing a colleague or delegating to a student teacher. Be clear, be specific, and include the following:

Specify the exact math topic you want to assess in your students. For example, indicate whether you want exercises on fractions or polynomials.
Define the educational level or age of your students to tailor the difficulty. Questions should be accessible yet challenging, matching the knowledge and skills of your learners.
Add any constraints. If you have specific requirements, such as simplifying answers or using decimals only, be sure to include them. This ensures the generated questions meet your pedagogical or exam criteria.
Optionally, use word problems to add context and generate relatable scenarios. Adding context or real-life situations makes problems more engaging and easier to understand for students. For instance, framing a problem in the context of shopping, travel or science helps connect math to everyday life and increases motivation.

Example Prompts

“Create 6 word problems on solving linear equations for Grade 9. Include at least one with negative coefficients and require students to simplify x.”

“Create 10 questions on simplifying algebraic expressions for 11-year-old students. Include at least one question involving the distributive property and another with factoring.”

“Create 5 questions for first-year university math students on calculating the rank of a matrix using elementary row operations.”

Use Cases in the Real Classroom

The LearningLemur math question generator adapts across levels and contexts:

For daily practice, generate variations to reinforce a concept.
For formative assessment, tailor difficulty and format.
For homework, instantly provide differentiated sets by level.
For exam prep, create question banks by topic or skill.

And since you can edit anything, it integrates seamlessly into any teaching style.

Diverse Learning Needs: Easily Tailor Content to Students’ Needs

From the teachers’ perspective, LearningLemur offers great flexibility, as educators with limited time or resources in creating math problems can now generate high-quality content more quickly. These advantages are particularly evident for teachers managing large classes, as they can personalize content while reducing preparation time.

Additionally, LearningLemur enables teachers to address the diverse needs of their students by creating customized quizzes and exercises tailored to different skill levels and learning requirements. Teachers can also assign targeted homework tasks, allowing students to strengthen specific competencies where they may need additional support.

Empowering Teachers Through Intelligent Automation

AI for math isn’t about replacing educators: it’s about empowering them. LearningLemur is a clear example of how AI question generators can reduce friction in the creative process while leaving full pedagogical control in teachers’ hands.

Whether you’re battling writer’s block or trying to generate multiple versions of a quiz quickly, this tool gives you a solid head start.

Try the AI of LearningLemur now