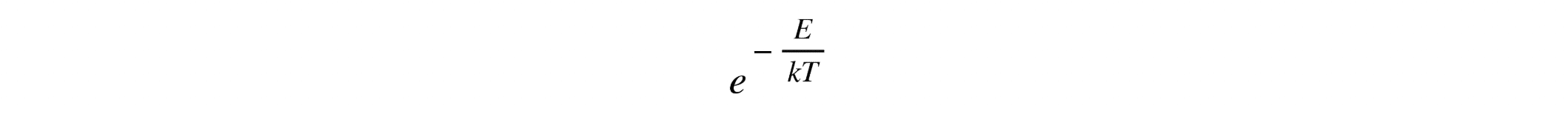When discussing fundamental mathematical constants, pi often takes the spotlight. However, another number, equally vital yet less celebrated, is Euler’s number e. Known simply as e, this constant appears in countless mathematical contexts and real-world applications. In this article, we will explore the origin, properties, and applications of e, positioning it as an indispensable tool in the worlds of mathematics, science, and finance.

What Is Euler’s Number e?

Euler’s number e is an irrational and transcendental number, approximately equal to 2.71828. It serves as the base of natural logarithms and arises naturally in various growth processes and limit calculations.

The Origin of e: A Practical Example

Consider the following real-life scenario: Imagine a bank offering a 100% annual interest rate on a principal investment of 1€. If interest is compounded once at the end of the year, you would have 2€. However, if the bank compounds interest semiannually at 50% every six months, the calculation changes:

After six months: 1€ × 1.5 = 1.5€
After another six months: 1.5€ × 1.5 = 2.25€

Now, let’s divide the year into three periods of four months each, applying an interest rate of 33.33% every four months:

After four months: 1€ × 1.33 = 1.3333€
After eight months: 1.3333€ × 1.3333 ≈ 1.7777€
After twelve months: 1.7777€ × 1.3333 ≈ 2.3703€

So, if you receive infinite payments, will you have infinite money? Unfortunately, the answer is no. As the frequency increases -from quarterly to monthly, to daily, and beyond- the final amount approaches a limit. The formula to calculate this is:

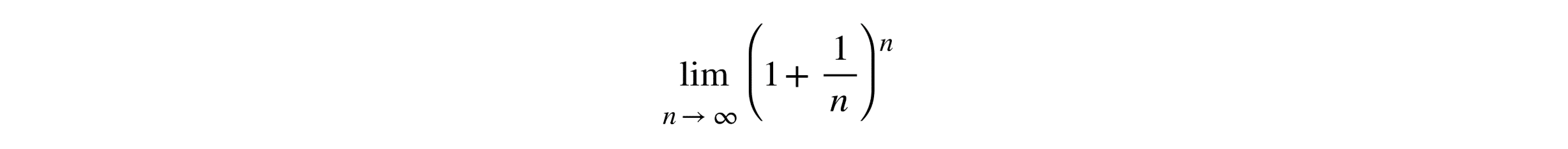
mathtype formula Image created with Wiris’ MathType

As n approaches infinity, the value converges to e. This simple yet powerful example demonstrates the natural emergence of e in exponential growth, explaining its foundational role in continuous compounding interest models.

Fundamental Properties of e Number

Irrationality: e cannot be expressed as a simple fraction.
Transcendence: e is not a root of any non-zero polynomial equation with rational coefficients.
Infinite Series: e can be represented as the sum of the infinite series:

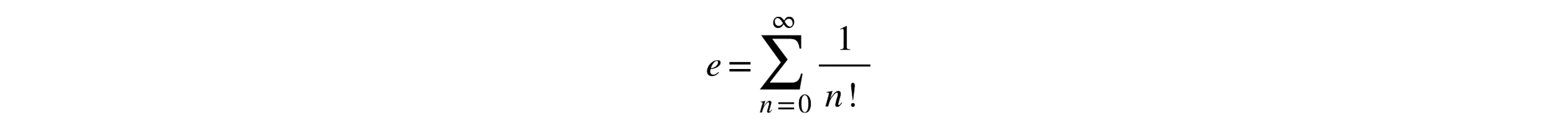
equation with mathtype

Image created with Wiris’ MathType

Natural Logarithm Base: The function uses e as its base, integral to calculus and natural growth models.
Euler’s Identity: Considered one of the most beautiful equations in mathematics:

eⁱ^π+ 1 = 0

This equation elegantly connects five fundamental mathematical constants: 0, 1, e, i, and π.

Applications Across Disciplines

Euler’s number e is not only a fundamental constant in pure mathematics but also plays a pivotal role in a range of practical applications across various scientific and technological fields. From modeling growth processes to risk management, e is indispensable in understanding and predicting complex phenomena.

In Mathematics

Calculus: Euler’s number is central to calculus, particularly in the context of exponential growth and decay. One of the most important properties of e is that the derivative of the function e^x is e^x itself. This unique property makes it extremely useful in solving differential equations that describe dynamic systems, such as population growth, radioactive decay, and heat transfer. It simplifies the analysis of these systems because the function is self-replicating under differentiation.
Complex numbers: Euler’s formula, e^ix = cos(x) + isin(x), is one of the most profound equations in mathematics, linking exponential functions with trigonometric functions. This relationship is crucial in fields like electrical engineering and signal processing, where it simplifies the analysis of oscillating systems and waveforms. It allows for a more intuitive understanding of rotations and oscillations in the complex plane.

In Physics

Radioactive decay: The process of radioactive decay follows an exponential law, which can be modeled using e. The amount of a radioactive substance remaining after a certain period is given by the equation N(t) = N₀e^λt, where N(t) is the amount of substance at time t, N(t) is the initial amount, and λ is the decay constant. This model is used to predict the behavior of radioactive materials over time, which has applications in medicine (e.g., radiology), archaeology (e.g., carbon dating), and nuclear physics.
Thermodynamics: In thermodynamics, the Boltzmann factor (see image below) is essential for determining the probability of a system being in a particular energy state, where 𝐸 is the energy, 𝑘 is the Boltzmann constant, and 𝑇 is the temperature. This exponential relationship is vital in understanding systems in equilibrium, such as the distribution of particles in gases or the behavior of molecules in biological processes.

In Economics and Finance

Continuous compounding: One of the most common uses of e is in the calculation of continuously compounded interest. If interest is compounded continuously rather than at discrete intervals, the formula for the accumulated value of an investment becomes A = Pe^rt, where 𝑃 is the initial investment, 𝑟 is the interest rate, and 𝑡 is the time in years. This formula highlights how the frequency of compounding approaches a limit, with e representing the limit as compounding becomes continuous. It is fundamental in understanding the long-term growth of investments and savings.
Risk models: Financial models such as the Black-Scholes model for option pricing rely heavily on e to account for the stochastic nature of asset prices. The formula for option pricing involves exponential functions to model how the price of an option evolves over time. e also plays a key role in various risk models, including Value at Risk (VaR) calculations, where it helps quantify the likelihood of extreme losses in investment portfolios.

In Technology

Algorithms: Euler’s number is used in algorithmic analysis, particularly when analyzing the performance of algorithms that exhibit exponential growth. For instance, certain random processes and algorithms, such as the analysis of QuickSort (a widely used sorting algorithm), can involve e. Specifically, in probabilistic algorithms and complexity theory, e appears in the expected running time of algorithms, as they often follow exponential distributions or involve recursive calculations that converge to e.
Machine learning and data science: In machine learning, e is frequently involved in algorithms that model growth processes or in optimization algorithms that use exponential decay to adjust parameters over time. For instance, in gradient descent, which is used to find the minimum of a function, learning rates may decay exponentially based on e to optimize performance and prevent overshooting.

In Biology and Medicine

Population growth: One of the most well-known real-world applications of e is in modeling population growth. When populations grow in ideal conditions (without external limitations), the number of individuals follows an exponential growth curve, which is modeled by the equation, P(t) = P₀e^rtwhere 𝑃(𝑡) is the population at time 𝑡, P₀ is the initial population, and 𝑟 is the growth rate. This principle is not only relevant to ecology but also helps in understanding the spread of diseases in epidemiology.
Pharmacokinetics: The exponential decay model is also used in pharmacokinetics, which studies how drugs are absorbed, distributed, metabolized, and excreted by the body. The concentration of a drug in the bloodstream over time often follows an exponential decay, and the parameter governing the decay is related to e. This helps in determining dosing schedules for medications to ensure therapeutic levels are maintained without causing toxicity.

Visualizing Euler’s Number e with Wiris’ Digital Tools

As digital solutions advance, tools like MathType and CalcMe empower users to work effortlessly with e and other complex mathematical expressions. Whether you’re a researcher, educator, or professional, integrating these Wiris’ technologies into your workflow ensures precision and efficiency.

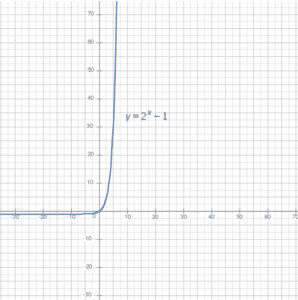
For instance, to deepen the understanding of e’s behavior, one can visualize the limit expression

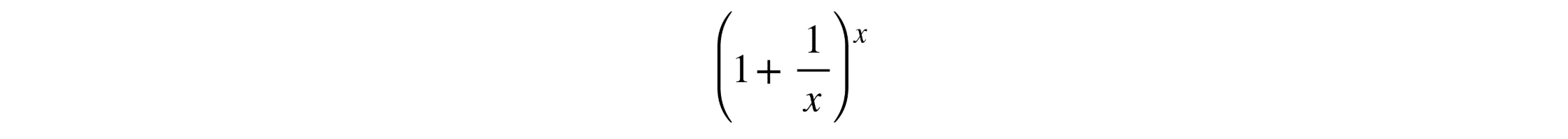
equation editor

using graphing tools such as CalcMe, a Computer Assisted System (CAS) for algebraic manipulation that allows complex mathematical calculations to be carried over in a self-contained, fast and intuitive way. As increases, the graph approaches the value of number e, offering an intuitive graphical demonstration of this mathematical limit.

Additionally, MathType, the world’s leading equation editor that allows you to write math notation as easily as you write text, enables seamless insertion of complex mathematical expressions into documents and web content, ensuring clarity and precision.

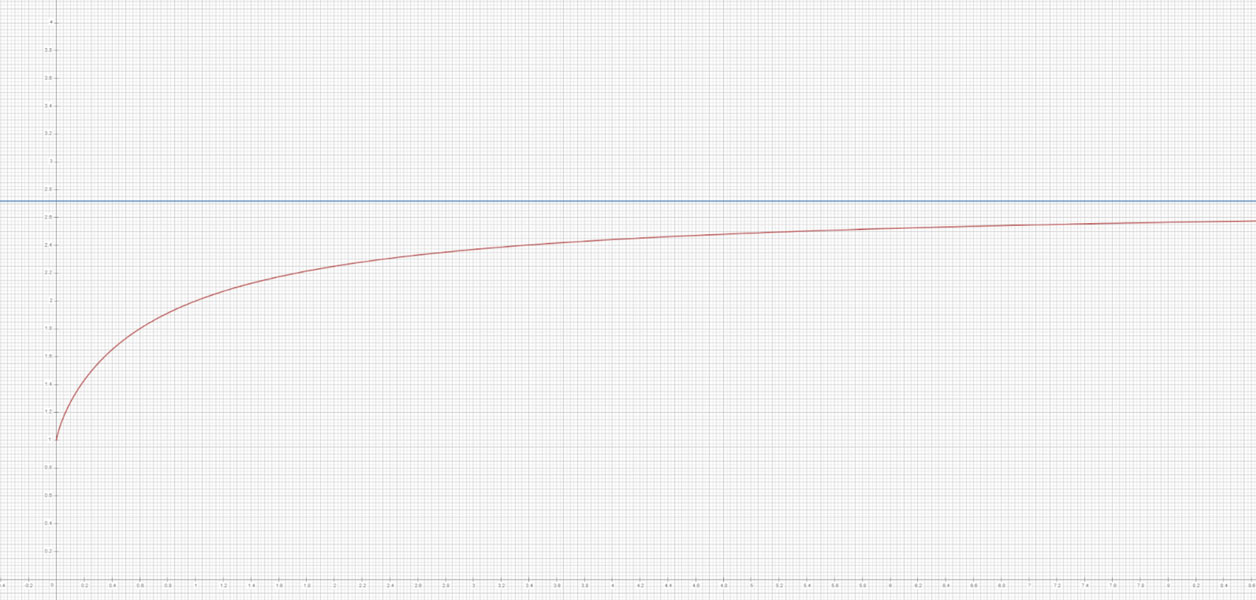
number e graphic

Graph showing the function (1+1/x)^x in red, approaching the value of e in blue.

Perfect for students, teachers, editors, and technical writers, MathType streamlines the creation of high-quality technical and scientific content across various platforms.

For seamless handling of mathematical expressions and visualizations, consider incorporating both MathType and CalcMe into your digital toolkit.

Write your e number equations here!

Towers of Hanoi: A Math and Programming Challenge

The Towers of Hanoi is one of the most iconic puzzles in the field of mathematics and computer science. With its simple structure and transparent rules, this problem has captivated mathematicians and amateurs alike, making it an intriguing challenge since its creation.

According to the legend, the Towers of Hanoi were conceived by a group of monks in an ancient temple in India. In the center of this temple, three golden pillars stood, upon which rested 64 disks of various sizes, arranged in the first pillar in an orderly fashion: the largest disk at the base, with progressively smaller disks stacked on top, until reaching the smallest disk, placed at the top.

The monks’ objective was to move all the disks from the first pillar to the third, using the central pillar as an auxiliary. To accomplish this task, they had to follow a strict set of rules:

Only one disk can be moved at a time.
A disc can never be placed on top of a smaller disc.

Legend says that when all the disks were correctly transferred to the last pillar, the world would come to an end. However, how close is the end of the world, really? How long would it take to complete this challenge?

This challenge was officially introduced by the French mathematician Édouard Lucas in 1883 as part of his research in number theory and quickly became a popular problem.

Next, we will analyze the solution of this problem from a mathematical perspective, breaking down its key principles and explore how it transforms into an interesting programming challenge.

Recursion as a Solution to the Puzzle

The challenge of the Towers of Hanoi is not only in moving the disks from one pillar to another following the strict rules but also in calculating how many moves are needed to solve the problem of moving n disks from the origin pillar to the destination pillar.

The most efficient way to approach this problem is through recursion, a fundamental technique in programming. Recursion allows the problem to be divided into smaller subproblems, where the solution of each subproblem leads to the solution of the original problem.

In the case of the Towers of Hanoi, recursion applies naturally, and we can divide the problem of moving n disks into three steps:

Move the first n – 1 disks from the origin pillar to the auxiliary pillar, using the destination pillar as the auxiliary.
Move the largest disc (the disc n) from the origin pillar to the destination pillar.
Move the n – 1 disks from the auxiliary pillar to the destination pillar, using the origin pillar as an auxiliary.

We can repeat this pattern recursively, reducing the number of discs with every step until we reach a base case where only one disk remains, which we just directly move.

In mathematical terms, the minimum number of moves to solve the problem with n disks equals the number of moves needed to solve it for n – 1 disks, plus one to move the largest disk, plus the number of moves needed to solve it for n – 1 disks again. This formula yields the result:

TH( n ) = TH( n – 1 ) + 1 + TH( n – 1 ) = 2TH( n – 1 ) + 1

Where TH( n ) represents the number of moves needed to solve the problem with n disks.

From the above formula, we will substitute each TH( i ) by its corresponding expression until we reach TH( 1 ) . Then, we will replace TH( 1 ) by 1, since, with only one disc, it is possible to move it directly to the destination pillar, which justifies that the minimum number of moves in this case is 1.

Let’s see the expression developed:

We first substitute TH( n – 1 ), and we obtain:

TH( n ) = 2TH( n – 1 ) + 1

TH( n ) = 2( 2TH( n – 2 ) + 1 ) + 1 = 2²TH( n – 2 ) + 3

Now we substitute TH( n – 2 ):

TH( n ) = 2²TH( n – 2 ) + 3

TH( n ) = 2²( 2TH( n – 3 ) + 1 ) + 3 = 2³TH( n – 3 ) + 7

If we continue substituting in this way, we will arrive at a general formula:

TH( n ) = 2^k TH( n – k ) + (2^k – 1)

Where k is the number of steps backward in the recursion.

For k = n – 1 we arrive at TH( 1 ), the base case:

TH( n ) = 2²TH( n – 2 ) + 3

We know that TH( 1 ) = 1, then we obtain:

TH( n ) = 2^{n – 1} · 1 + ( 2^{n – 1} – 1 ) = 2ⁿ – 1

We have shown that the number of moves needed to solve the Towers of Hanoi with n disks is:

TH( n ) = 2ⁿ – 1

Solving the Puzzle Using Mathematical Induction

Another way to approach the solution to the Towers of Hanoi puzzle is to use mathematical induction, a technique used to prove that a statement is true for all natural numbers, based on two fundamental steps: the base case and the inductive step.

In this case, the goal is to show that to move disks from the first pillar to the third pillar, 2ⁿ – 1 moves are required. Let’s break this process down with a demonstration by induction.

Base case:

Suppose we have only one disk. In this scenario, it is clear that only one move is needed to move the disk from the source abutment to the target abutment. That is, for n = 1, the number of moves required is 2¹ – 1 = 1, which is true.

Inductive step:

Now, suppose that the statement is true for n = k, i.e., that to move k disks requires 2^k – 1 moves. What we must prove is that the statement is also true for n = k + 1.

To move k + 1 disks, we first need to move the upper disks from the origin pillar to the auxiliary pillar, using the destination pillar as an auxiliary. According to our inductive hypothesis, this will take 2^k – 1 moves.

Next, we move the larger disk (the disk k + 1) from the origin pillar to the destination pillar, which requires just 1 move.

Finally, we move the k disks from the auxiliary pillar to the destination pillar, using the origin pillar as an auxiliary, which will also take 2^k – 1 moves, according to our inductive hypothesis.

Therefore, the total number of moves required to move k + 1 disks is:

(2^k – 1) + 1 + (2^k – 1) = 2^k+1 – 1

Thus, we have shown that if the statement is true for n = k, it is also true for n = k + 1.

As we have observed, it is true for 1. By mathematical induction, we can conclude that for n disks, the minimum number of necessary moves is 2ⁿ – 1.

Going back to the legend, if the monks were extremely fast and could move a disk in just one second, we could calculate how long it would take to complete the challenge with 64 disks. According to the formula, the total number of moves would be 2⁶⁴ – 1, approximately 18.4 quintillion moves. With each of these taking just 1 second, this gives us 18.4 quintillion seconds. Converting these into years, we get that the total time would be approximately 581.4 billion years. So, if the legend turned out to be true, the end of the world would still be a long way away!

CalcMe formula We note that the function describing the number of moves needed to solve the Towers of Hanoi is exponential, meaning that it grows rapidly as we increase the number of disks. In the following graph, we can visually see how this function spikes, clearly illustrating the exponential growth.

graphic formula

This visual support allows us to confirm, once again, that completing the challenge with 64 discs would take an extraordinary amount of time.

If you liked this mathematical challenge and you were surprised by its solution, don’t hesitate to share this article! And if you dare, test your skills by solving the Towers of Hanoi puzzle: will you manage to move the disks in the exact number of steps? Let us know your experience!