The Fascinating Probability of Sharing a Date

The birthday paradox is a mathematical concept that invites us to challenge our intuition. A paradox, in essence, is a statement or result that, although seemingly contradictory or contrary to common logic, proves to be true when analyzed closely. In the case of the birthday paradox, the scenario is simple but puzzling: how many people must be in a room for the probability of at least two sharing the same birthday to be greater than 50%?

The result will be surprisingly low, but do you dare to answer before you continue reading to reveal the answer?

The most intuitive way to approach the paradox would be to think that it takes at least 183 people, half the days of the year, for the probability of two people sharing the same birthday to be greater than 50%. However, the reality is very different. 

To understand how this probability is calculated, let us recall that the basic formula of any probability consists of dividing the favorable cases by the total cases. 

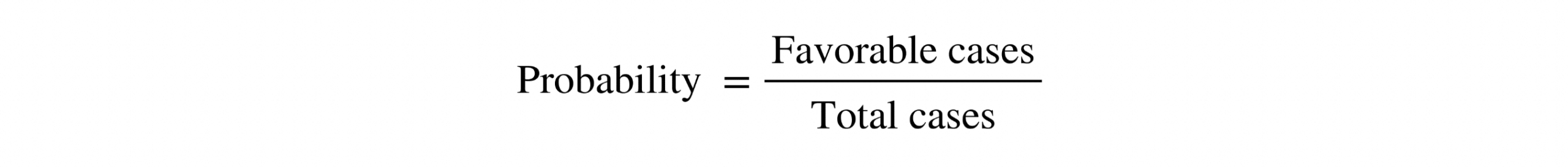
In this case, rather than calculating the probability of a coincidence directly, it is easier to first calculate the probability that no two people share a birthday. After determining this probability, subtracting it from 1 (that is, calculating the complement) gives the probability that at least two people share a birthday.

To calculate the probability that no two people share a birthday, we will proceed constructively, evaluating scenario by scenario.

• If there is only one person in a room, there is no chance that they will share their birthday with someone else since no other people are present. Therefore, the probability that their birthday is unique is 100%, i.e., 365/365.
• Now, if a second person comes in, the probability that their birthday will be different from the first person’s is ​364/365, since there are only 364 days remaining in which they can be born to avoid a coincidence.
• If a third person is added, the probability that their birthday does not match anyone else’s is ​363/365 since there are now two busy days.

Therefore, for n people, all the above conditions must be met simultaneously: that the second person does not share a birthday with the first, that the third person does not share a birthday with the previous two, and so on. This implies that the probability that none of the n people share the same birthday is the product of the individual probabilities:

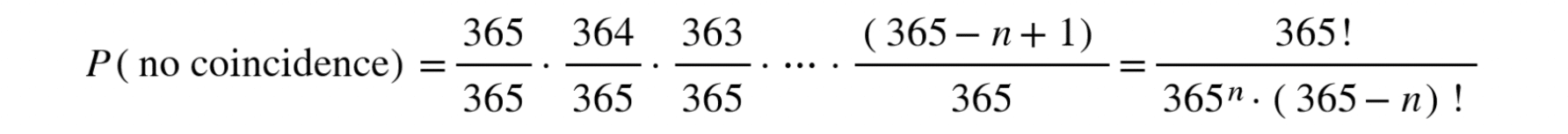
And finally, we obtain:

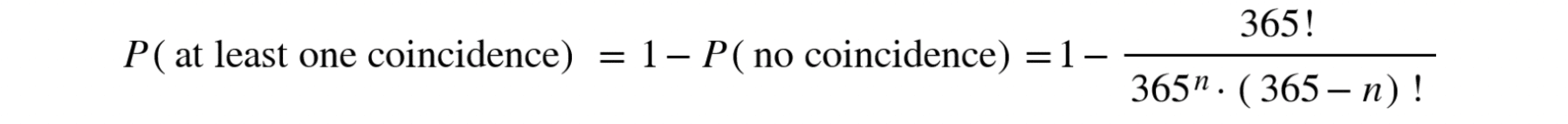
Analyzing probabilities for different values of n

Let us examine the results for different values of n:

• For n=10 we obtain that P (at least one coincidence) = 11,61%
  

This calculation has been created using CalcMe

• For n=15 we obtain that P (at least one coincidence) = 25,03%
• For n=23 we obtain that P (at least one coincidence) = 50,05%
• For n=50 we obtain that P (at least one coincidence) = 96,53%
• For n=60 we obtain that P (at least one coincidence) = 99,22%

As we can see from the examples above, to achieve a probability of more than 50%, only 23 people in the same room are needed. This result may seem surprising, but it makes sense if we consider that with 23 people, 253 different pairs can be formed, and each of these pairs represents a chance for two people to share the same birthday. Even more surprising is that to have a probability greater than 99%, only 60 people are needed, demonstrating how the number of possible combinations grows rapidly with every new person added.

This is the graph of the probability distribution: 

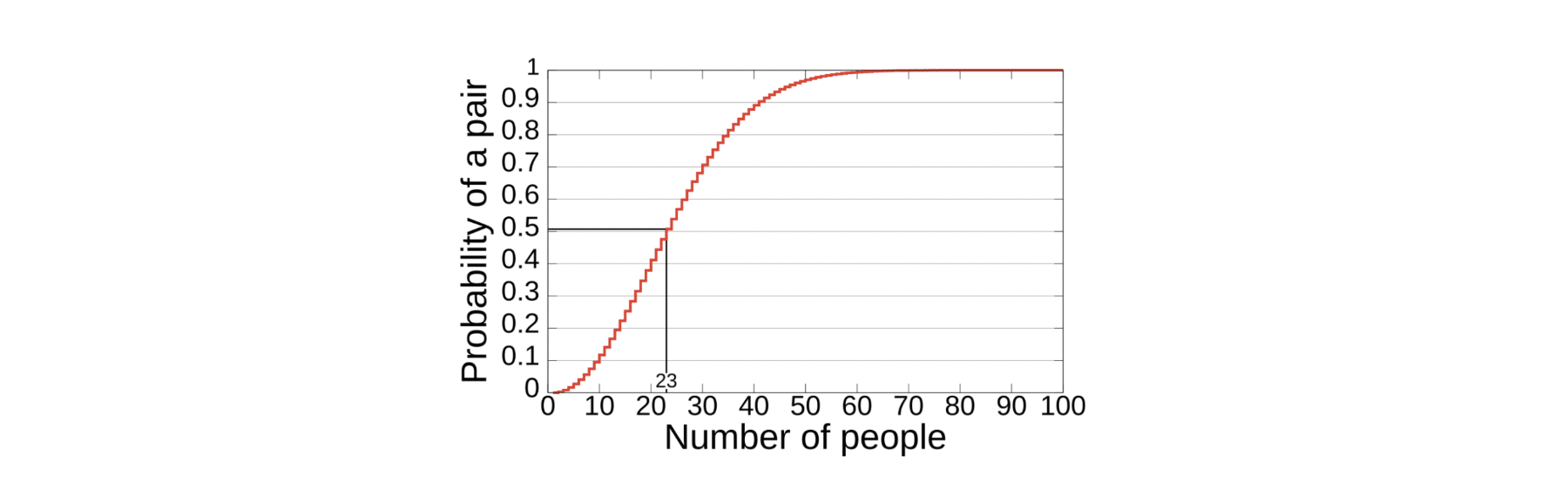
Graph showing the probability of two people sharing a birthday, with the number of people on the X-axis and the probability on the Y-axis, expressed as a percentage.

In contrast, if instead of calculating the probability of coincidence between any pair of people we consider the probability that someone in a room of n people (excluding you) specifically shares your birthday, the calculation is different. This probability is given by: 

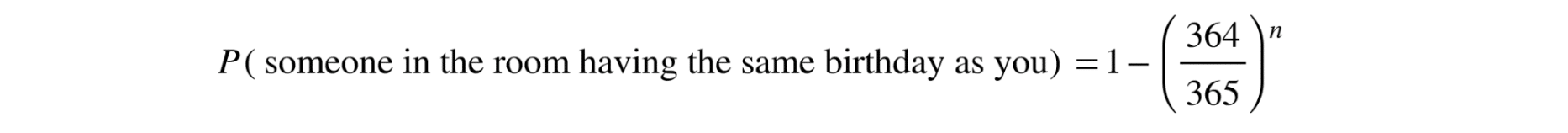
For n = 22, this probability is about 0.059 (5.9%), which is quite low. In fact, there would need to be at least 253 people in the room for this probability to exceed 50%. 

The birthday paradox is a fascinating reminder of how our intuition can fail when confronted with mathematical logic.

Now that you know the birthday paradox and its key concepts, can you calculate the probability that exactly k people within a group of n people share their birthday? We’d love to hear your results in the blog comments! If this article surprised you, share it with your friends so that they can learn more about this mathematical paradox. What’s more, if you’re interested in trying these calculations for yourself, have a look at CalcMe.

 

Try CalcMe