Towers of Hanoi: A Math and Programming Challenge

The Towers of Hanoi is one of the most iconic puzzles in the field of mathematics and computer science. With its simple structure and transparent rules, this problem has captivated mathematicians and amateurs alike, making it an intriguing challenge since its creation.

According to the legend, the Towers of Hanoi were conceived by a group of monks in an ancient temple in India. In the center of this temple, three golden pillars stood, upon which rested 64 disks of various sizes, arranged in the first pillar in an orderly fashion: the largest disk at the base, with progressively smaller disks stacked on top, until reaching the smallest disk, placed at the top.

The monks’ objective was to move all the disks from the first pillar to the third, using the central pillar as an auxiliary. To accomplish this task, they had to follow a strict set of rules:

1. Only one disk can be moved at a time.
2. A disc can never be placed on top of a smaller disc.

Legend says that when all the disks were correctly transferred to the last pillar, the world would come to an end. However, how close is the end of the world, really? How long would it take to complete this challenge?

This challenge was officially introduced by the French mathematician Édouard Lucas in 1883 as part of his research in number theory and quickly became a popular problem.

Next, we will analyze the solution of this problem from a mathematical perspective, breaking down its key principles and explore how it transforms into an interesting programming challenge.

 

Recursion as a Solution to the Puzzle

The challenge of the Towers of Hanoi is not only in moving the disks from one pillar to another following the strict rules but also in calculating how many moves are needed to solve the problem of moving n disks from the origin pillar to the destination pillar.

The most efficient way to approach this problem is through recursion, a fundamental technique in programming. Recursion allows the problem to be divided into smaller subproblems, where the solution of each subproblem leads to the solution of the original problem. 

In the case of the Towers of Hanoi, recursion applies naturally, and we can divide the problem of moving n disks into three steps:

• Move the first n – 1 disks from the origin pillar to the auxiliary pillar, using the destination pillar as the auxiliary.
• Move the largest disc (the disc n) from the origin pillar to the destination pillar.
• Move the n – 1 disks from the auxiliary pillar to the destination pillar, using the origin pillar as an auxiliary.

We can repeat this pattern recursively, reducing the number of discs with every step until we reach a base case where only one disk remains, which we just directly move.

In mathematical terms, the minimum number of moves to solve the problem with n disks equals the number of moves needed to solve it for n – 1 disks, plus one to move the largest disk, plus the number of moves needed to solve it for n – 1 disks again. This formula yields the result:

TH( n ) = TH( n – 1 ) + 1 + TH( n – 1 ) = 2TH( n – 1 ) + 1

Where TH( n ) represents the number of moves needed to solve the problem with n disks.

From the above formula, we will substitute each TH( i ) by its corresponding expression until we reach TH( 1 ) . Then, we will replace TH( 1 ) by 1, since, with only one disc, it is possible to move it directly to the destination pillar, which justifies that the minimum number of moves in this case is 1.

Let’s see the expression developed: 

• We first substitute TH( n – 1 ), and we obtain: 

TH( n ) = 2TH( n – 1 ) + 1 

TH( n ) = 2( 2TH( n – 2 ) + 1 ) + 1 = 2²TH( n – 2 ) + 3

• Now we substitute TH( n – 2 ):

TH( n ) = 2²TH( n – 2 ) + 3

TH( n ) = 2²( 2TH( n – 3 ) + 1 ) + 3 = 2³TH( n – 3 ) + 7

• If we continue substituting in this way, we will arrive at a general formula:

TH( n ) = 2^k  TH( n – k ) + (2^k – 1)

Where k is the number of steps backward in the recursion.

• For  k = n – 1 we arrive at TH( 1 ), the base case:

TH( n ) = 2²TH( n – 2 ) + 3

We know that TH( 1 ) = 1, then we obtain:

TH( n ) = 2^{n – 1} · 1 + ( 2^{n – 1} – 1 ) = 2ⁿ – 1

We have shown that the number of moves needed to solve the Towers of Hanoi with n disks is:

TH( n ) = 2ⁿ – 1

Solving the Puzzle Using Mathematical Induction

Another way to approach the solution to the Towers of Hanoi puzzle is to use mathematical induction, a technique used to prove that a statement is true for all natural numbers, based on two fundamental steps: the base case and the inductive step.

In this case, the goal is to show that to move disks from the first pillar to the third pillar, 2ⁿ – 1 moves are required. Let’s break this process down with a demonstration by induction.

Base case: 

Suppose we have only one disk. In this scenario, it is clear that only one move is needed to move the disk from the source abutment to the target abutment. That is, for n = 1, the number of moves required is 2¹ – 1 = 1, which is true.

Inductive step: 

Now, suppose that the statement is true for n = k, i.e., that to move k disks requires 2^k – 1 moves. What we must prove is that the statement is also true for n = k + 1.

To move k + 1 disks, we first need to move the upper disks from the origin pillar to the auxiliary pillar, using the destination pillar as an auxiliary. According to our inductive hypothesis, this will take 2^k – 1 moves.

Next, we move the larger disk (the disk  k + 1) from the origin pillar to the destination pillar, which requires just 1 move.

Finally, we move the k disks from the auxiliary pillar to the destination pillar, using the origin pillar as an auxiliary, which will also take 2^k – 1 moves, according to our inductive hypothesis.

Therefore, the total number of moves required to move k + 1 disks is:

(2^k – 1) + 1 + (2^k – 1) = 2^k+1 – 1

Thus, we have shown that if the statement is true for n = k,  it is also true for n = k + 1. 

As we have observed, it is true for 1. By mathematical induction, we can conclude that for n disks, the minimum number of necessary moves is 2ⁿ – 1.

Going back to the legend, if the monks were extremely fast and could move a disk in just one second, we could calculate how long it would take to complete the challenge with 64 disks. According to the formula, the total number of moves would be 2⁶⁴ – 1, approximately 18.4 quintillion moves. With each of these taking just 1 second, this gives us 18.4 quintillion seconds. Converting these into years, we get that the total time would be approximately 581.4 billion years. So, if the legend turned out to be true, the end of the world would still be a long way away!

We note that the function describing the number of moves needed to solve the Towers of Hanoi is exponential, meaning that it grows rapidly as we increase the number of disks. In the following graph, we can visually see how this function spikes, clearly illustrating the exponential growth.

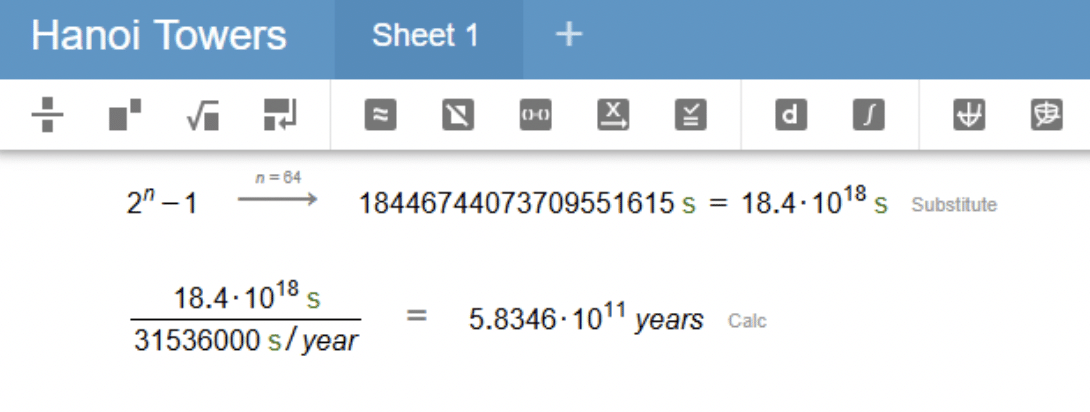
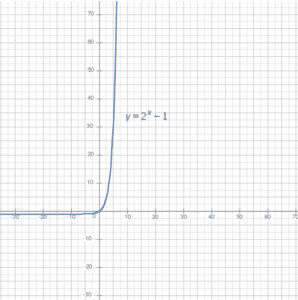
This visual support allows us to confirm, once again, that completing the challenge with 64 discs would take an extraordinary amount of time.

If you liked this mathematical challenge and you were surprised by its solution, don’t hesitate to share this article! And if you dare, test your skills by solving the Towers of Hanoi puzzle: will you manage to move the disks in the exact number of steps? Let us know your experience!