In this article
Rethinking feedback with AI in education
In today’s AI in education landscape, feedback is instant, scalable, and available at the click of a button. A teacher can request ten progressively harder equations or an entire quiz with explanations. A student can paste a math problem into an AI chatbot and receive a step-by-step solution in seconds. This efficiency is game-changing, but it raises an important question: How can real learning be guaranteed?
This article explores how combining classroom AI with peer review fosters deeper mathematical understanding, sharpens communication skills, and transforms students from passive receivers of feedback to active participants in the learning process, as well as how the approach can be put into practice with platforms like LearningLemur, WIRIS Assessment tool powered by AI to support rich, formative feedback in mathematics.
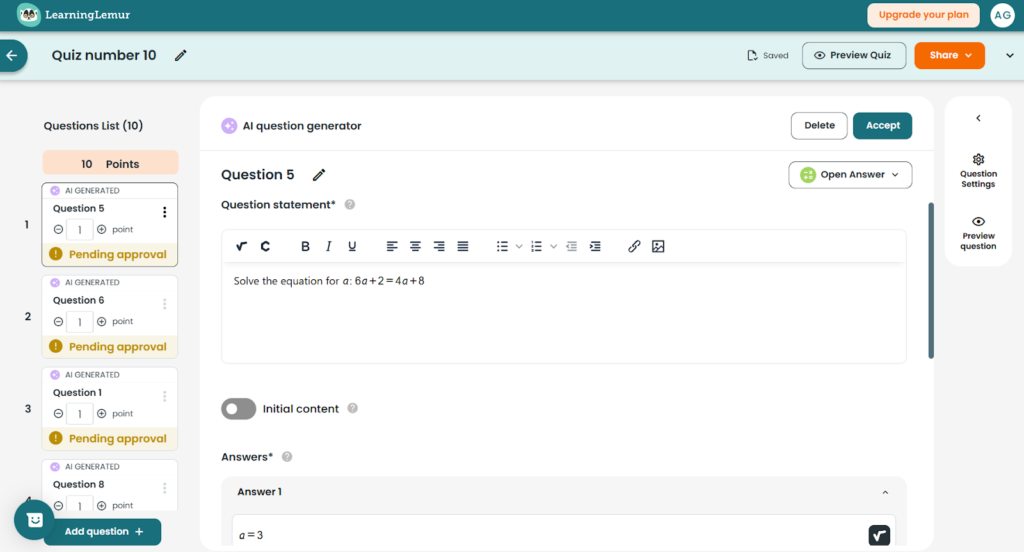
When instant feedback falls short
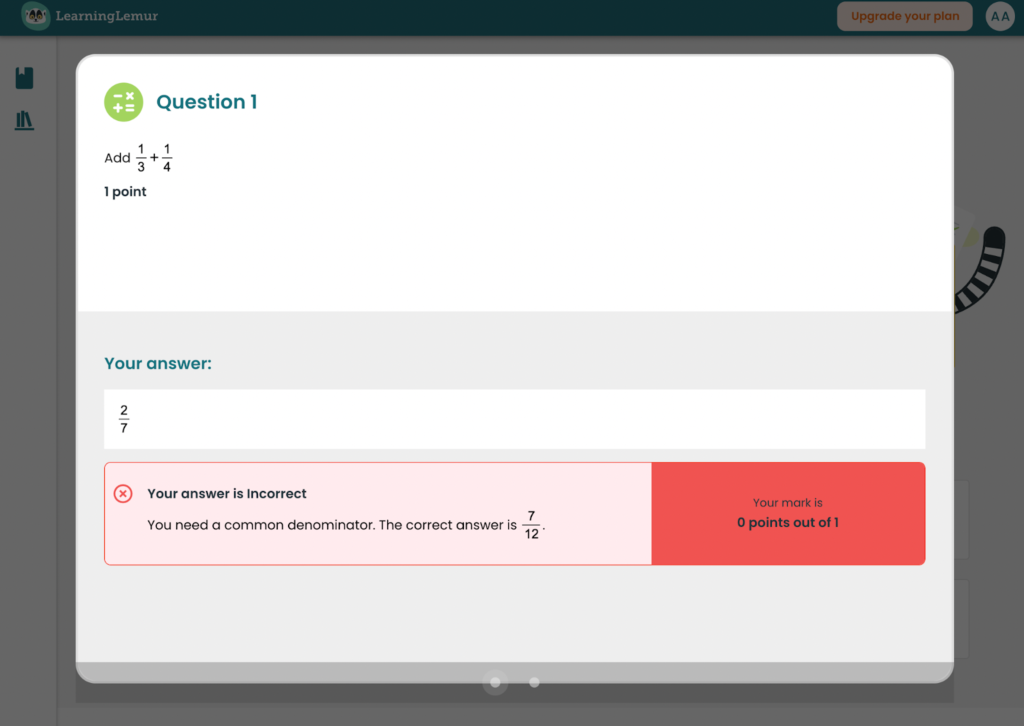
Let’s start with a simple math task: Add one-third and one-quarter. A student answers 1/3 + 1/4 = 2/7. An AI-powered math tool flags it incorrect and offers feedback: “Not quite. Try finding a common denominator. What’s the least common multiple of 3 and 4?”
The student sees this, copies 7/12 (the correct answer), and moves on. But here’s the issue; he never truly confronted his misconception. He thought you could simply add numerators and denominators. The AI offered a clue, but didn’t ensure understanding.
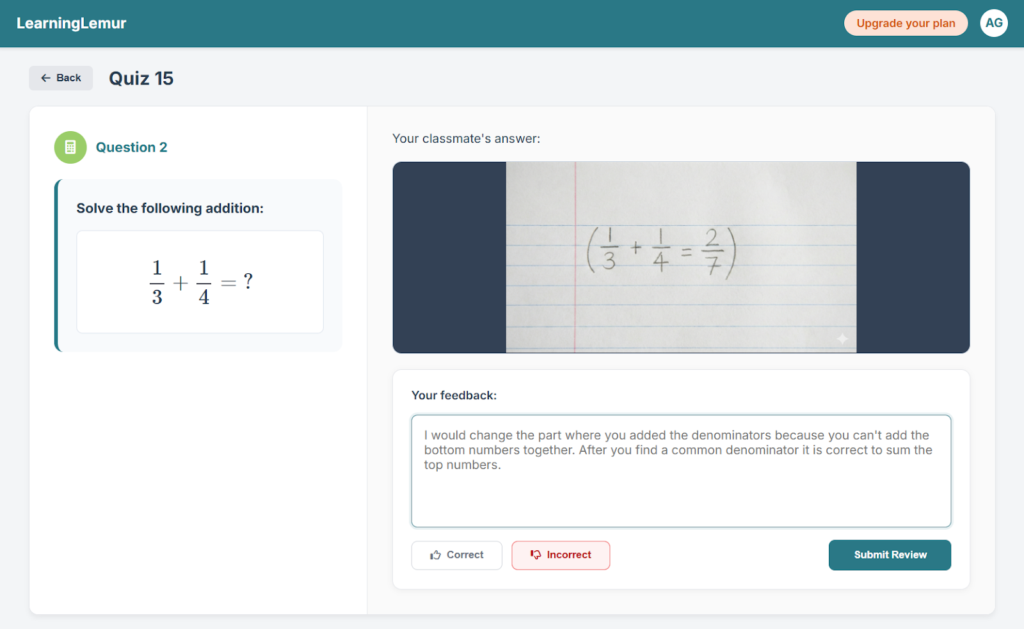
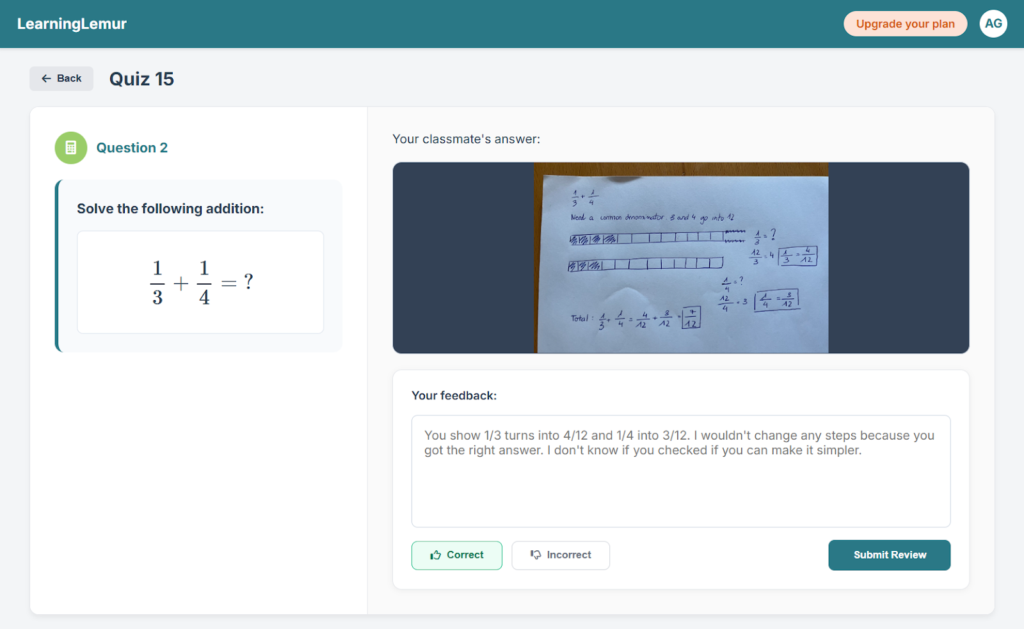
Peer review, on the other hand, opens a different kind of conversation. Imagine another student reviewing this work and writing:
- “You can’t add denominators. Try finding a common one first.”
- “Next time, use 12 as a common denominator, then add.”
Now, the original student is prompted to reflect. She’s being asked to articulate reasoning, not just correct an answer.
Why peer review elevates learning
Math isn’t just about correct answers; it’s about decisions, strategies, and justifications. Peer review encourages students to highlight what’s correct and explain why, to question the steps they find confusing, and to suggest next steps or alternate strategies that could lead to a better solution.
This doesn’t just benefit the student receiving feedback. The reviewer, too, is clarifying and articulating their own thinking. The act of critiquing sharpens metacognition and supports retention.
Here’s an example from a secondary classroom:
- A student solves incorrectly: 2(x – 3) = x + 5
- The AI gives formative feedback: “Check your distribution.”
- The peer reviewer notices a mistake in expanding the brackets and suggests using visual cues (like arrows) to avoid missing steps.
By combining instant hints from classroom AI with structured peer review, students receive a double layer of support: one technical, one human.
A classroom workflow that works
Here’s a four-step model any teacher can use:
- Solve the Task: Students tackle a non-multiple-choice question that requires explanation (e.g., show how you solved 2(x – 3) = x + 5).
- Peer Review: Students are assigned anonymized peer submissions. They review with specific prompts:
- Highlight trusted steps and explain why
- Question unclear reasoning
- Offer one “next time, try…” suggestion
- AI Feedback: After submission, AI gives real-time, formative feedback that offers hints without revealing full solutions.
- Teacher Insight: Teachers gain a rich view, not just who got the answer right, but clusters of misunderstandings and unique strategies.
This model turns AI from an answer key into a coach, and students from answer-checkers into evaluators of reasoning.
Key tips for implementing peer review and AI
Implementing a classroom model that blends AI in education with peer review doesn’t require an overhaul of your teaching strategy. But it does benefit from thoughtful planning and clear routines. Below are practical tips to help educators integrate these tools effectively, ensuring both technologies and students play their roles in deepening mathematical understanding.
- Keep tasks rich but manageable. One good open question is more valuable for peer review than 20 auto-graded items.
- Structure the time. A realistic 50-minute lesson might allocate:
- 20 minutes for solving
- 5 minutes for AI feedback
- 15 minutes for peer feedback
- Set norms for reviewing. Teach students to give specific, kind, and constructive feedback. Focus on the work, not the person.
- Support equity. Use AI in education to generate multiple representations of a problem (visuals, text, examples) to support diverse learners. Peer review then adds multiple voices, making math feel more inclusive.
Real-world benefits of combining AI and peer review
Combining AI in education with peer review offers a range of real-world benefits. For students, it helps develop their communication and critique skills, deepens their understanding of math concepts, and transforms feedback into a two-way dialogue. It also teaches them to recognize that there is more than one correct “math voice” in the classroom.
For teachers, this approach provides richer insight into student thinking, equips them with tools to identify and address misconceptions early, and fosters a more dynamic, student-centered learning environment.
From fast answers to deep understanding: Rethinking math feedback
AI in education offers scale, speed, and convenience. Peer review adds reasoning, collaboration, and reflection. Together, they form a powerful feedback ecosystem that supports more thoughtful, equitable, and effective math learning.
Want to bring this model to your classroom? Start small: one open-ended task, one cycle of peer review, and LearningLemur, your AI-powered math feedback helper. Build from there and watch the transformation.
Share









