Understanding the Power of e number: The Unsung Hero of Mathematics

When discussing fundamental mathematical constants, pi often takes the spotlight. However, another number, equally vital yet less celebrated, is Euler’s number e. Known simply as e, this constant appears in countless mathematical contexts and real-world applications. In this article, we will explore the origin, properties, and applications of e, positioning it as an indispensable tool in the worlds of mathematics, science, and finance.

What Is Euler’s Number e?

Euler’s number e is an irrational and transcendental number, approximately equal to 2.71828. It serves as the base of natural logarithms and arises naturally in various growth processes and limit calculations.

The Origin of e: A Practical Example

Consider the following real-life scenario: Imagine a bank offering a 100% annual interest rate on a principal investment of 1€. If interest is compounded once at the end of the year, you would have 2€. However, if the bank compounds interest semiannually at 50% every six months, the calculation changes:

• After six months: 1€ × 1.5 = 1.5€
• After another six months: 1.5€ × 1.5 = 2.25€

Now, let’s divide the year into three periods of four months each, applying an interest rate of 33.33% every four months:

•         After four months: 1€ × 1.33 = 1.3333€
•         After eight months: 1.3333€ × 1.3333 ≈ 1.7777€
•         After twelve months: 1.7777€ × 1.3333 ≈ 2.3703€

So, if you receive infinite payments, will you have infinite money? Unfortunately, the answer is no. As the frequency increases -from quarterly to monthly, to daily, and beyond- the final amount approaches a limit. The formula to calculate this is:

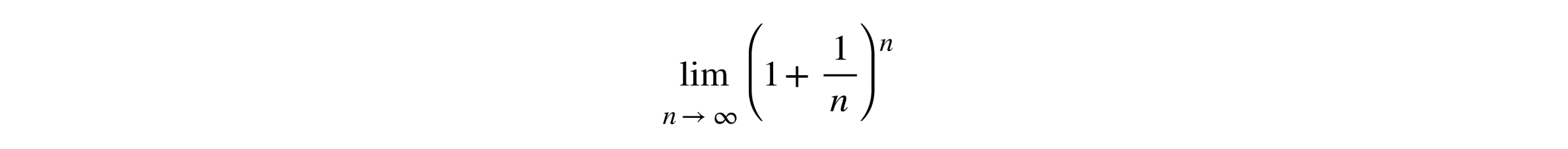Image created with Wiris’ MathType

As n approaches infinity, the value converges to e. This simple yet powerful example demonstrates the natural emergence of e in exponential growth, explaining its foundational role in continuous compounding interest models.

Fundamental Properties of e Number

• Irrationality: e cannot be expressed as a simple fraction.
• Transcendence: e is not a root of any non-zero polynomial equation with rational coefficients.
• Infinite Series: e can be represented as the sum of the infinite series:

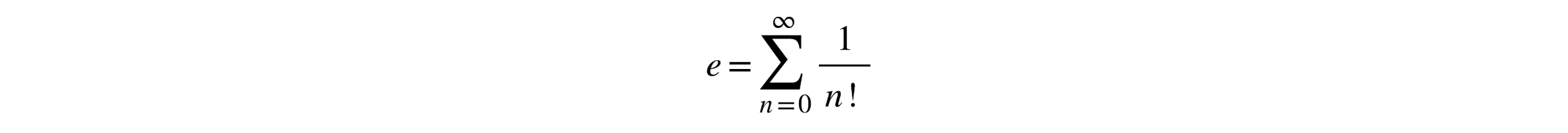
Image created with Wiris’ MathType

• Natural Logarithm Base: The function uses e as its base, integral to calculus and natural growth models.
• Euler’s Identity: Considered one of the most beautiful equations in mathematics:

e^iπ + 1 = 0

This equation elegantly connects five fundamental mathematical constants: 0, 1, e, i, and π.

Applications Across Disciplines

Euler’s number e is not only a fundamental constant in pure mathematics but also plays a pivotal role in a range of practical applications across various scientific and technological fields. From modeling growth processes to risk management, e is indispensable in understanding and predicting complex phenomena.

In Mathematics

• Calculus: Euler’s number is central to calculus, particularly in the context of exponential growth and decay. One of the most important properties of e is that the derivative of the function e^x is e^x itself. This unique property makes it extremely useful in solving differential equations that describe dynamic systems, such as population growth, radioactive decay, and heat transfer. It simplifies the analysis of these systems because the function is self-replicating under differentiation.
• Complex numbers: Euler’s formula, e^ix = cos(x) + isin(x), is one of the most profound equations in mathematics, linking exponential functions with trigonometric functions. This relationship is crucial in fields like electrical engineering and signal processing, where it simplifies the analysis of oscillating systems and waveforms. It allows for a more intuitive understanding of rotations and oscillations in the complex plane.

In Physics

• Radioactive decay: The process of radioactive decay follows an exponential law, which can be modeled using e. The amount of a radioactive substance remaining after a certain period is given by the equation N(t) = N₀e^λt, where N(t) is the amount of substance at time t, N(t) is the initial amount, and λ is the decay constant. This model is used to predict the behavior of radioactive materials over time, which has applications in medicine (e.g., radiology), archaeology (e.g., carbon dating), and nuclear physics.
• Thermodynamics: In thermodynamics, the Boltzmann factor (see image below) is essential for determining the probability of a system being in a particular energy state, where 𝐸 is the energy, 𝑘 is the Boltzmann constant, and 𝑇 is the temperature. This exponential relationship is vital in understanding systems in equilibrium, such as the distribution of particles in gases or the behavior of molecules in biological processes.

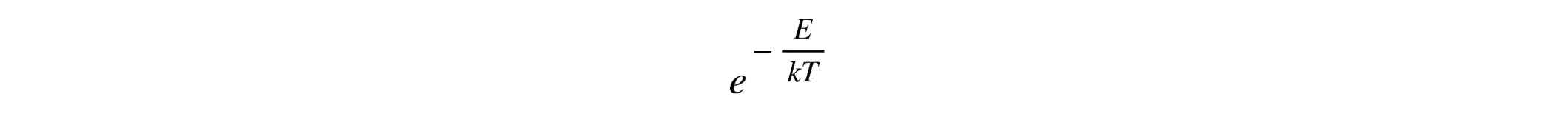
In Economics and Finance

• Continuous compounding: One of the most common uses of e is in the calculation of continuously compounded interest. If interest is compounded continuously rather than at discrete intervals, the formula for the accumulated value of an investment becomes A = Pe^rt, where 𝑃 is the initial investment, 𝑟 is the interest rate, and 𝑡 is the time in years. This formula highlights how the frequency of compounding approaches a limit, with e representing the limit as compounding becomes continuous. It is fundamental in understanding the long-term growth of investments and savings.
• Risk models: Financial models such as the Black-Scholes model for option pricing rely heavily on e to account for the stochastic nature of asset prices. The formula for option pricing involves exponential functions to model how the price of an option evolves over time. e also plays a key role in various risk models, including Value at Risk (VaR) calculations, where it helps quantify the likelihood of extreme losses in investment portfolios.

In Technology

• Algorithms: Euler’s number is used in algorithmic analysis, particularly when analyzing the performance of algorithms that exhibit exponential growth. For instance, certain random processes and algorithms, such as the analysis of QuickSort (a widely used sorting algorithm), can involve e. Specifically, in probabilistic algorithms and complexity theory, e appears in the expected running time of algorithms, as they often follow exponential distributions or involve recursive calculations that converge to e.
• Machine learning and data science: In machine learning, e is frequently involved in algorithms that model growth processes or in optimization algorithms that use exponential decay to adjust parameters over time. For instance, in gradient descent, which is used to find the minimum of a function, learning rates may decay exponentially based on e to optimize performance and prevent overshooting.

In Biology and Medicine

• Population growth: One of the most well-known real-world applications of e is in modeling population growth. When populations grow in ideal conditions (without external limitations), the number of individuals follows an exponential growth curve, which is modeled by the equation, P(t) = P₀e^rt  where 𝑃(𝑡) is the population at time 𝑡, P₀ is the initial population, and 𝑟 is the growth rate. This principle is not only relevant to ecology but also helps in understanding the spread of diseases in epidemiology.
• Pharmacokinetics: The exponential decay model is also used in pharmacokinetics, which studies how drugs are absorbed, distributed, metabolized, and excreted by the body. The concentration of a drug in the bloodstream over time often follows an exponential decay, and the parameter governing the decay is related to e. This helps in determining dosing schedules for medications to ensure therapeutic levels are maintained without causing toxicity.

Visualizing Euler’s Number e with Wiris’ Digital Tools

As digital solutions advance, tools like MathType and CalcMe empower users to work effortlessly with e and other complex mathematical expressions. Whether you’re a researcher, educator, or professional, integrating these Wiris’ technologies into your workflow ensures precision and efficiency.

For instance, to deepen the understanding of e’s behavior, one can visualize the limit expression

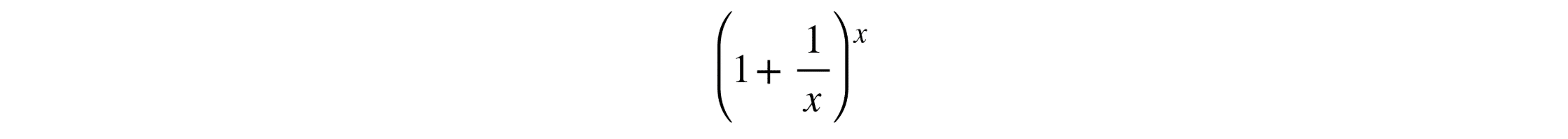
using graphing tools such as CalcMe, a Computer Assisted System (CAS) for algebraic manipulation that allows complex mathematical calculations to be carried over in a self-contained, fast and intuitive way. As increases, the graph approaches the value of number e, offering an intuitive graphical demonstration of this mathematical limit.

Additionally, MathType, the world’s leading equation editor that allows you to write math notation as easily as you write text, enables seamless insertion of complex mathematical expressions into documents and web content, ensuring clarity and precision.

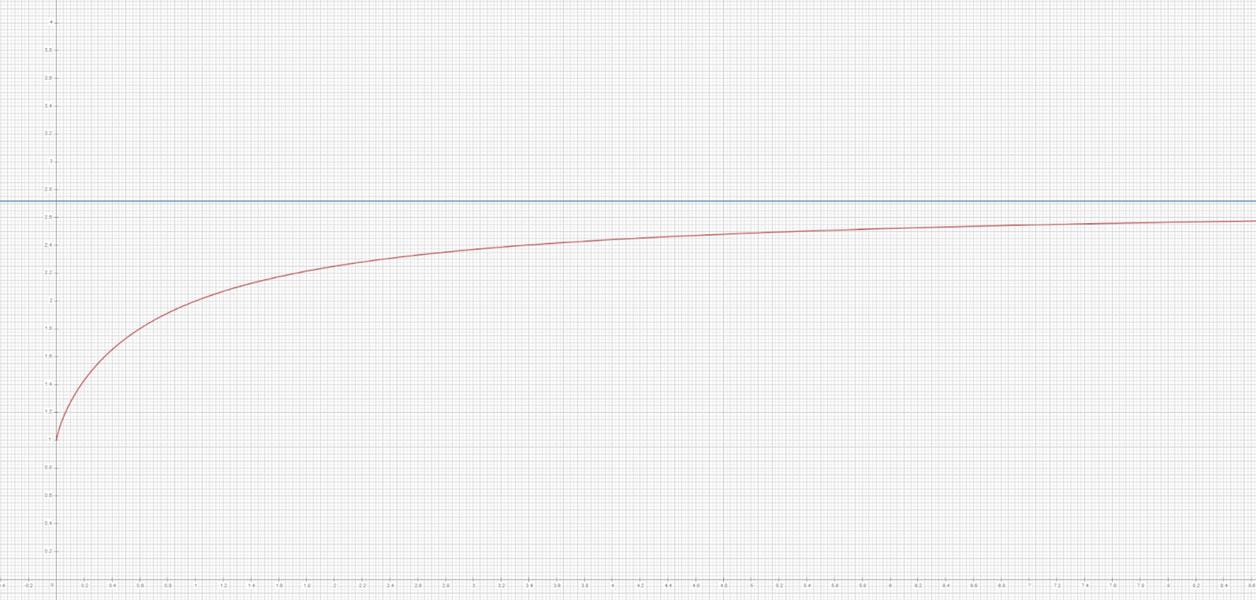
Graph showing the function (1+1/x)^x in red, approaching the value of e in blue.

Perfect for students, teachers, editors, and technical writers, MathType streamlines the creation of high-quality technical and scientific content across various platforms.

For seamless handling of mathematical expressions and visualizations, consider incorporating both MathType and CalcMe into your digital toolkit.

Write your e number equations here!