The Monty Hall Problem Explained Like You’ve Never Seen It 

The Monty Hall problem has puzzled minds for decades, challenging our intuition with a simple question: Should you switch your choice or stay? In this article, we break down the origins, math, and surprising logic of this famous probability puzzle. And we’ll make it all clear using a deck of 52 cards. 

What Is the Monty Hall Problem?

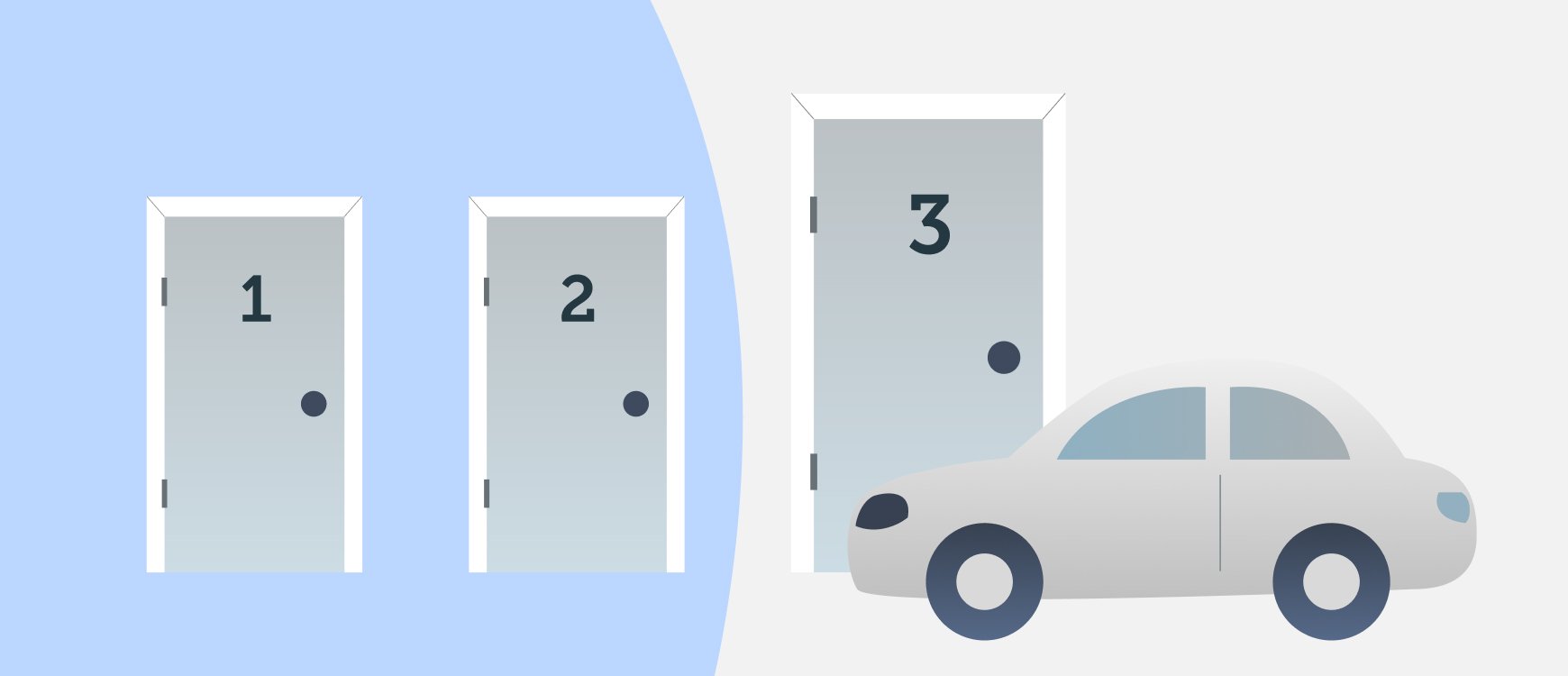
Originally from the TV game show “Let’s Make a Deal,” the Monty Hall Problem presents the following scenario: 

1. You’re shown three doors.  
2. Behind one door is a car (your goal), behind the other two are goats. 
3. You choose a door.
4. The host (Monty Hall), who knows -and that’s very important- what’s behind each door, opens one of the other two doors, revealing a goat.
5. You are then offered a chance to switch your choice to the remaining unopened door.

The question is: Should you switch? Intuition says it doesn’t matter. Math says otherwise. 

At first glance, many people reason that with two unopened doors remaining, the odds must be 50/50 —one door has a car, one has a goat, so switching feels like a coin toss. Others rely on fairness instincts, thinking the host’s intervention somehow resets the probabilities. Some even argue that sticking with their original choice “feels safer” or that the host is trying to trick them. These are all common —and incorrect— intuitive shortcuts that ignore how probability shifts when informed decisions are introduced. The Monty Hall Problem explained exposes how our gut feelings often mislead us in uncertain scenarios.

One of the most famous moments related to this puzzle was when Marilyn vos Savant, known for having the highest recorded IQ, answered a reader’s question about it in Parade magazine. Her correct advice to always switch sparked massive controversy, with thousands of readers —including many math PhDs— insisting she was wrong. Spoiler: she wasn’t.

The Monty Hall Problem Explained is also featured in the movie 21, which helped popularize it among general audiences as a mind-bending probability paradox that highlights how our instincts can fail us in probabilistic scenarios.

The 52-Card Analogy: An Intuitive Breakthrough

To better understand the Monty Hall Problem explained, let’s use a deck of 52 cards to make things clearer:

1. Imagine this: someone puts over the table a full deck of 52 playing cards face down and tells you that the winner is the ace of spades.
2. Now it’s your turn. You choose one random card from all the 52 face down cards, but you still don’t look at it.
3. Then, the host, who knows where the ace of spades is, unveils every card except your card and another one. 
4. At this point, you’re asked: do you want to stick with your original pick or switch to the other remaining card?

Interestingly, while most people tend to stick with their original choice in the classic three-door version of the Monty Hall problem -believing the odds are now even- this behavior often shifts dramatically when the scenario is reframed using 52 cards. Faced with the overwhelming improbability of having picked the right card from the start, most participants instinctively choose to switch. The dramatic contrast in perceived probability makes the logic behind switching much clearer, even for those who struggled with the original dilemma.

Why does the switch make sense? Let’s do some numbers:

• Probability that your first pick is the ace of spades: 1/52 (1,92 %)
• Probability that the card you didn’t choose is the ace of spades: 51/52 (98,08 %) 

The switch clearly becomes the rational choice. This is because your initial pick had only a 1-in-52 chance of being correct, while the remaining unrevealed card now carries the cumulative probability of the other 51 cards, making it far more likely to be the winner. The same logic applies to the original 3-door setup, though with smaller numerical differences: switching still increases your odds from 1/3 to 2/3, illustrating how updated information changes the probability landscape.

FOTO

Cracking the Code: Why Switching in The Monty Hall Problem Makes Mathematical Sense 

Let’s go back to the original situation and simplify the setup so we can get the Monty Hall Problem explained:

• Probability your first choice is the car: 1/3 (33,33 %)
• Probability the car is behind one of the other two doors: 2/3 (66,66 %)

Monty Hall opens a door he knows has a goat -not randomly, but deliberately- to give you more information without revealing the winning door. This action doesn’t change the fact that the initial probability of your first choice being correct remains 1/3. However, since Monty Hall will never reveal the car, the 2/3 probability that the car was in one of the two unchosen doors now shifts entirely to the one unopened door that he didn’t pick. This is why switching increases your odds: Monty Hall’s action narrows the uncertainty without altering the original probabilities. 

To grasp the real advantage of switching, imagine playing the Monty Hall problem 300 times. If you always stick with your initial choice, you would expect to win roughly 100 times, since there’s a one-in-three chance you initially chose the correct door. On the other hand, if you always switch after Monty reveals a goat, you’d win approximately 200 times. This clear difference illustrates how switching leverages the higher probability that the prize was not behind your first choice.

Generalizing the Math: The N-Door Problem

While the classic version of The Monty Hall Problem uses three doors, the underlying logic can be extended to any number of options. By increasing the number of doors, the counterintuitive advantage of switching becomes even more striking. Let’s explore how the probabilities scale when we generalize the problem to n doors.

Let n be the total number of doors (n ≥ 3).

• If you stay, your chance of winning is 1/n.
• If you switch, your chance is (n-1)/n.

To compare these directly, consider the ratio of the two outcomes: [(n-1)/n] divided by [1/n] simplifies to (n-1). This means that switching makes you (n-1) times more likely to win than staying. For example:

• With 3 doors, you are 2 times more likely to win if you switch.
• With 4 doors, you’re 3 times more likely.
• With 10 doors, you’re 9 times more likely.

The number of doors has to be at least three, because with two doors there’s no room for Monty to reveal a goat without ambiguity, and with one door there’s no choice to be made. Hence, the problem only makes logical sense with n ≥ 3.

This variation offers another way to see the Monty Hall Problem explained in action.

Real-World Applications of the Monty Hall Logic

Now that we have The Monty Hall Problem explained, you can see it’s more than just a quirky puzzle. It has real implications in:

• Game theory: The Monty Hall Problem explained illustrates how optimal strategies can emerge in probabilistic games where information is revealed gradually. It highlights the value of updating decisions as new information becomes available, an essential principle in strategic thinking.
• Decision making under uncertainty: In many real-life scenarios, such as financial investments or legal strategies, we face choices with incomplete information. The Monty Hall logic teaches us that re-evaluating decisions when new data surfaces can drastically change outcomes, even when our instincts suggest otherwise.
• Medical diagnostics: Doctors often begin with a set of possible diagnoses and refine their assessments based on test results. Similar to Monty revealing a goat, negative test outcomes help eliminate options, shifting probabilities toward the correct diagnosis and emphasizing the benefit of revising initial assumptions.
• AI and machine learning: Algorithms frequently update their predictions based on feedback and new data, much like how switching improves chances in the Monty Hall setup. The problem underscores the value of adaptive models that refine output as more information is revealed.

Visualize The Monty Hall Problem explained with CalcMe 

Want to explore this visually? Use CalcMe, a dynamic mathematical platform by Wiris, to simulate different values of n and see how the probabilities shift.

CalcMe lets educators and students build interactive math explorations using variables, graphs, and logic-based scripting. It’s perfect for recreating and get the Monty Hall Problem explained and understood.

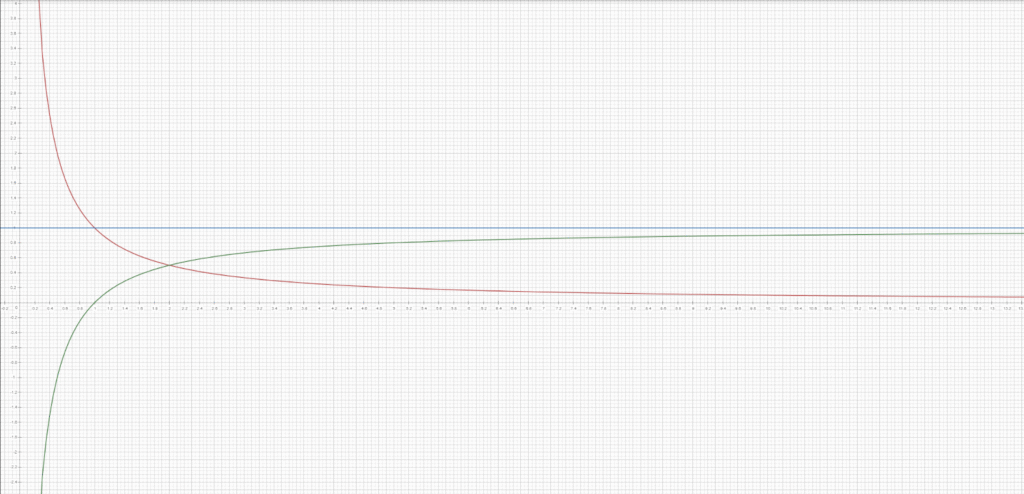
Fig. 1: The green function represents the probability of winning the car if you switch, the red one represents your chances if you don’t switch, and the blue one represents 100%.