Math Olympiad: Solving the First Ever IMO Problem

Mathematical competitions have long challenged students to think creatively and solve problems with elegance and rigor. Among them, the International Math Olympiad stands out as the ultimate stage for young talent. But where did it all begin? Let’s revisit the very first problem ever posed at the IMO and uncover how a timeless algorithm still holds the key to its solution.

1959: The Birth of a Global Math Tradition

The year was 1959. The Cold War was in full swing, and education, especially in the sciences and mathematics, was seen as a strategic priority by many nations. In this context, Romania hosted the first-ever International Mathematical Olympiad, bringing together students from seven countries in Eastern Europe. This marked the beginning of what would become the world’s premier mathematics competition.

Amid the political tensions of the time, this event showcased the power of collaboration and intellectual challenge across borders. The problems selected were designed not only to test knowledge, but also creativity and elegance in mathematical reasoning.

This is the original problem that was proposed in those first Olympiads:

Prove that the fraction is irreducible for every natural number n.

What Is the International Math Olympiad?

The International Math Olympiad (IMO) is one of the most prestigious mathematical competitions in the world. Since its inception in 1959, it has been an annual competition for pre-university students through complex and elegant problems. Hosted by a different country each year, it gathers the most talented young mathematicians globally. Participants face six problems over two days, each requiring deep insight and creative problem-solving.

Over the years, the IMO has become a symbol of excellence in mathematics. Many of today’s renowned mathematicians began their journeys solving Olympiad problems. For students, solving past problems -like the first ever IMO question- is not only intellectually enriching but also great preparation for future contests.

How the Euclidean Algorithm Works (And Why It Matters)

To solve the first IMO problem, we must first understand how to compute the Greatest Common Divisor (GCD) of two numbers. The most efficient way to do this is through the Euclidean Algorithm, a technique dating back to ancient Greece.

Step-by-Step: Euclidean Algorithm in Action

Here’s how it works:

1. Start with two positive integers, say A and B, where A > B.
   
2. Divide A by B, and take the remainder R.
   
3. Replace A with B, and B with R.
   
4. Repeat until the remainder is 0.
   
5. The last non-zero remainder is the GCD.
   

Example:

Let’s find the GCD of 252 and 105:

• 252 ÷ 105 = 2 remainder is 42
  
• 105 ÷ 42 = 2 remainder 21
  
• 42 ÷ 21 = 2 remainder 0
  

So, the GCD of 252 and 105 is the last non-zero remainder: 21.

This algorithm is extremely efficient and works with any pair of integers. You’ll see it in action shortly.

Breaking It Down:

Before diving into the steps, let’s clarify what “mod” means. In mathematics, “mod” stands for modulo, and it refers to the remainder after division. For example, 17 mod 5 = 2 because 17 divided by 5 is 3 with a remainder of 2. It’s a key concept in the Euclidean Algorithm when finding the GCD.

To prove that a fraction is irreducible, we need to show that the numerator and denominator share no common divisors other than 1. In other words, their GCD must be 1.

Let’s denote:

• A = 21n + 4
  
• B = 14n + 3
  

We need to show that GCD(A, B) = 1 for all natural numbers n.

Using the Euclidean Algorithm:

Step 1: Compute A mod B:

(21n + 4) mod (14n + 3)

Step 2: Subtract one time the denominator from the numerator to find the remainder. We compute:
(21n + 4) – 1x (14n + 3) = 21n + 4 – 14n – 3 = 7n + 1

So, the remainder is 7n+1.

Step 3: Next:

(14n + 3) mod (7n + 1)

We compute:

(14n + 3) – 2x (7n + 1) = 14n + 3 – 14n – 2 = 1

So, the remainder is 1.

Step 4: Since the remainder is 1, and 1 is the GCD, the original fraction is irreducible.

Thus, for every natural number n, is indeed irreducible.

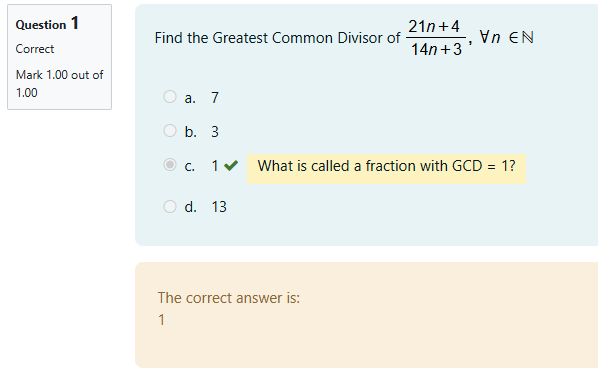
Question generated with WirisQuizzes, one of Wiris’ Assessment tools. 

Why This Math Olympiad Solution Matters

Solving this problem demonstrates how timeless mathematical techniques, like the Euclidean Algorithm, remain incredibly powerful. Even in high-level contests, many solutions rest on foundational principles taught in early algebra classes.

The simplicity of this solution is part of its beauty. It’s a perfect introduction for students tackling their first Math Olympiad problems and an inspiring example of elegant problem-solving.

Real-World Applications of the Euclidean Algorithm

While this example comes from a competition, the Euclidean Algorithm has real-world uses:

• Cryptography: The Euclidean Algorithm is fundamental in RSA encryption, helping generate public and private keys. It’s used to compute modular inverses, essential for encoding and decoding messages securely over the internet. Without it, many cryptographic systems would not function efficiently.
  
• Computer Science: In software engineering, the algorithm helps simplify ratios and optimize code for number-theoretic problems. It’s especially useful in algorithms related to data structures, hashing, and distributed systems where efficiency is crucial.
  
• Engineering: Engineers apply the Euclidean Algorithm in signal processing to simplify frequency ratios and design filters. It helps optimize digital communication systems, ensuring clarity and precision in transmitted signals across networks.

Whether solving a Math Olympiad problem or optimizing computer algorithms, understanding the GCD is immensely useful.

The Importance of Making Math Writing Easier 

The world has changed since 1959. Today, with the rise of digital learning and collaborative education, it’s essential to be able to write mathematical notation clearly and efficiently. Modern educational tools now make this easier than ever, especially when teaching or solving complex problems like those from the Math Olympiad. 

MathType by Wiris simplifies writing math equations digitally, enabling students and educators to create clean, professional-looking notation across platforms such as Google Docs, Microsoft Word, and LMS environments. Whether you’re explaining the Euclidean Algorithm or composing Olympiad-level problems, MathType helps keep the focus on the math, not on formatting.

In addition, Wiris’ Assessment Tools -including WirisQuizzes and LearningLemur– enable educators to design, deliver, and auto-grade math assessments with precision. From step-by-step solutions to dynamic parameters, these tools are ideal for evaluating reasoning processes, much like those used to prove the irreducibility in our IMO problem. They bring the rigor of Olympiad-style problem-solving into the classroom and help track real learning progress.

Conclusion: Math Olympiad Brilliance from Day One

The very first Math Olympiad problem, proposed in 1959, was a brilliant combination of simplicity and depth. By applying the Euclidean Algorithm and understanding the logic behind GCD, we showed that the given fraction is irreducible for any natural number.

This walkthrough not only solves a historical problem but also showcases how foundational tools can tackle sophisticated challenges. Whether you’re preparing for your next competition or just love mathematical puzzles, there’s always something to learn from the past.