Goldbach’s conjecture explained: Origins, proof & math

Why this 18th-century math mystery still fascinates us

Goldbach’s conjecture is one of the oldest and most fascinating unsolved problems in number theory. First proposed in the 18th century, it remains both tantalizingly simple and incredibly difficult to prove. Whether you’re a math teacher, student, or enthusiast, understanding this conjecture opens a window into the elegance of mathematics. In this article, we explore the origins of Goldbach’s conjecture, its implications, and how tools like MathType can help illustrate such complex ideas in the classroom.

The idea is deceptively simple:

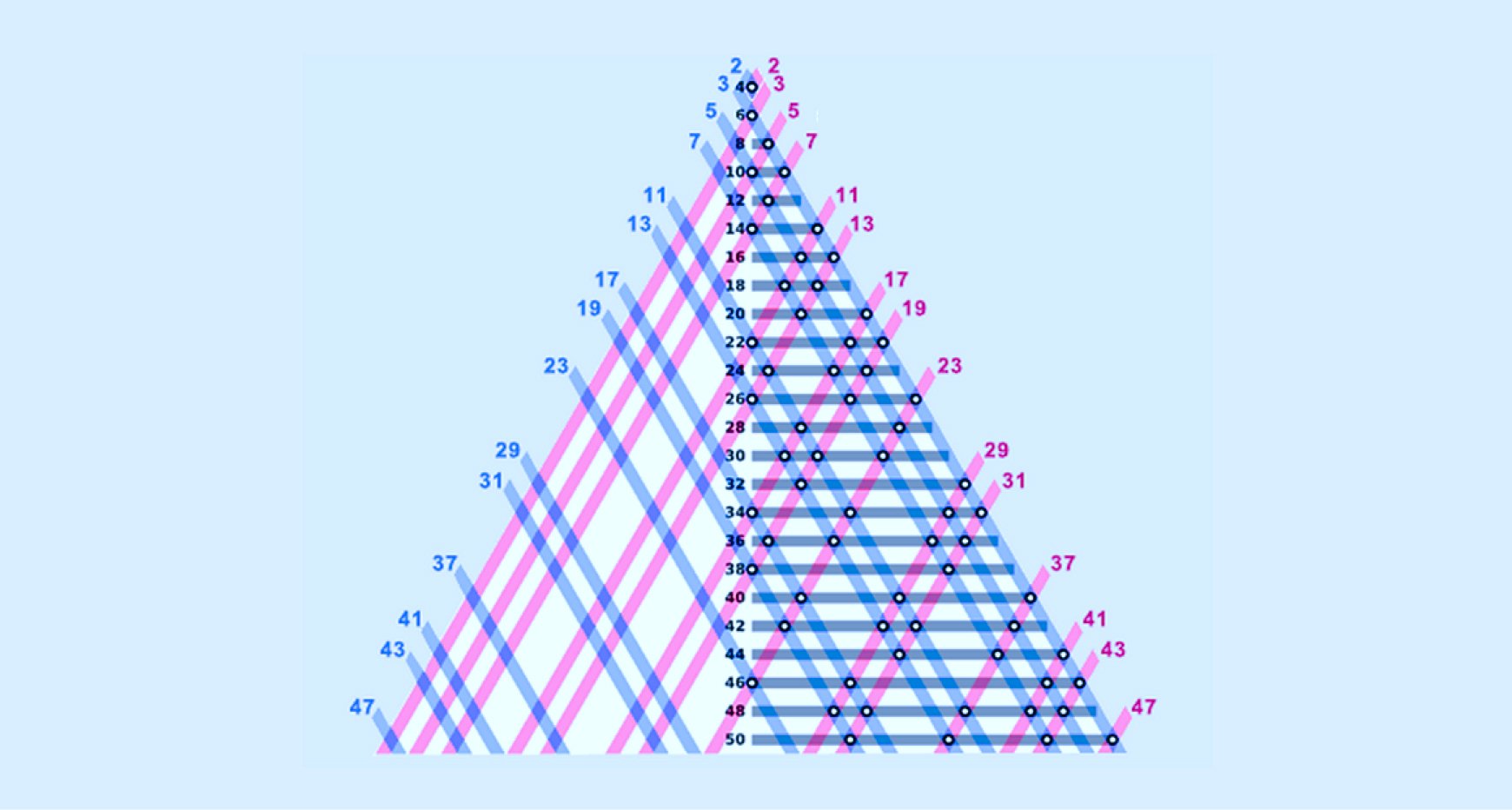
Every even integer greater than 2 can be expressed as the sum of two prime numbers. 

Surprisingly, no one has yet managed to prove that this works for every even number. And yet, despite the lack of a general proof, millions of cases have confirmed its validity. How can something so easy to state be so hard to prove? That’s what makes the Goldbach Conjecture such a beautiful puzzle in mathematics.

What is Goldbach’s conjecture really saying?

Despite being easy to understand, no one has been able to prove this claim for all even numbers. But before we look at why that’s such a big deal, let’s examine what this means in practice.

Origins of the Goldbach conjecture

The conjecture was first proposed by Christian Goldbach in a 1742 letter to the famous mathematician Leonhard Euler. Goldbach originally stated that every number greater than 2 can be written as the sum of three primes (counting 1 as prime). Euler refined what we call the weak Goldbach conjecture into the modern version we know today. Remember that a prime number is a number greater than 1 that has exactly two divisors: 1 and itself.

Figure 1: Original letter from Goldbach to Euler with the proposition of the “weak” conjecture (1742).

Numerical examples

Here are several examples of Goldbach pairs for even numbers:

• 4 = 2 + 2
• 6 = 3 + 3
• 8 = 3 + 5
• 10 = 3 + 7 or 5 + 5
• 12 = 5 + 7
• 14 = 3 + 11 or 7 + 7
• 16 = 3 + 13 or 5 + 11
• 18 = 5 + 13 or 7 + 11
• 20 = 3 + 17 or 7 + 13

These examples help students visualize how primes can pair up in different ways to form the same even number. It also leads to interesting questions: Which even numbers have multiple prime pairings? Do some have only one?

Let’s look at more patterns:

• 28 = 5 + 23, 11 + 17
• 36 = 5 + 31, 7 + 29, 13 + 23, 17 + 19
• 50 = 3 + 47, 7 + 43, 13 + 37, 19 + 31, 23 + 27 (invalid), 29 + 21 (invalid)

This also shows that not every sum of two odd numbers results in valid primes. Students must check that both numbers in the pair are prime.

Can it be proven? Attempts to crack the conjecture

Although no one has definitively proven Goldbach’s conjecture, many mathematicians have tried, often using advanced number theory, heuristic arguments, or computer-based checks.

The conjecture has become a benchmark challenge: simple to state, yet hiding layers of mathematical complexity. Every effort to prove it pushes the boundaries of our understanding of prime distribution. The search for a Goldbach conjecture proof remains one of the most compelling pursuits in modern mathematics.

Computational verification

Using modern computing power, the conjecture has been verified for all even integers up to 4 × 10¹⁸. That’s 4 quintillion. This means that for all even numbers within that range, at least one pair of prime numbers has been found that sums to it. This massive computational effort involved clever algorithms, prime sieving techniques, and distributed computing networks.

But here’s the catch: computational verification, no matter how extensive, doesn’t equal a proof. It only confirms that the conjecture holds for all cases tested. Mathematically speaking, there could still be a counterexample beyond that range.

Theoretical advances

Several significant partial results have emerged:

• Vinogradov’s Theorem (1937): Proved that every sufficiently large odd number can be written as the sum of three primes. Though not directly the same, it supports the spirit of Goldbach’s idea.
• Deshouillers, Effinger, Granville, and te Riele (1997): Under the Generalized Riemann Hypothesis, they proved Goldbach’s conjecture holds for all even numbers greater than 4.
• Helfgott’s Proof (2013): Harald Helfgott finally proved the weak Goldbach conjecture (that every odd number greater than 5 is the sum of three primes).

These breakthroughs are milestones, but they still leave the “strong” version –every even number greater than 2 is the sum of two primes– unproven. The mathematical community continues to search for a complete and unconditional Goldbach conjecture proof.

Why has no one proven it yet?

The problem lies in the nature of prime numbers themselves. Primes are the building blocks of all integers, but their distribution is irregular. As numbers get larger, primes become less frequent and more unpredictably spaced.

For example:

• Between 10 and 20, we find four primes: 11, 13, 17, 19.
• But between 90 and 100, there are only two: 97 and 89.

This uneven distribution complicates the task of generalizing a rule for every even number. Consider the even number 100:

• 100 = 3 + 97
• 100 = 11 + 89
• 100 = 17 + 83
• 100 = 29 + 71
• 100 = 41 + 59
• 100 = 47 + 53

While many pairings exist, there’s no known formula that guarantees such combinations for every even integer.

To prove Goldbach’s conjecture, one would need a universal method to show that, for any even number, such a pair of primes always exists. But no such method currently exists that accounts for the randomness in how primes appear.

Furthermore, the problem is not just about addition: it connects deeply with analytic number theory and the behavior of the Riemann zeta function, making it a challenging and multidimensional puzzle.

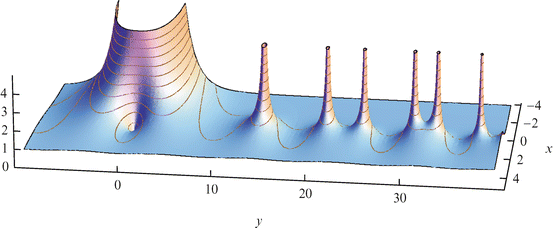
Figure 2: 3D plot of the Riemann zeta function

Mathematically, even expressing the density of primes that sum to a given even number involves advanced tools like circle methods and sieve theory, which themselves depend on assumptions still being researched.

Prime Numbers Aren’t Just Theory: Real Applications

Understanding prime numbers isn’t just a theoretical pursuit. Prime numbers are fundamental in:

• Cryptography: Secure communication relies on the difficulty of factoring large primes.
• Computer science: Algorithms often use primes for hashing and random number generation.
• Data compression and error detection: Prime-based methods support reliable data transmission.

The relevance of prime numbers adds weight to why conjectures like Goldbach’s matter.

Explore, Visualize, and Teach Goldbach’s Conjecture with Confidence

Here are a few ways to explore the Goldbach conjecture interactively:

• Pick any even number and find all its Goldbach pairs.
• Use MathType to create a chart of even numbers up to 100 with all valid prime pairings.
• Analyze which primes appear most often in the pairings.

This hands-on approach fosters critical thinking and mathematical creativity.

Bring It to Life with MathType

MathType by Wiris is an equation editor that allows you to write and present mathematical expressions clearly.

With MathType, educators can:

• Create exercises to explore Goldbach pairs for various even numbers.
• Present prime number decompositions visually.
• Create interactive assignments where students search for prime pairs using patterns and logical deduction.

MathType integrates with LMS platforms, supports LaTeX, and simplifies equation editing in both web and desktop formats: ideal for classroom use.

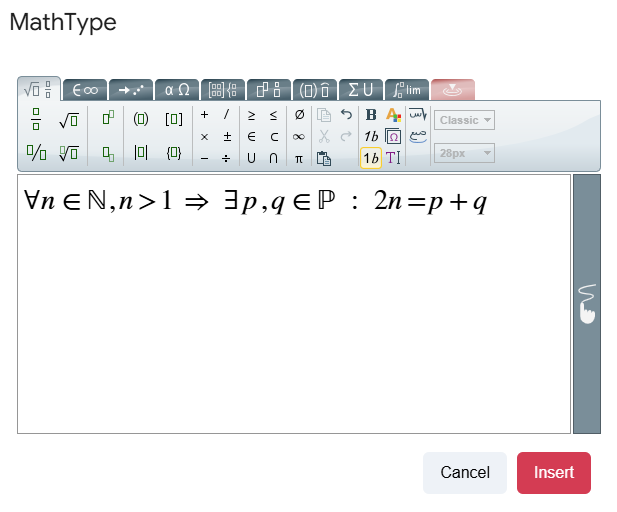
Figure 3: The Goldbach’s conjecture written with MathType

Want to Explore Math Deeper?

Goldbach’s conjecture shows how deep questions can arise from simple ideas. Tools like MathType empower educators and students to delve into these ideas with clarity and precision.

Try MathType to bring mathematical expressions to life in your lessons or projects.