Descubre un ejemplo de resolución de un sistema de ecuaciones y aprende a generar variables aleatorias con Wiris para crear ejercicios ilimitados.
Aprender matemáticas requiere más que solo entender teorías: la clave para dominar conceptos complejos y perfeccionar habilidades está en la práctica continua. Sin embargo, los métodos tradicionales a menudo limitan el proceso de aprendizaje: una vez que el estudiante ha resuelto un problema, el desafío desaparece, y los exámenes suelen repetir las mismas preguntas, perdiendo así su valor como herramienta de evaluación. Imagina tener la posibilidad de generar ejercicios ilimitados con variables aleatorias, adaptados a las necesidades de cada estudiante. Con Wiris, esto ya es posible.
Además, cuenta con corrección automática, lo que significa que, mientras se genera el ejercicio, se calcula la respuesta de forma simultánea. Esto permite recibir retroalimentación al instante, facilitando el aprendizaje y la corrección de errores de manera inmediata.
Para los profesores, esta herramienta ofrece una ventaja clave: la posibilidad de generar una cantidad infinita de ejercicios, cada uno único. De este modo, los docentes pueden crear experiencias de aprendizaje variadas y personalizadas, garantizando que los alumnos enfrenten nuevos retos en cada práctica.
Por su parte, los estudiantes disfrutan de una práctica constante que les permite reforzar sus habilidades sin la preocupación de repetir los mismos ejercicios. Además, esta capacidad de generar ejercicios ilimitados les ofrece una excelente preparación para los exámenes.
Ejemplo práctico: Resolución de un sistema de ecuaciones lineales
Para ilustrar cómo funciona esta herramienta y cómo puede ser utilizada en el aula, vamos a centrarnos en la resolución de sistemas de ecuaciones lineales. Elegimos este tipo de problemas porque representan un reto matemático común al que se enfrentan todos los estudiantes y ofrecen la posibilidad de explorar diferentes métodos de resolución. Además, los sistemas de ecuaciones pueden tener diversas características, como ser compatibles, incompatibles o indeterminados, permitiendo a los estudiantes trabajar con una amplia gama de situaciones.
Imaginemos que tenemos el siguiente sistema de ecuaciones lineales de tres incógnitas: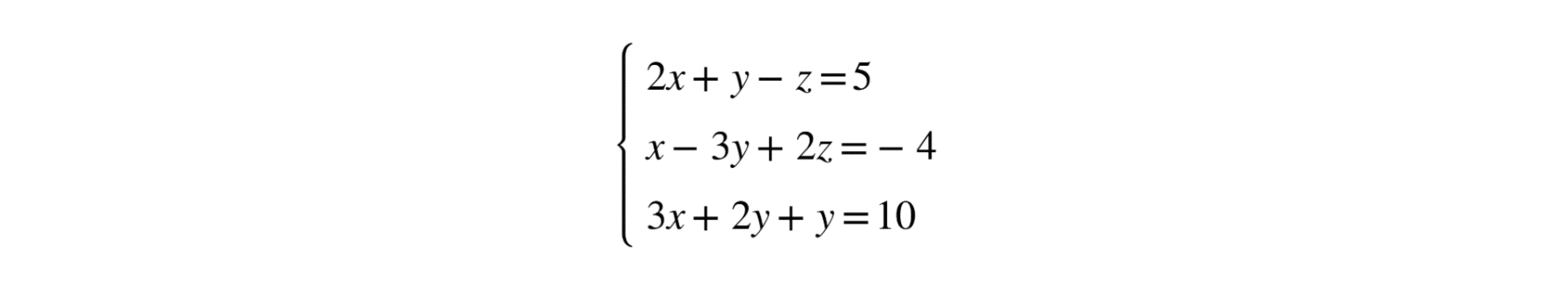
Vamos a resolverlo utilizando el Método de Gauss. El primer paso es escribir el sistema en forma de matriz aumentada:
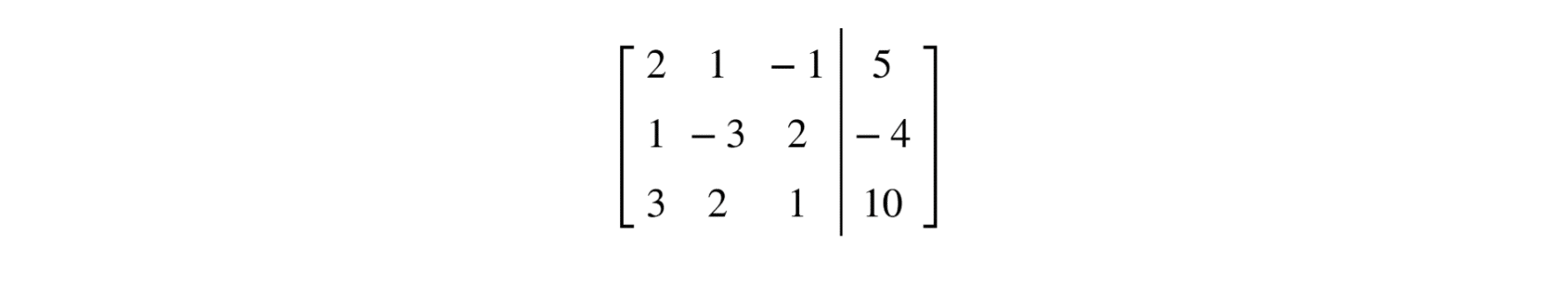
Ahora vamos a aplicar operaciones elementales para reducir la matriz a su forma escalonada.
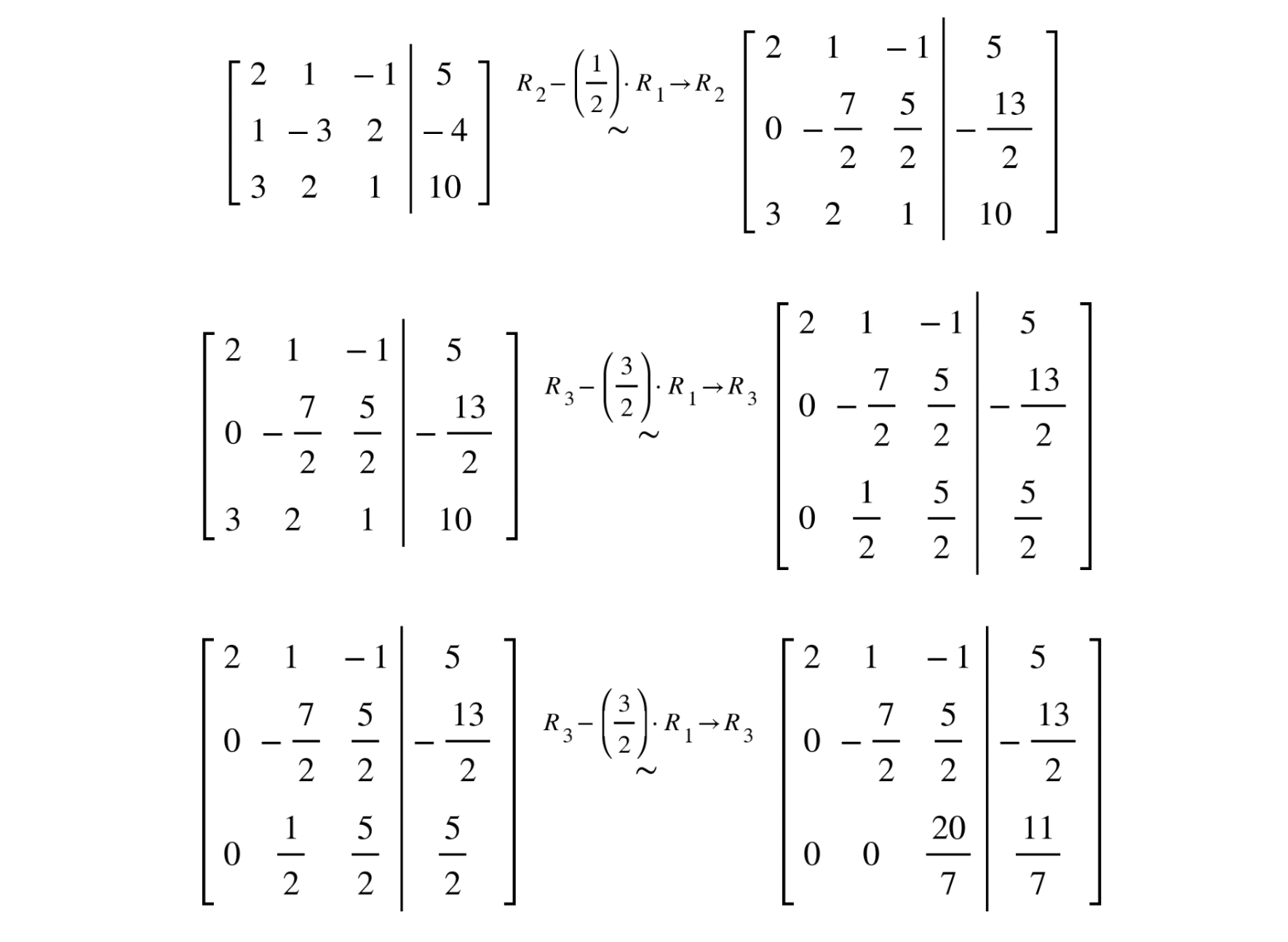
Por lo que obtenemos:
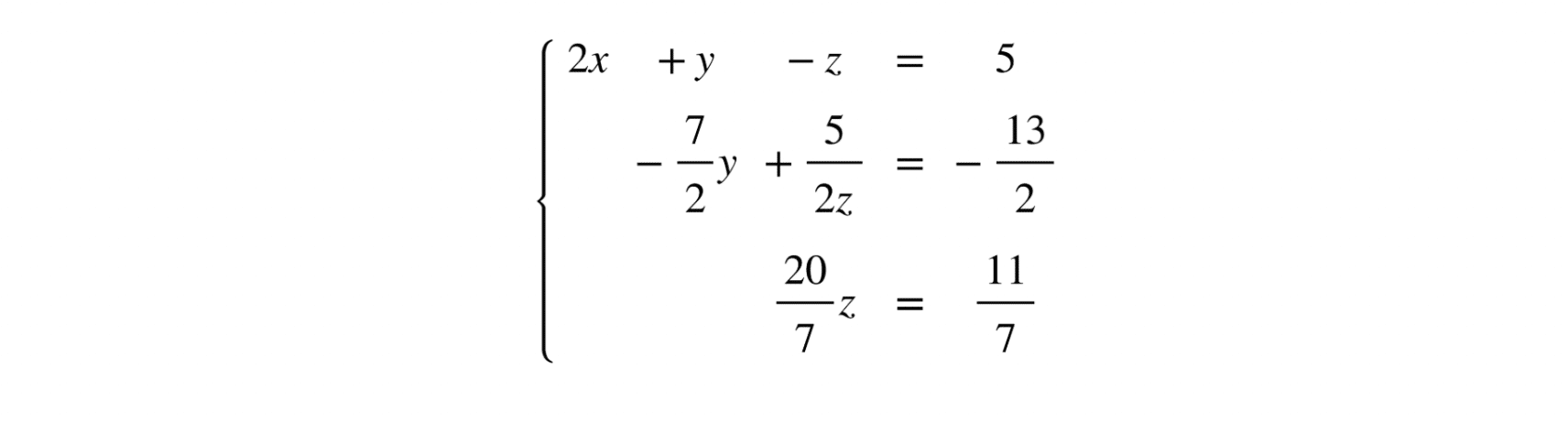
A partir de la ecuación 3 del sistema, encontramos la variable :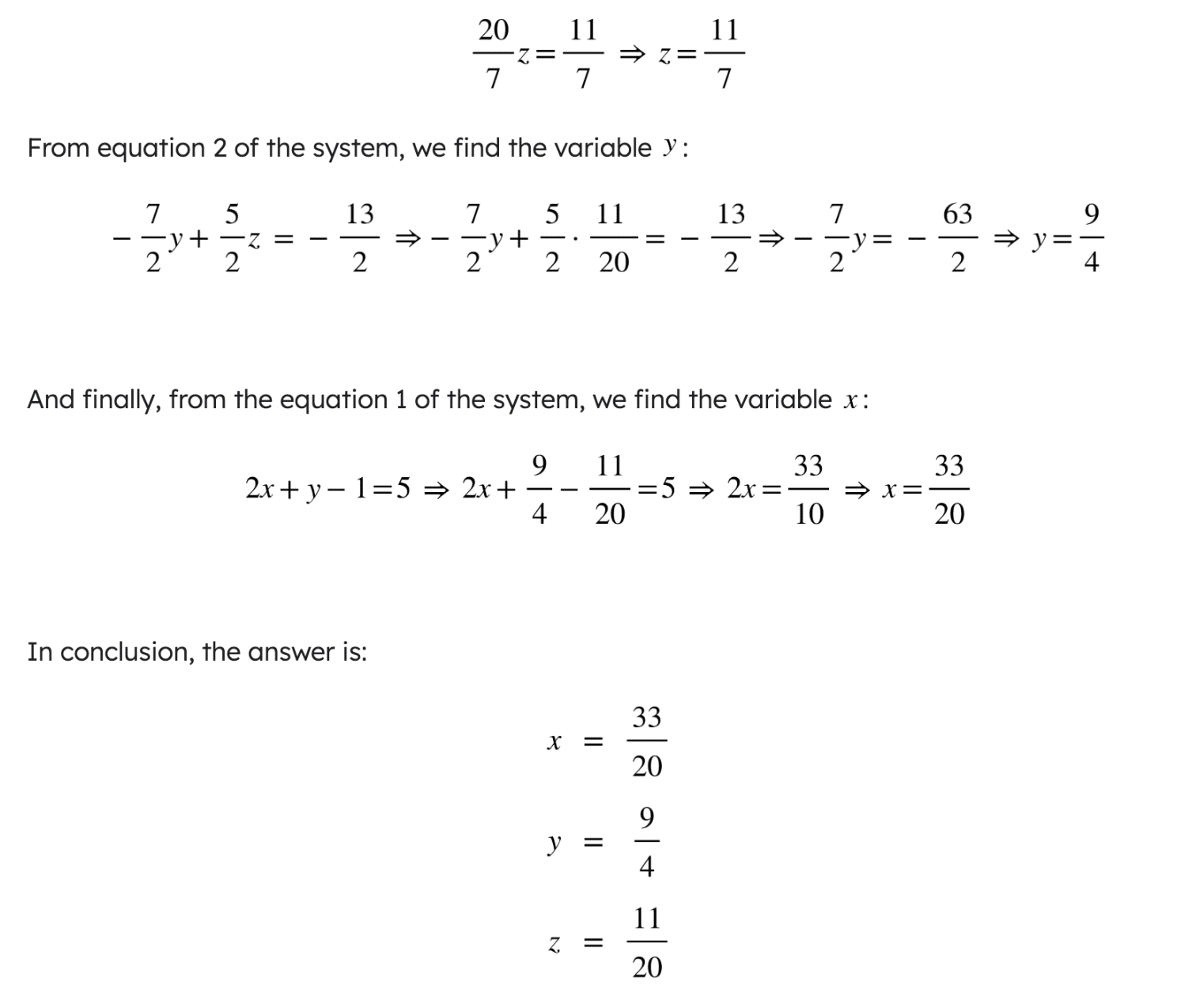
Generación ilimitada de sistemas de ecuaciones lineales con
variables aleatorias
Ahora que hemos resuelto este sistema, para seguir practicando, nos gustaría poder generar nuevos sistemas de ecuaciones de la misma forma, pero con valores aleatorios.
Estos sistemas tendrían la forma siguiente:
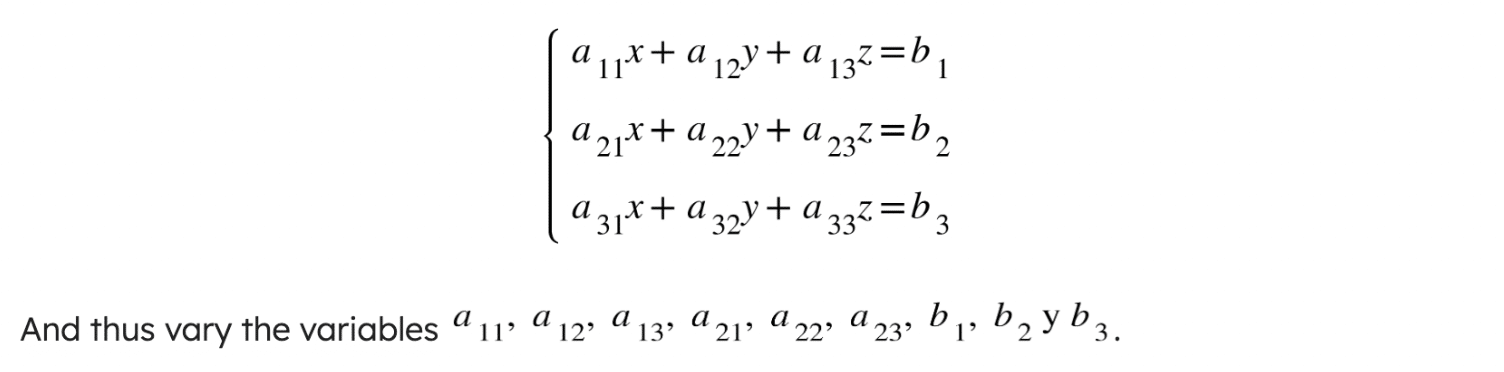
A continuación, te mostramos un ejemplo de código para implementar esta funcionalidad y generar sistemas de ecuaciones aleatorios determinados. ¡Con Wiris, es totalmente posible!
r() := random(-4,4)
sol = [r() with i in 1..3]
[a,b,c] = sol
repeat
A = [[r() with i in 1..3] with j in 1..3]
until determinant (A) != 0
b = A * sol
ec = {}
for i in 1..3 do
ecaux = A.i * [x,y,z]
ec = append(ec, ecaux = b.i)
end
{ec1, ec2, ec3} = ec
r() := random(-4,4): Esta función genera un número aleatorio entre -4 y 4.
sol = [r() with i in 1..3]: Aquí, se generan tres valores aleatorios que representarán las soluciones del sistema de ecuaciones.
[a,b,c] = sol: Los valores generados se asignan a las incógnitas del sistema.
repeat…until determinant(A) != 0: Este bloque asegura que la matriz de coeficientes A sea invertible (es decir, que su determinante no sea cero), lo que garantiza que el sistema tiene una solución única.
b = A * sol: Se calcula el vector de resultados b multiplicando la matriz de coeficientes A por las soluciones sol.
for i in 1..3 do: En este ciclo se generan las tres ecuaciones, usando cada una de las filas de la matriz A y las soluciones sol.
{ec1, ec2, ec3} = ec: Finalmente, las tres ecuaciones generadas se almacenan en las variables ec1, ec2 y ec3, listos para ser utilizados en nuevos ejercicios.
Utilizando WirisQuizzes e implementando este código como pregunta, podemos obtener los siguientes resultados:
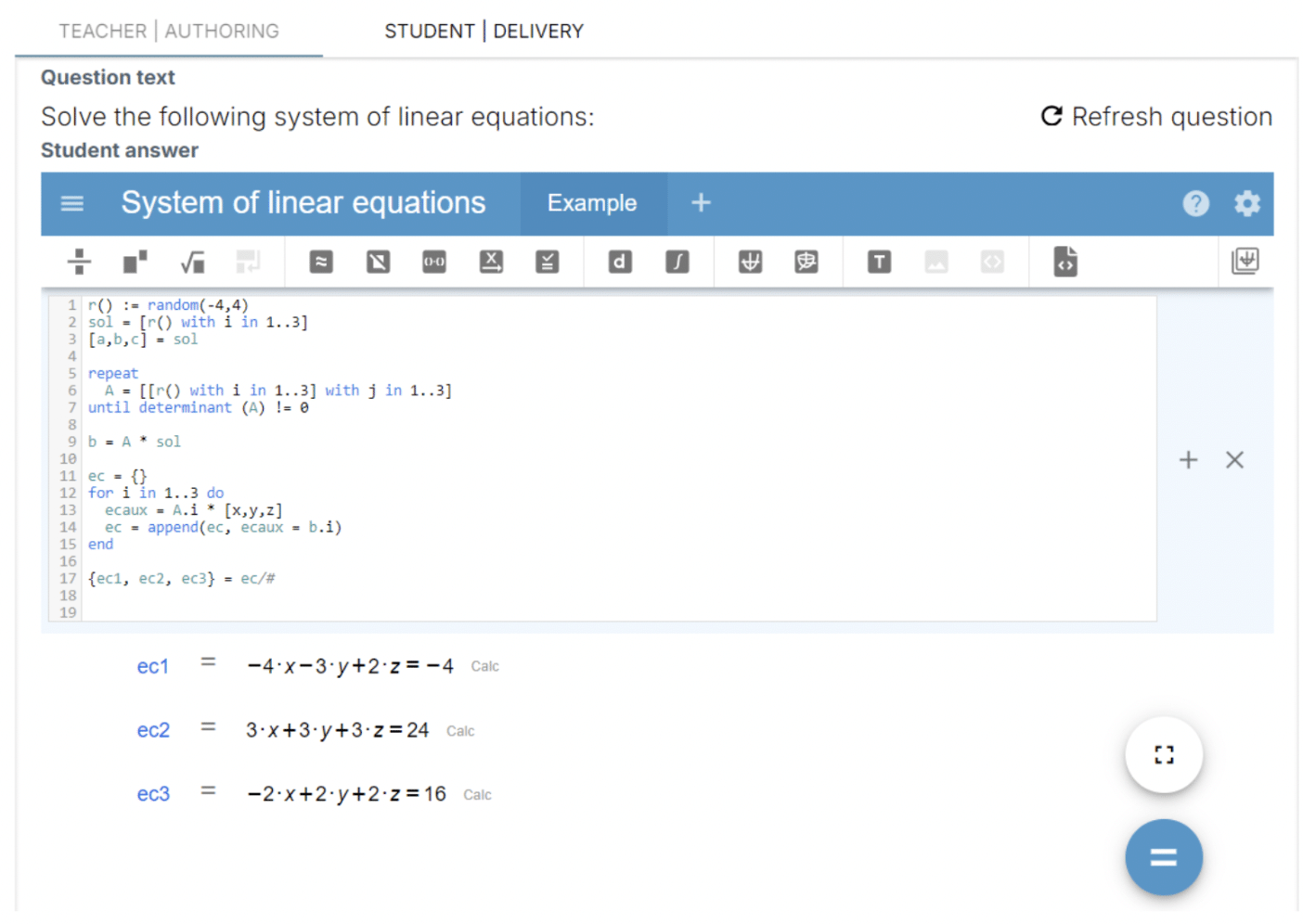
Al recargar otro sistema con el símbolo «=» se genera un nuevo conjunto de ecuaciones, como se muestra a continuación:
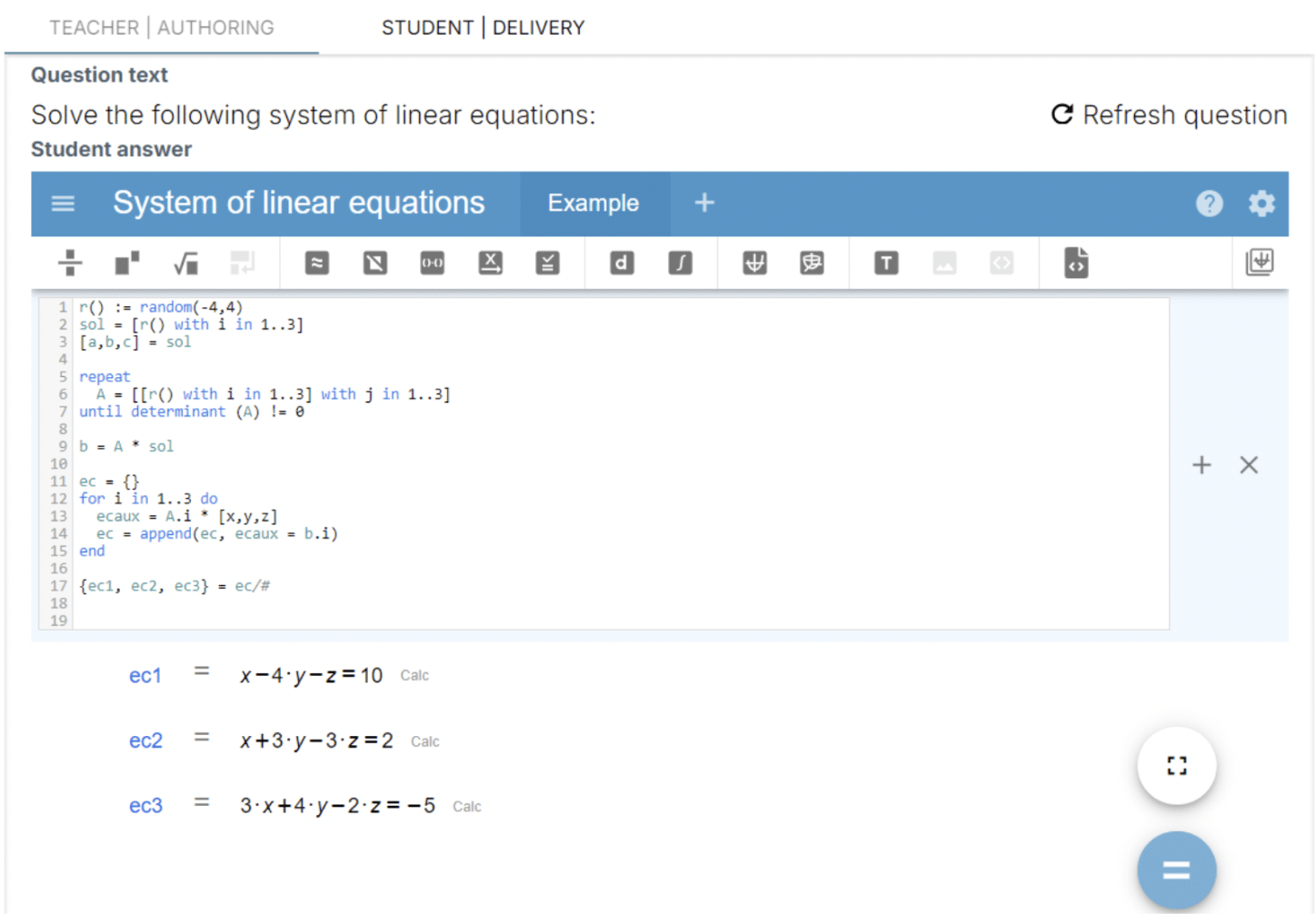
Para obtener más detalles, puedes consultar toda la documentación del producto aquí.
Si te ha sido útil, te invitamos a compartirlo con otros compañeros, compañeras, profesores o alumnos. Además, estaremos encantados de conocer tu opinión y cualquier sugerencia que puedas tener.
