Explora la paradoja del cumpleaños. Calcula la probabilidad de que dos personas compartan la misma fecha, con ejemplos y gráficos explicativos.
La fascinante probabilidad de compartir fecha
La paradoja del cumpleaños es uno de esos conceptos matemáticos que nos invitan a desafiar nuestra intuición. Una paradoja, en esencia, es una afirmación o resultado que, aunque aparentemente contradictorio o contrario a la lógica común, se demuestra como cierto cuando se analiza detenidamente. En el caso de la paradoja del cumpleaños, el escenario es simple pero desconcertante: ¿cuántas personas deben estar en una sala para que la probabilidad de que al menos dos compartan el mismo cumpleaños sea mayor al 50%?
El resultado será sorprendentemente bajo, pero ¿te atreves a contestar antes de seguir leyendo y revelar la respuesta?
Lo más intuitivo sería pensar que se necesitan al menos 183 personas, la mitad de los días del año, para que la probabilidad de que dos personas compartan el mismo cumpleaños sea mayor al 50%. Sin embargo, la realidad es muy diferente.
Para entender cómo se calcula esta probabilidad, recordemos que la fórmula básica de cualquier probabilidad consiste en dividir los casos favorables entre los casos totales.
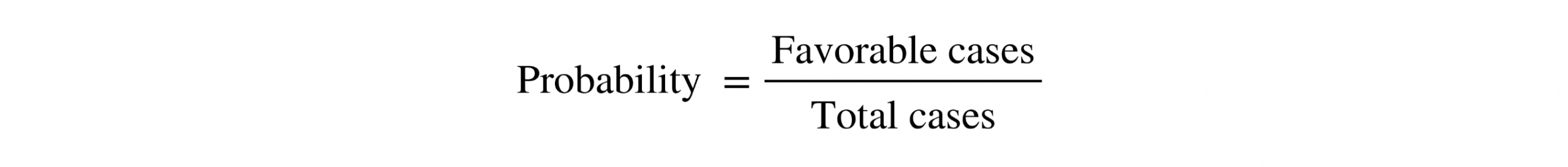
En este caso, en lugar de calcular directamente la probabilidad de coincidencia, es más sencillo comenzar calculando la probabilidad de que ninguna persona comparta cumpleaños con otra. Una vez que tenemos esta probabilidad, podemos restarla a 1 para obtener la probabilidad de coincidencia.
Para calcular la probabilidad de que ninguna persona comparta cumpleaños con otra, procederemos de forma constructiva, evaluando escenario por escenario.
- Si en una sala solo hay una persona, no existe la posibilidad de que comparta su cumpleaños con alguien más, ya que no hay otras personas presentes. Por lo tanto, la probabilidad de que su cumpleaños sea único es del 100%, es decir 365/365.
- Ahora, si entra una segunda persona, la probabilidad de que su cumpleaños sea diferente al de la primera es 364/365, ya que solo hay 364 días restantes en los que puede nacer para evitar una coincidencia.
- Si se agrega una tercera persona, la probabilidad de que su cumpleaños no coincida con los de las dos primeras personas es 363/365, ya que ahora hay dos días ocupados.
Por lo tanto, para n personas, se deben cumplir todas las condiciones anteriores de forma simultánea: que la segunda persona no comparta cumpleaños con la primera, que la tercera no comparta con las dos anteriores, y así sucesivamente. Esto implica que la probabilidad de que ninguna de las n personas comparta el mismo cumpleaños es el producto de las probabilidades individuales:
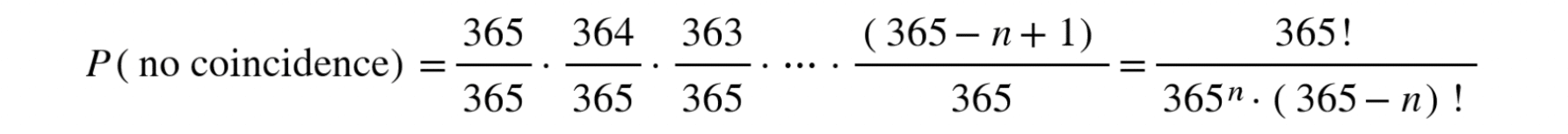
Y finalmente obtenemos:
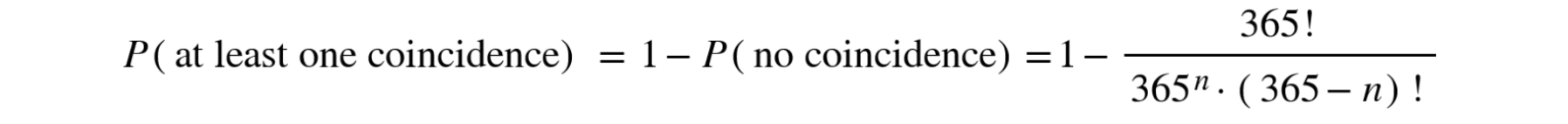
Analizando probabilidades para distintos valores de n
Examinemos los resultados para diferentes valores de n:
- Para n=10 obtenemos que P (almenos una coincidencia) = 11,61%
This calculation has been created using CalcMe
- Para n=15 obtenemos que P (almenos una coincidencia) = 25,03%
- Para n=23 obtenemos que P (almenos una coincidencia) = 50,05%
- Para n=50 obtenemos que P (almenos una coincidencia) = 96,53%
- Para n=60 obtenemos que P (almenos una coincidencia) = 99,22%
Como podemos observar en los ejemplos anteriores, para alcanzar una probabilidad superior al 50%, solo se necesitan 23 personas en una misma sala. Este resultado puede parecer sorprendente, pero tiene sentido si consideramos que con 23 personas se pueden formar 253 pares diferentes, y cada uno de estos pares representa una oportunidad para que dos personas compartan el mismo cumpleaños. Aún más sorprendente es que para tener una probabilidad superior al 99%, sólo se necesitan 60 personas, lo que demuestra cómo el número de combinaciones posibles crece rápidamente con cada nueva persona añadida.
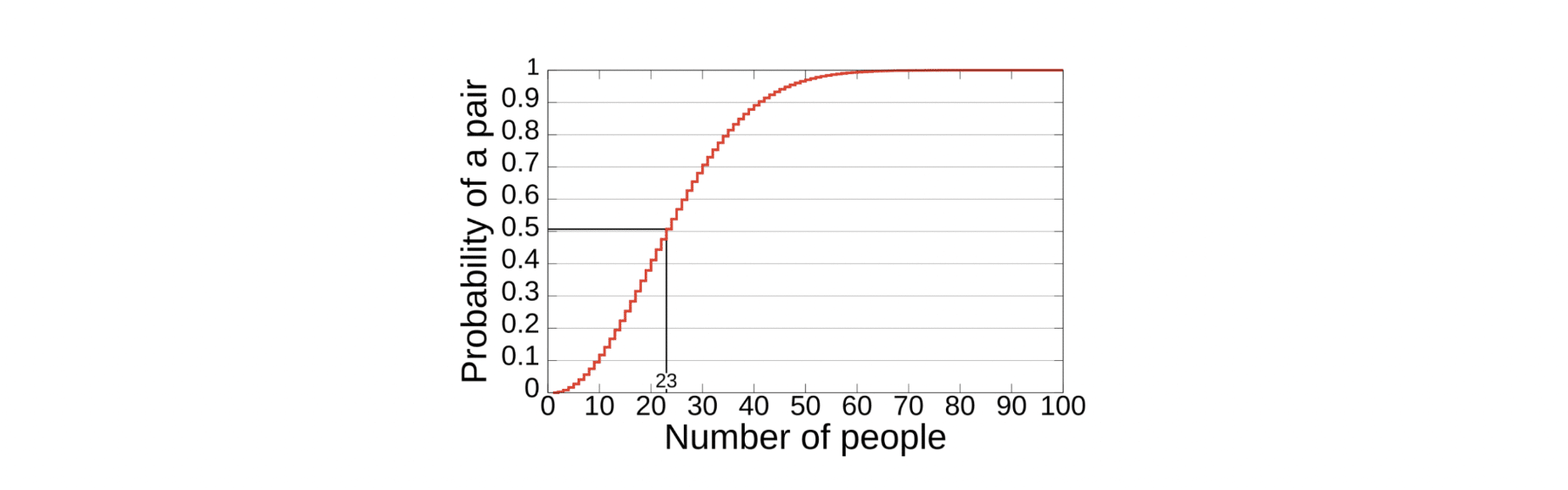
Esta es la gráfica de la distribución de probabilidad:
Gráfico que muestra la probabilidad de que dos personas compartan cumpleaños, con el número de personas en el eje X y la probabilidad en el eje Y, expresada en porcentaje.
En contraste, si en lugar de calcular la probabilidad de coincidencia entre cualquier par de personas consideramos la probabilidad de que alguien en una sala de n personas (excluyéndote a ti) comparta específicamente tu cumpleaños, el cálculo es diferente. Esta probabilidad está dada por:
P(alguien con el mismo cumpleaños que tu) =1-(364/365)
Para n=22, esta probabilidad es de aproximadamente 0.059 (5.9%), lo cual es bastante baja. De hecho, sería necesario que hubiera al menos 253 personas en la sala para que esta probabilidad supere el 50%.
La paradoja del cumpleaños es un recordatorio fascinante de cómo nuestra intuición puede fallar frente a la lógica matemática.
Ahora que conoces la paradoja del cumpleaños y sus conceptos clave, ¿puedes calcular la probabilidad de que exactamente k personas dentro de un grupo de n personas compartan su cumpleaños? ¡Nos encantaría conocer tus resultados en los comentarios del blog! Si el artículo te ha sorprendido, compártelo con tus amigos para que también descubran esta curiosidad matemática. Además, si te interesa probar estos cálculos por ti mismo, echa un vistazo a CalcMe.
