Cuando se habla de constantes matemáticas fundamentales, π suele acaparar la atención. Sin embargo, hay otro número, igualmente vital aunque menos celebrado: el número e de Euler. Conocido simplemente como e, esta constante aparece en innumerables contextos matemáticos y aplicaciones prácticas. En este artículo exploraremos el origen, las propiedades y las aplicaciones de e, posicionándolo como una herramienta indispensable en el mundo de las matemáticas, la ciencia y las finanzas.
¿Qué es el número e de Euler?
El número e de Euler es un número irracional y trascendental, aproximadamente igual a 2.71828. Sirve como base de los logaritmos naturales y surge de manera natural en diversos procesos de crecimiento y en cálculos de límites.
El origen de e: un ejemplo práctico
Consideremos el siguiente escenario real: imagina un banco que ofrece una tasa de interés anual del 100% sobre una inversión principal de 1 €. Si el interés se capitaliza una vez al final del año, tendrás 2 €. Sin embargo, si el banco capitaliza intereses semestralmente al 50% cada seis meses, el cálculo cambia:
- Tras seis meses: 1€ × 1.5 = 1.5€
- Tras otros seis meses: 1.5€ × 1.5 = 2.25€
Ahora, dividamos el año en tres periodos de cuatro meses cada uno, aplicando una tasa del 33.33% cada cuatro meses:
- Tras cuatro meses: 1€ × 1.33 = 1.3333€
- Tras ocho meses: 1.3333€ × 1.3333 ≈ 1.7777€
- Tras doce meses: 1.7777€ × 1.3333 ≈ 2.3703€
Entonces, si recibes pagos infinitos, ¿tendrás dinero infinito? Lamentablemente, la respuesta es no. A medida que la frecuencia aumenta —de trimestral a mensual, diaria y más allá— el monto final se aproxima a un límite. La fórmula para calcularlo es:
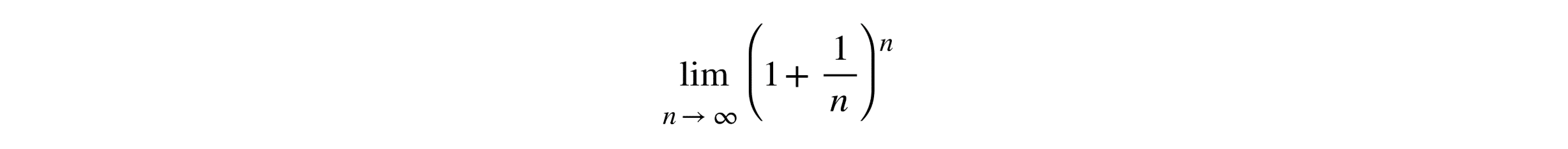 Imagen creada com MathType
Imagen creada com MathType
Cuando n tiende a infinito, el valor converge a e. Este ejemplo simple pero poderoso demuestra la aparición natural de e en el crecimiento exponencial, explicando su papel fundamental en los modelos de interés compuesto continuo.
Propiedades fundamentales del número e
- Irracionalidad: e no puede expresarse como una fracción simple.
- Trascendencia: e no es raíz de ningún polinomio no nulo con coeficientes racionales.
- Serie infinita: e puede representarse como la suma de la serie infinita.
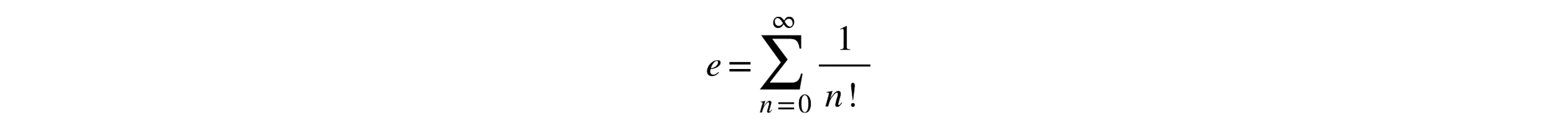
Image created with Wiris’ MathType
- Base del logaritmo natural: la función logaritmo natural utiliza e como base, siendo integral en el cálculo y en modelos de crecimiento natural.
- Identidad de Euler: considerada una de las ecuaciones más bellas de las matemáticas:
eiπ + 1 = 0
Esta ecuación conecta elegantemente cinco constantes fundamentales: 0, 1, e, i, y π.
Aplicaciones en distintas disciplinas
El número e de Euler no es solo una constante fundamental en matemáticas puras, también desempeña un papel central en múltiples aplicaciones prácticas en diversos campos científicos y tecnológicos. Desde modelar procesos de crecimiento hasta la gestión de riesgos, e es indispensable para comprender y predecir fenómenos complejos.
En Matemáticas
- Cálculo: el número e es central en el cálculo, particularmente en el contexto del crecimiento y el decaimiento exponencial. Una de las propiedades más importantes de e es que la derivada de la función ex es ex en sí misma. Esta propiedad única lo hace extremadamente útil en la resolución de ecuaciones diferenciales que describen sistemas dinámicos, como el crecimiento poblacional, la desintegración radiactiva y la transferencia de calor. Simplifica el análisis de estos sistemas porque la función se replica bajo diferenciación.
- Números complejos: la fórmula de Euler, eix = cos(x) + isin(x), es una de las ecuaciones más profundas de las matemáticas, vinculando las funciones exponenciales con las trigonométricas. Esta relación es crucial en campos como la ingeniería eléctrica y el procesamiento de señales, donde simplifica el análisis de sistemas y ondas oscilantes. Permite una comprensión más intuitiva de rotaciones y oscilaciones en el plano complejo.
En Física
- Desintegración radiactiva: el proceso de desintegración radiactiva sigue una ley exponencial, que puede modelarse usando e. La cantidad de sustancia radiactiva restante después de un periodo se da mediante la ecuación N(t) = N0eλt, donde N(t) es la cantidad en el tiempo t, N0 la cantidad inicial y λ la constante de desintegración. Este modelo se utiliza en medicina (radiología), arqueología (datación por carbono) y física nuclear.
- Termodinámica: en termodinámica, el factor de Boltzmann es esencial para determinar la probabilidad de que un sistema esté en un estado de energía particular. La relación exponencial que incluye e es vital para comprender sistemas en equilibrio, como la distribución de partículas en gases o el comportamiento de moléculas en procesos biológicos.
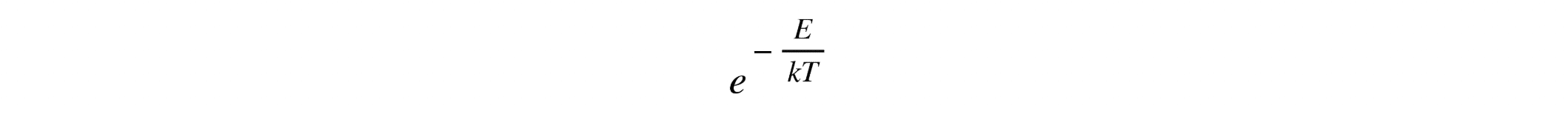
En Economía y Finanzas
- Interés compuesto continuo: uno de los usos más comunes de e es en el cálculo del interés compuesto continuo. Si los intereses se capitalizan continuamente, la fórmula para el valor acumulado es A = Pert, donde P es la inversión inicial, r la tasa de interés y t el tiempo en años. Esto es fundamental para entender el crecimiento a largo plazo de inversiones y ahorros.
- Modelos de riesgo: modelos financieros como Black-Scholes para la valoración de opciones dependen en gran medida de e para representar la naturaleza estocástica de los precios de los activos. e también juega un papel clave en modelos de riesgo como el cálculo de Value at Risk (VaR), que ayuda a cuantificar la probabilidad de pérdidas extremas en carteras de inversión.
En Tecnología
- Algoritmos: e se utiliza en análisis algorítmico, particularmente al analizar el rendimiento de algoritmos que muestran crecimiento exponencial. Procesos aleatorios y algoritmos como QuickSort implican e en sus tiempos de ejecución esperados.
- Aprendizaje automático y ciencia de datos: en machine learning, e aparece en algoritmos que modelan procesos de crecimiento o en algoritmos de optimización que ajustan parámetros con decaimiento exponencial. Por ejemplo, en el descenso de gradiente, las tasas de aprendizaje pueden decrecer exponencialmente basadas en e para optimizar el rendimiento.
En Biología y Medicina
- Crecimiento poblacional: uno de los usos más conocidos de e es en el modelado del crecimiento poblacional. En condiciones ideales, la población sigue una curva exponencial, que se modela mediante la ecuación P(t) = P0ert, donde 𝑃(𝑡) es la población en el momento 𝑡, P0 es la población inicial y 𝑟 es la tasa de crecimiento. Este principio también es relevante en epidemiología paraentender la propagación de enfermedades.
- Farmacocinética: el modelo de decaimiento exponencial también se usa e farmacocinética, que estudia cómo los fármacos se absorben, distribuyen, metabolizan y eliminan. La concentración de un medicamento en sangre a lo largo del tiempo suele seguir una curva de decaimiento exponencial, gobernada por e. Esto ayuda a determinar pautas de dosificación que aseguren niveles terapéuticos sin toxicidad.
Visualizando el número e con herramientas digitales de Wiris
A medida que avanzan las soluciones digitales, herramientas como MathType y CalcMe permiten trabajar fácilmente con e y otras expresiones matemáticas complejas. Ya seas investigador, docente o profesional, integrar estas tecnologías de Wiris en tu flujo de trabajo garantiza precisión y eficiencia.
Por ejemplo, para profundizar en el comportamiento de e, se puede visualizar la expresión límite 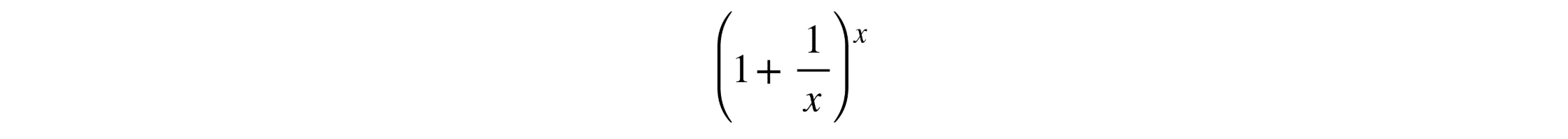 usando herramientas de graficación como CalcMe, un sistema de álgebra computacional (CAS) que permite cálculos complejos de forma rápida e intuitiva. Al aumentar x, la gráfica se aproxima al valor de e, ofreciendo una demostración visual intuitiva de este límite matemático.
usando herramientas de graficación como CalcMe, un sistema de álgebra computacional (CAS) que permite cálculos complejos de forma rápida e intuitiva. Al aumentar x, la gráfica se aproxima al valor de e, ofreciendo una demostración visual intuitiva de este límite matemático.
Además, MathType, el editor de ecuaciones líder en el mundo que permite escribir notación matemática tan fácilmente como texto, facilita la inserción de expresiones complejas en documentos y contenido web, garantizando claridad y precisión.
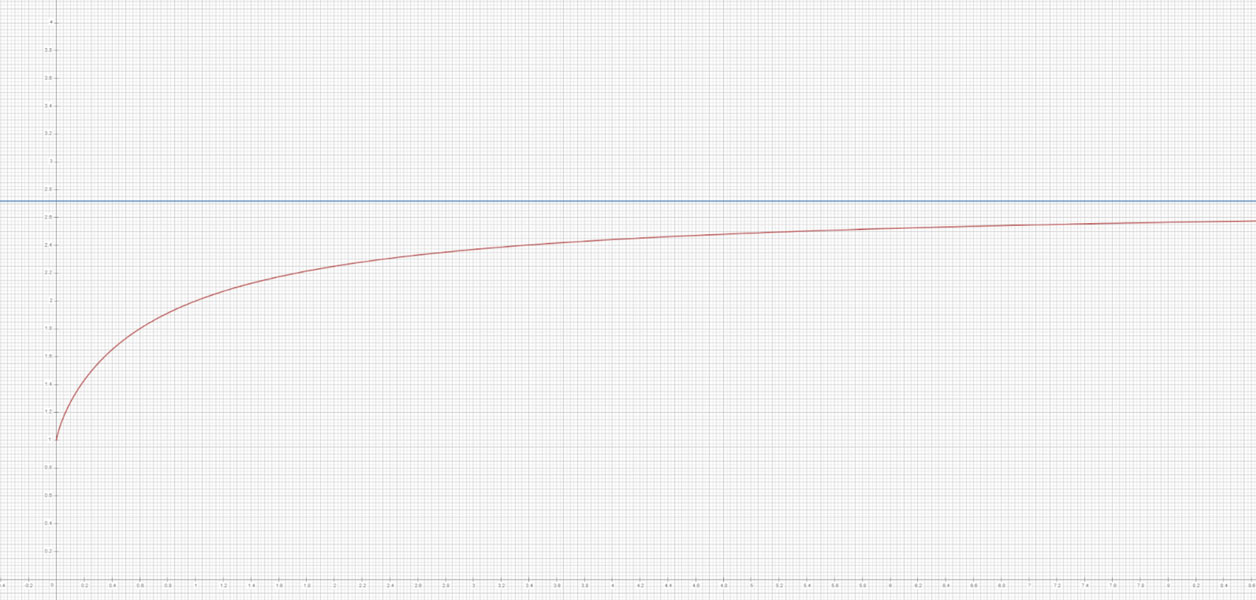
Gráfico que muestra la función (1+1/x)x en rojo, acercándose al valor de e en azul.
Ideal para estudiantes, docentes, editores y redactores técnicos, MathType agiliza la creación de contenido científico y técnico de alta calidad en múltiples plataformas.
Para manejar de forma fluida expresiones matemáticas y visualizaciones, considera incorporar tanto MathType como CalcMe en tu conjunto de herramientas digitales. ¡Escribe aquí tus ecuaciones con el número e!
Compartir










