Solución paso a paso de un problema del examen de
acceso a Oxford.

Cada año, miles de estudiantes se enfrentan al desafío de las pruebas de acceso para ingresar a la prestigiosa Universidad de Oxford, un proceso que pone a prueba no solo su conocimiento, sino también su capacidad de resolución bajo presión. En particular, la prueba de matemáticas es conocida por su complejidad, planteando problemas de todo tipo, desde la resolución de ecuaciones hasta cuestiones de lógica, álgebra avanzada, cálculo y teoría de números. En este artículo, vamos a explorar uno de los problemas presentados en octubre de 2023.

El problema plantea la siguiente pregunta: ¿cuántas soluciones reales tiene la siguiente ecuación?

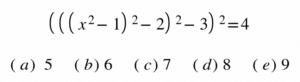
¿Te atreves a resolver la ecuación antes de leer la solución completa en el blog?

A primera vista, el enunciado parece sencillo: una ecuación con una sola variable, donde todos los números involucrados son enteros entre 1 y 4. Sin embargo, la verdadera dificultad radica en deshacer correctamente los paréntesis elevados al cuadrado, asegurándonos de considerar todos los casos posibles.

Un detalle clave en este tipo de ecuaciones es que, al elevar un número al cuadrado, se obtiene el mismo resultado tanto para su valor positivo como para su valor negativo. Por ejemplo:

Esto ocurre porque elevar un número al cuadrado elimina el signo negativo. Por lo tanto, al resolver una ecuación cuadrática debemos tener en cuenta las dos opciones posibles: el número positivo y el negativo que pueden generar ese resultado.

Una última observación: si desarrolláramos completamente los paréntesis, obtendríamos una ecuación de la forma x¹6+… , lo que indica que la ecuación es de grado 16 y, como máximo, podría tener 16 soluciones reales para . Por lo tanto, no podemos descartar ninguna de las opciones que se nos presentan como posibles respuestas.

Dado que para ecuaciones de grado 16 no existe una fórmula sistemática como el método de Ruffini para polinomios de grado 3, resolveremos esta ecuación trabajando los paréntesis de manera progresiva, desde los más externos hacia los más internos.

Ejemplo específico de cómo resolver una ecuación de grado 16

¡Vamos a ello!

Comencemos por el paréntesis más externo. Si definimos t como  as ((x²-1)²-2)²-3 , entonces obtenemos t²=4. Esto nos da dos posibles valores para t: t=2 or t=-2. 

Al sustituir t por su valor original en cada caso, obtenemos los siguientes resultados: 

1.Si t=2 entonces: ((x²-1)²-2)²-3 =2 ⇒ ((x²-1)²-2)²=5 y de nuevo, sustituyendo r= (x²-1)²-2 obtenemos que r²=5 . Veamos los dos nuevos casos que se nos presentan:

1.1 r=√5 sustituyendo r por su valor original obtenemos (x²-1)²-2 =√5 ⇒ (x²-1)²=2+√5 y de nuevo, una última vez, sustituimos s=x²-1, we obtenemos que s²=2+√5 y observamos los dos resultados de nuevo:

Al intentar calcular la raíz cuadrada para obtener el valor de x, estaríamos tomando la raíz de un número negativo. Como resultado, los dos valores obtenidos serán números imaginarios.

1.2 r=-√5 sustituyendo r por su valor original obtenemos (x²-1)²-2=-√5 ⇒ (x²-1)²=2-√5 . Siguiendo el mismo razonamiento que en el apartado anterior, dado que √4=2, se deduce que √5>2 . Esto implica que 2-√5<0, y al intentar calcular su raíz cuadrada, obtendríamos un número imaginario. Por lo tanto, al continuar desarrollando para obtener el valor de x, este también sería un número imaginario.

2. Si t=-2 entonces: ((x²-1)²-2)²-3 =-2 ⇒ ((x²-1)²-2)²=1 y de nuevo,
sustituyendo r= (x²-1)²-2 obtenemos que r²=1 . Veamos los dos casos:

2.1 r=1: sustituyendo r por su valor original obtenemos (x²-1)²-2 =1 ⇒ (x²-1)²=3 y de nuevo, una última vez, sustituimos s=x²-1, y obtenemos que s²=3 y observamos los dos resultados de nuevo:

2.1.1 s=√3 y sustituyendo la por su valor, obtenemos finalmente: x²-1=√3 ⇒ x²=1+√3 y por lo tanto

2.1.2 s=-√3 sustituyendo s por su valor original obtenemos x²-1=-√3 ⇒ x²=1-√3 . Esta resta es negativa, ya que √2≈1,41 y por lo tanto, √3>1,41 con lo que deducimos que 1-√3<0 , y al intentar calcular su raíz cuadrada, obtendríamos un número imaginario.

2.2 r=-1 sustituyendo r por su valor original obtenemos (x²-1)²-2 = -1 ⇒ (x²-1)² = 1 y de nuevo, una última vez, sustituimos s=x²-1 y obtenemos que s²=1 y observamos los dos resultados de nuevo:

2.2.1 s=1 y sustituyendo la s por su valor, obtenemos finalmente: x²-1 = 1 ⇒ x²=2 y por lo tanto

2.2.1.1 x=√2 que es una solución real.

2.2.1.2 x=-√2 que es una solución real.

2.2.2 s=-1 sustituyendo la s por su valor, obtenemos finalmente: x²-1 = -1 ⇒ x²=0 y por lo tanto la única posible solución es x=0 .

Hagamos un repaso de todos los posibles valores reales de x que hemos obtenido:

 

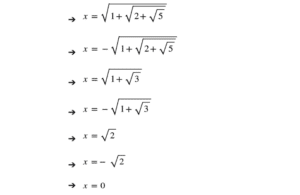
Esto nos da un total de 7 soluciones reales para x, por lo que la respuesta correcta es la opción (c).

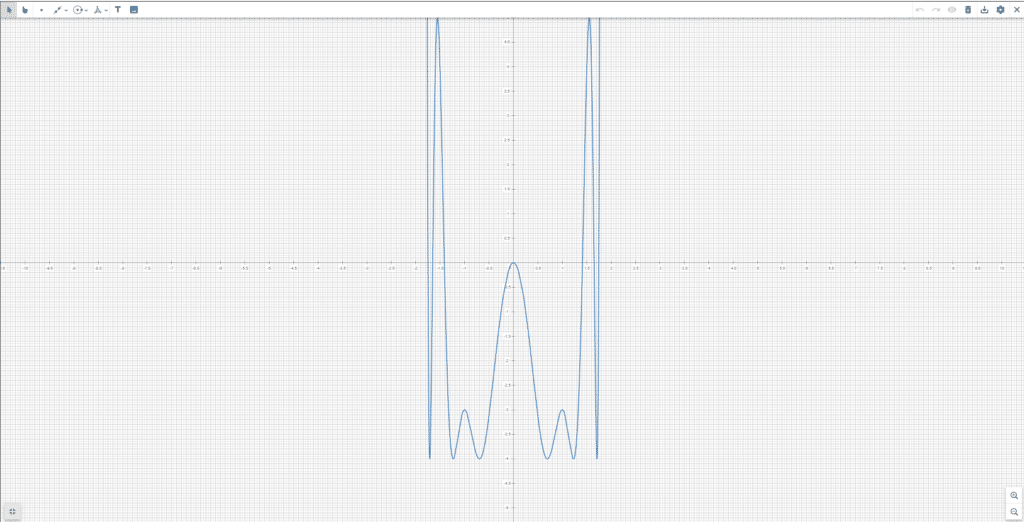
¿Habías acertado tu respuesta? ¿Te atreverás con más retos en el futuro?

Si este contenido te resultó útil o inspirador, ¡compártelo con tus amigos y compañeros amantes de los números!