---

La pandemia ha obligado a las escuelas a adaptarse a la formación en línea.

La pandemia de COVID-19 ha provocado una revolución sin precedentes en la educación. El confinamiento obligó a adaptar las clases a formatos online, lo que supuso un gran reto para muchos profesionales y centros educativos.

Tras casi dos años desde el inicio de la pandemia de COVID-19, es hora de echar la vista atrás y analizar cómo ha vivido la comunidad educativa el impacto de la pandemia y la transformación online. Y nos preguntamos: ¿ha llegado la educación online para quedarse?

El papel de la tecnología

El uso de la tecnología en las aulas ya era una tendencia y una preocupación importante en los centros educativos antes de la pandemia: en Estados Unidos, el 85 % de los administradores de distrito informaron de que el uso de recursos de aprendizaje digitales era una prioridad en 2019, y ya en el curso académico 2017-2018, el 21 % de las escuelas públicas ofrecían al menos un curso en línea. La pandemia obligó a acelerar esta tendencia, y en la primavera de 2020 el 80 % de los hogares con niños estudiaban en línea.

La tecnología ha permitido que la educación continúe mientras las escuelas estaban cerradas, demostrando que puede proporcionar un plan B en momentos de crisis. El uso de plataformas que facilitan videoconferencias, chats y herramientas para compartir documentos proporcionó un canal para impartir aprendizaje a distancia y mantener en contacto a estudiantes y profesores.

Por otro lado, los programas y aplicaciones especializados para trabajar contenidos específicos ayudaron a los estudiantes en una situación en la que tenían que trabajar completamente por su cuenta. Estas herramientas han entrado definitivamente en las aulas y sin duda marcarán la educación del futuro.

MathType es un claro ejemplo de esta situación: el uso del editor de ecuaciones experimentó un enorme crecimiento (más del 400 %) durante los meses de confinamiento estricto. Desde entonces, el número de usuarios que abren documentos con fórmulas no ha dejado de crecer, lo que demuestra que el contenido digital generado durante la pandemia seguirá utilizándose.

Aprendizaje hibrido

Durante la pandemia de COVID-19, casi el 90 % de las instituciones de educación superior europeas adaptaron sus formatos de aprendizaje a modelos en línea o mixtos. Pero incluso ahora que la situación de la pandemia nos permite volver a las clases presenciales, la formación en línea sigue siendo una opción que se puede combinar con la asistencia presencial. Esto se denomina aprendizaje híbrido y aprovecha lo mejor de cada modelo, desde la cercanía y el contacto cara a cara hasta las ventajas que ofrecen los equipos, herramientas y aplicaciones educativos.

El aprendizaje híbrido tiene un gran potencial por explorar. Por ejemplo, podría ayudar a los alumnos enfermos a continuar con sus cursos de forma normal. También podría ser una solución para los colegios de algunas zonas rurales, donde los alumnos tienen que recorrer largas distancias para acudir al colegio cada día. Gracias a la tecnología, el aprendizaje híbrido es un modelo educativo interesante, ya que permite adaptarse fácilmente a las necesidades de cada centro, tipo de alumno y formación.

Retos de la formación online

Sin embargo, los modelos en línea o híbridos también plantean grandes retos para las escuelas y los profesionales de la educación, así como para los estudiantes y sus familias.

Para empezar, no todos los hogares disponen de las herramientas digitales necesarias y de una conexión a Internet estable.

Esto crea una brecha digital que dificulta el acceso a la educación. Además, estas dificultades afectan más duramente a las comunidades educativas vulnerables. Según UNICEF, tres de cada cuatro estudiantes que no pueden acceder a las políticas de aprendizaje a distancia proceden de zonas rurales o pertenecen a los hogares más pobres.

Las condiciones en las que los estudiantes trabajan en casa también son un inconveniente de la educación en línea. Un tercio de los estudiantes de educación superior de la UE no suelen disponer de un lugar tranquilo para estudiar, y casi el 60 % afirma que no siempre cuenta con una conexión a Internet fiable. La experiencia de la pandemia sugiere que, incluso en los países desarrollados, aún queda un largo camino por recorrer hasta que la implementación del aprendizaje a distancia no deje a nadie atrás.

Además, se requieren nuevas habilidades para dominar las tecnologías. Los profesionales de la educación deben adaptarse a estas nuevas herramientas digitales, mientras que los estudiantes deben ser capaces de adquirir las habilidades que promuevan su independencia, flexibilidad y voluntad de aprender y mejorar más allá de los años escolares.

Adaptar el contenido

Otro reto es saber cómo adaptar eficazmente los contenidos al formato online. Impartir clases por videoconferencia o colgar las asignaturas en la nube puede no ser suficiente si esperamos el mismo nivel de resultados. Una proporción significativa de estudiantes de la UE (47,43 %) considera que su rendimiento académico se vio afectado negativamente cuando se cancelaron las clases presenciales, una clara señal de que la tecnología no logró sustituir por completo la educación presencial.

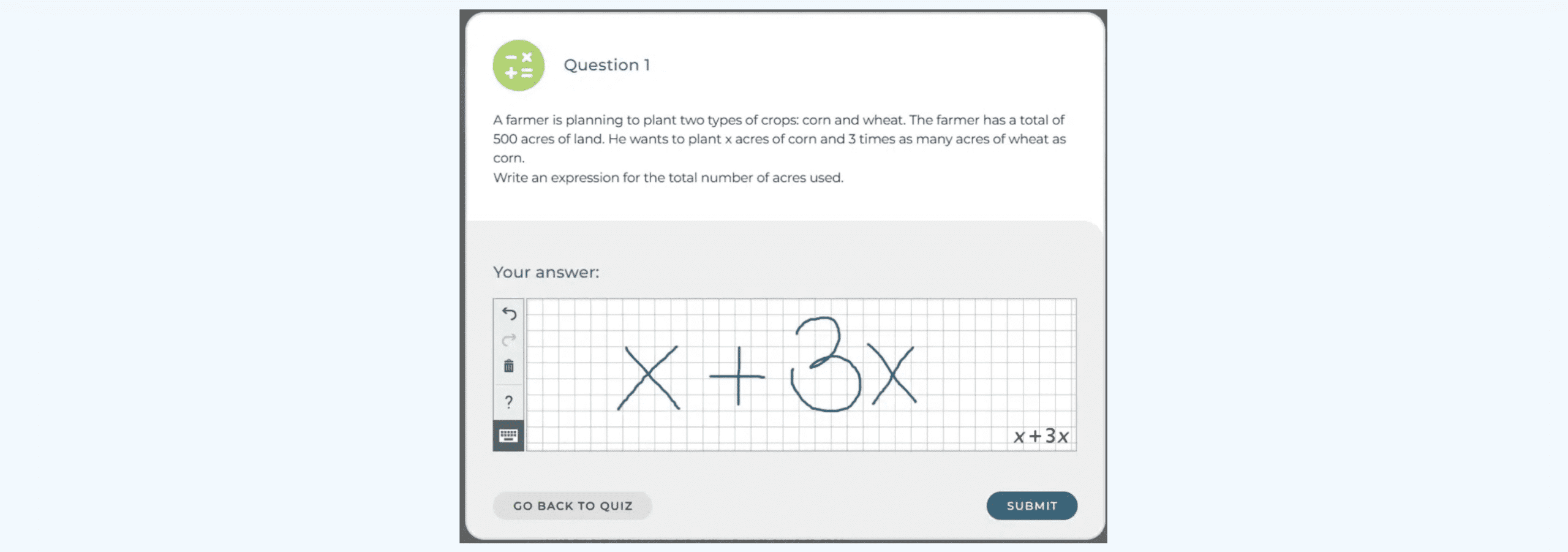
En el modelo digital, los contenidos deben adaptarse mediante aplicaciones y programas que hagan que la materia resulte más atractiva y comprensible. Esto supone un reto especial en las asignaturas STEM, cuyos materiales (gráficos, ecuaciones, trabajos de laboratorio, etc.) son más difíciles de adaptar a un formato en la nube.

Un ejemplo de adaptación exitosa de material tradicional a formato digital son las recientes funciones gráficas de WirisQuizzes, que se crearon durante la pandemia y ahora constituyen un soporte digital para las partes más visuales de las matemáticas: geometría, funciones y estadística.

Aunque existen retos en el aprendizaje en línea, las herramientas y los modelos educativos evolucionarán para superarlos. Todavía queda un largo camino por recorrer, pero la mayoría estaría de acuerdo en que la revolución del aprendizaje en línea ha llegado para quedarse. La siguiente pregunta es: ¿hacia dónde queremos que nos lleve?

 

Fuentes:

• European University Association, European higher education in the Covid-19 crisis.
• World Economic Forum, The COVID-19 pandemic has changed education forever.
• US Census Bureau, Nearly 93% of Households With School-Age Children Report Some Form of Distance Learning During COVID-19.
• European Comission, The impact of COVID-19 on higher education: a review of emerging evidence.
• UNICEF, Promising practices for equitable remote learning.
• Picture: School photo created by freepik – www.freepik.com

Bridging the gap between classrooms and real world 

Los enfoques formulistas y basados en el aprendizaje memorístico de la educación presencial están cada vez más obsoletos en un mundo en rápida evolución e impulsado por la tecnología. A medida que la tecnología avanza a pasos agigantados cada año que pasa, las carreras más gratificantes son aquellas en las que los profesionales pueden utilizar enfoques innovadores y creativos para aplicar lo que han estudiado en los libros de texto.

Tomemos como ejemplo las matemáticas y las ciencias. Vivimos en un mundo complejo en el que todos nuestros hábitos y comportamientos pueden cuantificarse. Queremos saber cuántas horas dormimos, cuántos pasos damos cada día, cómo late nuestro corazón mientras hacemos la compra y cómo responde nuestro cuerpo a un tipo de música. Esta es la era del big data, la analítica, el reconocimiento de patrones y la inteligencia artificial. La educación en el aula puede ser más eficaz si los profesores establecen conexiones significativas entre las lecciones académicas y el mundo real.

Itinerarios personalizados para el aprendizaje

Si la educación puede ser lo suficientemente flexible como para dar cabida a las fortalezas y las inclinaciones de aprendizaje de cada estudiante, se habrá ganado más de la mitad de la batalla. Si los estudiantes cuentan con la capacidad de diseñar su educación y elegir qué aprender y cómo aprender (mediante la toma de decisiones informadas), es probable que se esfuercen más por aprovechar al máximo sus horas de clase y más allá de ellas.

Cada estudiante es único. El sistema educativo debe ser flexible para celebrar esta singularidad y ayudar a los estudiantes a alcanzar sus objetivos profesionales. Esto ya se está haciendo en algunos lugares. Por ejemplo, la Universidad de Leiden, en los Países Bajos, ofrece itinerarios de aprendizaje flexibles en los que los estudiantes pueden hacerse cargo de su educación para adaptarla a sus ambiciones personales. Los profesores les orientarán en la creación de un itinerario educativo único que complemente sus talentos e intereses.

Un alumno puede tener una inclinación natural hacia los números, mientras que otro puede ser bueno para comprender conceptos. Un alumno puede ser rápido para detectar errores, mientras que otro puede ser bueno con las palabras y la escritura. La enseñanza puede ser más eficaz si se optimizan las fortalezas de cada alumno para crear una experiencia de aprendizaje integral.

Un plan de futuro

Las vías de aprendizaje personalizadas tienen beneficios que van más allá de la experiencia de aprendizaje en el aula. Tomemos el ejemplo de Rhiannon Dunn, profesora de noveno grado en la escuela secundaria Science Hill High School de Johnson City, Tennessee (EE. UU.), que ha aplicado el concepto de aprendizaje personalizado que los alumnos pueden elegir por sí mismos. Dunn creó un círculo literario en el que los alumnos tienen la libertad de elegir cualquier libro para su tiempo de lectura independiente. También pueden decidir cómo les evalúa la profesora en esta actividad de aprendizaje. Esto transmite a los alumnos un mensaje claro: ellos tienen voz en su proceso de aprendizaje.

El estudiante se interesa activamente por trazar un plan de acción para el futuro vinculando la educación con la carrera profesional en la que más se ve a sí mismo. Tiene en cuenta sus intereses, sus puntos fuertes naturales y su curiosidad, y los alinea con la profesión que ha elegido. Los estudiantes son capaces de elaborar un plan para su vida profesional y ser proactivos en la toma de decisiones mientras cursan sus estudios.

Dado que los alumnos se responsabilizan de su propia educación, es probable que se interesen más y se impliquen más en el proceso de aprendizaje. De ser observadores pasivos en el aula, se convierten en alumnos activos. Cuando la trayectoria de aprendizaje personalizada de un alumno incluye métodos de enseñanza creativos, lo ideal es que los alumnos continúen aprendiendo también fuera del aula.

¿Qué ocurre si un estudiante cambia de opinión después de un tiempo en la trayectoria? Esto podría suceder, ya que no se puede esperar que los estudiantes sepan con certeza lo que quieren. La trayectoria educativa debe ser lo suficientemente flexible como para permitir que un estudiante explore adiciones o cambios sin sentir que está perdido o que tiene que empezar de cero. Por lo tanto, el asesoramiento educativo es extremadamente importante para garantizar que el estudiante se comprometa y se le permita cierto margen de maniobra para ajustar la trayectoria de aprendizaje.

Inculcar el espíritu de curiosidad

Un enfoque creativo del aprendizaje debe comenzar en el aula, donde los alumnos adquieren la confianza de que el aprendizaje no tiene por qué ser algo fijo o impuesto. Se trata más bien de un proceso que dura toda la vida, que puede ser lúdico y que fomenta el espíritu de investigación del alumno. La curiosidad y el deseo de saber son la base de una educación significativa. Esta curiosidad se ve impulsada por la personalización del aprendizaje, de modo que el alumno puede avanzar a su propio ritmo y en su propio tiempo, utilizando el formato que le da los mejores resultados.

Un camino indicado para cada estudiante

Vivimos en un mundo que cada vez valora más nuestra singularidad y ofrece soluciones personalizadas a nuestras necesidades. Ya sea en publicidad, tecnología, salud, belleza o fitness, la personalización se ha infiltrado en todos los aspectos de nuestra vida. ¿Por qué debería ser diferente en el ámbito educativo?

Trazar un camino único para cada estudiante es una perspectiva emocionante en la que el estudiante, el principal interesado en la educación, tiene la máxima influencia y también el máximo beneficio del proceso.

Fuentes:

• Tennessean, El aprendizaje personalizado puede igualar las oportunidades para los estudiantes de bajos ingresos de Tennessee.
• Tennessean, Nashville PROPEL parents advocate for more personalized learning for their students
• KnowledgeWorks, Creating Personalized, Community-Oriented Learning Pathways
• Edtechmagazine, Boost SEL and Collaboration in the Classroom with 1:1 Devices
• Universiteit Leiden, Flexible learning pathways
• Picture: Study group photo created by freepik – www.freepik.com

 

En los últimos años, las herramientas digitales están ganando popularidad. Al igual que en muchos otros aspectos de la vida, la digitalización está encontrando su lugar en el entorno de los laboratorios. No es de extrañar. La lista de ventajas que supone el cambio al software en línea en el trabajo diario es larga.

Por otro lado, el salto del papel al formato digital puede resultar un poco abrumador en ocasiones. Para ayudarte a tomar una decisión, aquí tienes una lista con cinco razones por las que deberías plantearte dar el paso, si aún no lo has hecho.

1. Flexibilidad

El coronavirus nos ha demostrado lo importante que es poder acceder a tus datos y a tu trabajo cuando estás lejos de tu laboratorio o lugar de trabajo. Ahora que estamos dejando atrás la pandemia, sigue habiendo muchas situaciones en las que necesitamos trabajar a distancia: cuando trabajamos desde casa para mejorar el equilibrio entre la vida laboral y la personal (especialmente importante para resolver la brecha de género 1, 2); cuando estamos en el extranjero para asistir a una conferencia o visitar otro laboratorio; o incluso cuando avanzamos en nuestra carrera y comenzamos un nuevo puesto. En todos estos casos, la flexibilidad del software en línea puede ser una gran ventaja: puedes acceder a él en cualquier momento, en cualquier lugar y desde cualquier dispositivo. Las posibilidades son prácticamente infinitas.

2. Productividad:

Una de las mayores preocupaciones en el ámbito científico es la reproducibilidad. Según una encuesta realizada por Nature* a 1576 investigadores, el 52 % de ellos cree que existe una importante «crisis» de reproducibilidad. En la misma línea, en una encuesta en línea realizada a miembros de la Sociedad Americana de Biólogos Celulares4, más del 70 % de los encuestados afirma haber intentado reproducir un experimento externo sin éxito y, lo que es aún más sorprendente, el 50 % de ellos no ha conseguido reproducir sus propios experimentos.

Las razones detrás de esto son muchas: desde un análisis o diseño experimental deficiente, hasta errores humanos o falta de información completa sobre los métodos. La lista continúa, pero en muchos de estos casos, el uso de software en línea podría ayudar a aumentar la reproducibilidad. Están diseñados para ser consistentes, seguir los estándares de la industria y facilitar los experimentos automatizados y la recopilación de datos.

3. Posibilidad de compartir:

Las herramientas en línea también están diseñadas para compartir fácilmente sus archivos y resultados con colegas y colaboradores. Además de facilitar el mantenimiento de registros y hacerle la vida más fácil, compartir es más importante que nunca. En los últimos años, cada vez más editoriales y financiadores están fomentando, e incluso exigiendo, el depósito de datos brutos y protocolos en un repositorio. En este contexto, el uso de herramientas en línea puede convertirse en una gran ventaja.

Además, mejorar la forma en que comparte sus datos brutos, resultados y protocolos tiene un impacto positivo en la reproducibilidad de sus experimentos. Un estudio publicado en Plos One* indica que compartir datos de investigación detallados se asocia con un aumento en la tasa de citas. Compartir no solo mejora su trabajo, sino también la calidad y solidez de la ciencia en general.

4. Ahorra tiempo

Las herramientas en línea te ayudan a simplificar tu flujo de trabajo y ahorrar tiempo. Aunque en muchos casos puedes hacer el mismo trabajo con lápiz y papel, las versiones en línea lo hacen más rápido. Están diseñadas para liberarte de tareas que suelen ser aburridas y que requieren mucho tiempo, y para mejorar uno o varios pasos clave de un experimento (creación, ejecución, recopilación de datos, procesamiento de datos y cálculos).

Además, el uso de una herramienta ayuda a comparar los resultados de múltiples ejecuciones y, lo que es aún más interesante, cuando se trabaja con grandes cantidades de datos y muestras, puede ayudar a ver los resultados de forma global y encontrar conexiones.

5. Aumentar la productividad:

Por último, pero no menos importante, el uso de herramientas en línea mejora la productividad y la eficiencia. Además de ahorrar tiempo, el uso de software en línea evita los errores y fallos humanos típicos que pueden arruinar un experimento: datos copiados incorrectamente, errores de transcripción, pérdida de datos, almacenamiento aleatorio de registros… También ayudan a optimizar el flujo de trabajo y a automatizar los procesos. En resumen, el uso de herramientas en línea es una forma estupenda de aumentar la productividad en el laboratorio.

Por eso, todo el mundo puede beneficiarse del cambio al software en línea. Desde pequeños laboratorios hasta grandes empresas biotecnológicas. Hay muchas opciones disponibles. Si está pensando en dar el paso, le recomendamos que empiece poco a poco y pruebe diferentes soluciones hasta encontrar la que mejor se adapte a sus necesidades y mejore su flujo de trabajo.

En Wiris, hacemos todo lo posible por crear software químico y herramientas de análisis de resultados que te faciliten la vida para que puedas centrarte realmente en tu investigación.

• The Oxford Student: https://www.oxfordstudent.com/2021/02/25/women-are-still-disadvantaged-in-stem-and-the-pandemic-is-only-making-it-worse/

 

• Forbes: https://www.forbes.com/sites/andrealoubier/2017/03/13/how-working-remotely-is-helping-women-close-the-gender-gap-in-tech/?sh=5a9376bf4ea7

 

• The American Society for Cell Biology: https://www.ascb.org/wp-content/uploads/2015/11/final-survey-results-without-Q11.pdf

• Plos One: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0000308#references

 

¿Cuántas veces hemos oído decir a alguien «no se me dan bien los números» o «las matemáticas me ponen nervioso»? Muchas veces, al parecer. La ansiedad matemática es, en su nivel más básico, el miedo a utilizar números en cualquier forma, ya sea para calcular o para comprender conceptos a través de números y datos, grandes o pequeños.

La Mathematical Association of America ha afirmado que, según algunas estimaciones, el 93 % de los adultos estadounidenses experimentan algún tipo de ansiedad matemática. La ansiedad matemática ha sido estudiada por psicólogos y científicos durante años, y la primera identificación de la «ansiedad numérica» se remonta a 1957.

Los estudios iniciales de la ansiedad matemática intentaron separarla de la ansiedad general y el rendimiento. Si tenemos confianza en las matemáticas, rendimos mejor en ellas. El Programa para la Evaluación Internacional de Estudiantes llevó a cabo un estudio global a gran escala con estudiantes de 15 años de 64 países en 2012. El estudio descubrió que la ansiedad matemática estaba relacionada negativamente con el rendimiento en matemáticas: los estudiantes con altos niveles de ansiedad matemática obtuvieron peores resultados en la asignatura en comparación con aquellos que mostraban niveles más bajos de ansiedad. La ansiedad matemática activa el centro del miedo en el cerebro y bloquea la capacidad de resolución de problemas del estudiante, aunque este sea muy capaz.

El impacto negativo de la ansiedad matemática

La ansiedad matemática es muy real y puede impedir que un estudiante alcance su máximo potencial profesional. Se sabe que la falta de confianza en las matemáticas y las creencias negativas sobre la capacidad innata para los números que se adquieren en los primeros años de vida provocan una ansiedad persistente que se extiende a lo largo de la etapa escolar e incluso más allá. Como resultado, muchos estudiantes dudan en elegir STEM y optan por materias que no implican matemáticas. Aunque puedan tener una gran capacidad para comprender conceptos complicados y la inteligencia necesaria para resolver problemas, los estudiantes evitan las materias STEM para no tener que lidiar con los números a diario.

Igualdad de género

Varios estudios muestran que la ansiedad matemática parece ser mayor en las mujeres que en los hombres, aunque las diferencias relacionadas con el género en cuanto al rendimiento en matemáticas son pequeñas o inexistentes. Esto ilustra que la ansiedad matemática tiene un sesgo de género debido al impacto de los estereotipos de género. Estos estereotipos generan barreras subconscientes entre las niñas, que se consideran menos capaces de rendir bien en matemáticas y STEM.

Matemáticas en el trabajo

Dado que el futuro laboral exige un mayor uso del big data, el análisis de datos y la cuantificación de las experiencias humanas, la necesidad de talento en el ámbito numérico no hará más que aumentar. La Oficina de Estadísticas Laborales de EE. UU. ha estimado que, entre 2016 y 2026, habrá un aumento del 28 % en las profesiones que utilizan las matemáticas. Esto significa que los estudiantes que se sienten cómodos con las matemáticas pueden inclinarse por estas profesiones y tener mejores perspectivas laborales. Pero, ¿qué pasa con aquellos que sufren ansiedad matemática? Tendrán que elegir entre enfrentarse a la ansiedad y superarla, o buscar otras profesiones que no requieran matemáticas.

Superar la ansiedad a las matemáticas

El amor (o el odio) por las matemáticas tiene sus raíces en la infancia. Los padres y los profesores desempeñan un papel crucial a la hora de hacer que las matemáticas sean divertidas para los niños. Pueden hacerlo asegurándose de que su propia ansiedad, si la tienen, no se transmita al niño.

También es importante romper los estereotipos y los imaginarios relacionados con las matemáticas: debemos cambiar la percepción de que las matemáticas son una materia difícil, aburrida y propia de los hombres.

La tecnología puede ayudar a que las matemáticas sean divertidas en el contexto más amplio de los juegos, la resolución de problemas y las actividades de aprendizaje basadas en la diversión. Las aplicaciones y los sitios web con una experiencia interactiva pueden atraer los objetivos de rendimiento de los estudiantes, reduciendo así el miedo a los números.

Para hacer frente a la ansiedad matemática se requiere un enfoque social holístico con una mayor concienciación en todos los puntos de interacción de la educación de los alumnos: el hogar, la escuela, el sistema educativo y el grupo de compañeros. La buena noticia es que la ansiedad matemática se reconoce cada vez más como un problema psicológico. Las soluciones también están al alcance de la mano, si estamos dispuestos a prestar atención.

Fuentes:

• npr.org: Math anxiety is real. Here’s how to help your child avoid it.
• girlsschool.org: The math-anxiety performance link. A global phenomenon.
• Frontiers in psychology: Gender differences regarding the impact of math anxiety on arithmetic performance in second and fourth graders
• Harvard business Review: Americans need to get over their fear of math.