Autor: Aida Alsina

Categorías
Sin categorizar

Retroalimentación instantánea en preguntas abiertas de matemáticas: aprendizajes clave de BETT 2025

Bett congress 2025 Wiris Tech in Action

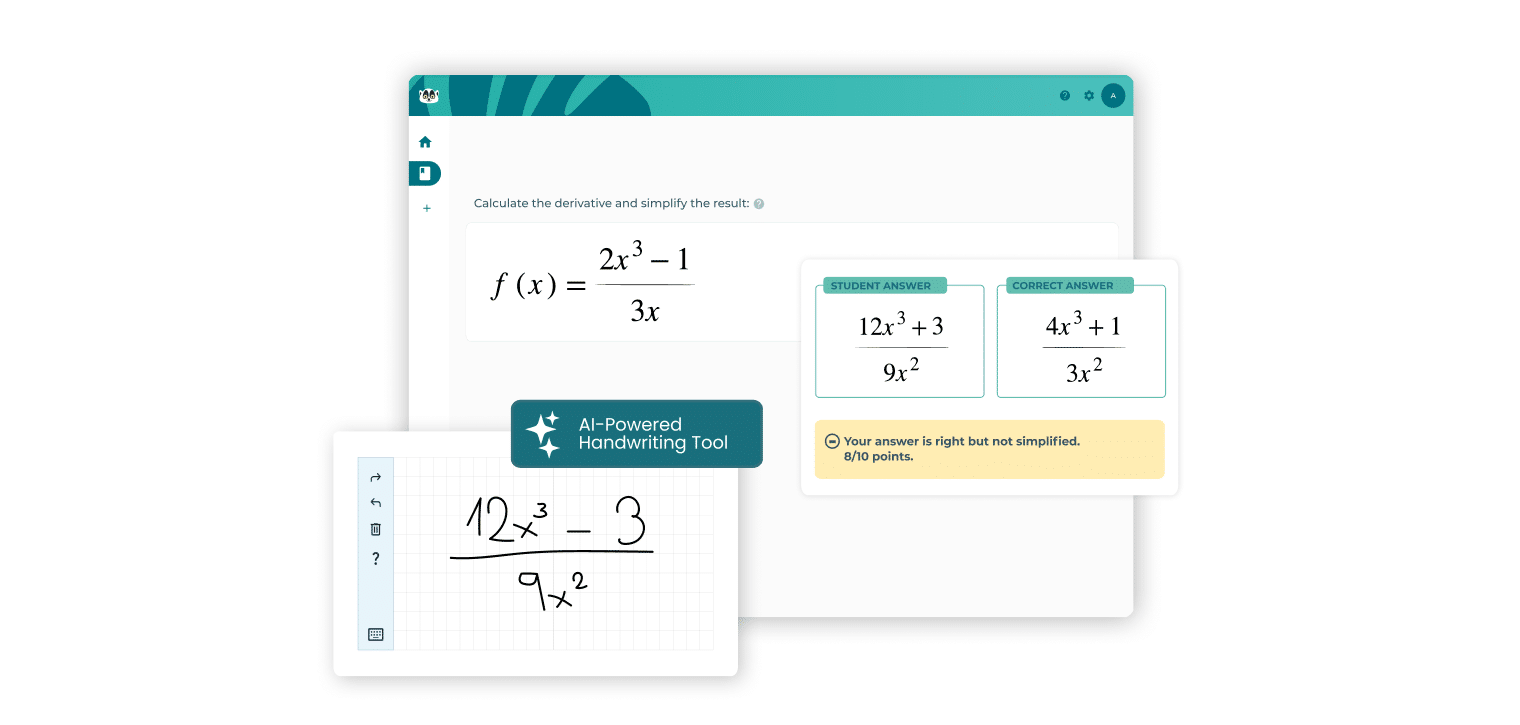
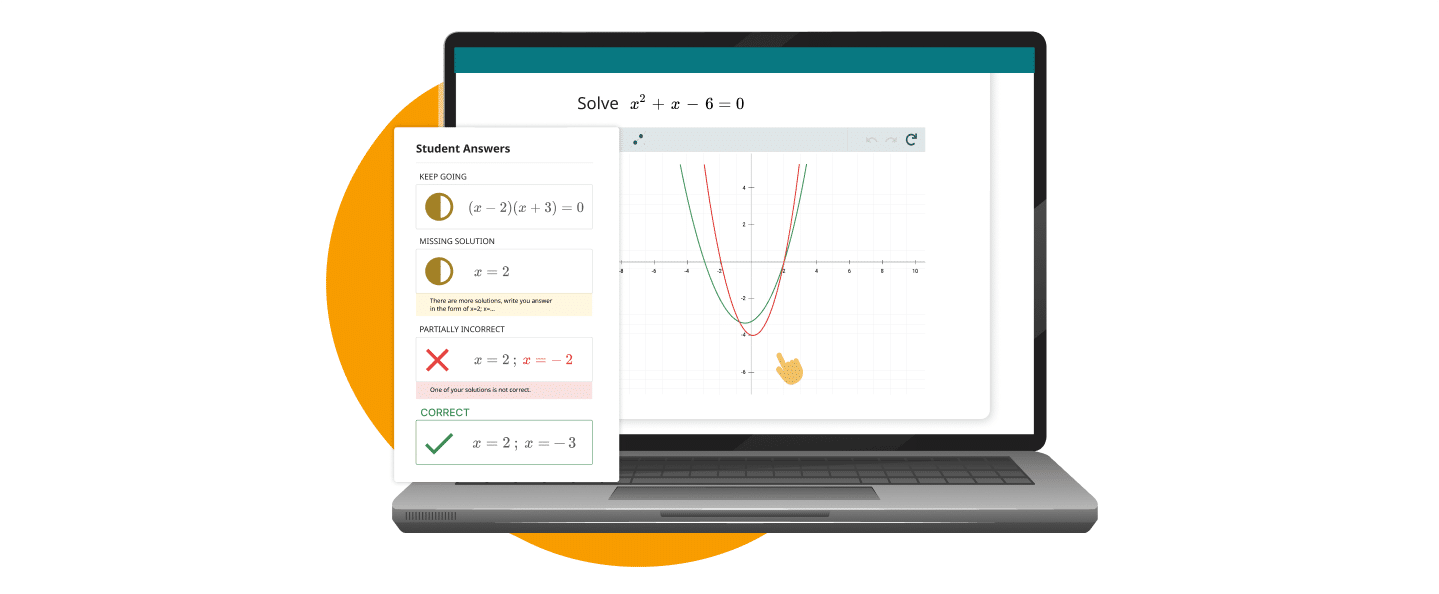
Recientemente tuvimos la emocionante oportunidad de presentar nuestro enfoque en BETT 2025, bajo el título “Enhancing Open-Ended Math Questions with Instant Feedback”, ante profesores, editoriales y educadores en general durante la conferencia en Londres. La retroalimentación juega un papel crucial en guiar el aprendizaje y, en el evento, nos centramos en cómo la retroalimentación instantánea en preguntas abiertas de matemáticas puede mejorar de manera significativa la comprensión matemática de los estudiantes, al mismo tiempo que ayuda a los docentes y hace su día a día más eficiente.

A diferencia de los problemas tradicionales de opción múltiple, las preguntas abiertas en matemáticas requieren un razonamiento más profundo, ya que son preguntas que el alumno puede responder libremente sin un formato predefinido, lo que hace que la retroalimentación personalizada sea aún más importante. En este artículo, exploraremos la importancia de la retroalimentación instantánea en preguntas abiertas de matemáticas y veremos cómo distintos tipos de retroalimentación —correctiva, confirmatoria y sugerente— pueden ayudar a los estudiantes a mejorar.

 

 

Por qué importa la retroalimentación instantánea en preguntas abiertas de matemáticas

El poder de la retroalimentación en el proceso de aprendizaje

La retroalimentación es parte integral del proceso de aprendizaje: ayuda a los estudiantes a refinar su pensamiento y a mejorar su comprensión. Esto es especialmente cierto en las preguntas abiertas de matemáticas, donde a menudo no hay una única respuesta correcta. En estos casos, la retroalimentación instantánea puede marcar una gran diferencia al guiar a los estudiantes hacia la solución adecuada.

Durante BETT 2025, discutimos cómo la retroalimentación instantánea en matemáticas no solo ayuda a los alumnos a corregir errores rápidamente y a ganar confianza, sino también cómo asiste a los profesores en el aula, haciendo que el proceso de enseñanza y aprendizaje sea mucho más eficiente.

Tipos de retroalimentación en preguntas abiertas de matemáticas

Según las necesidades del estudiante y la naturaleza de la pregunta, se requieren diferentes tipos de retroalimentación. Los tres principales que destacamos en BETT 2025 fueron: retroalimentación sugerente, retroalimentación confirmatoria y retroalimentación correctiva.

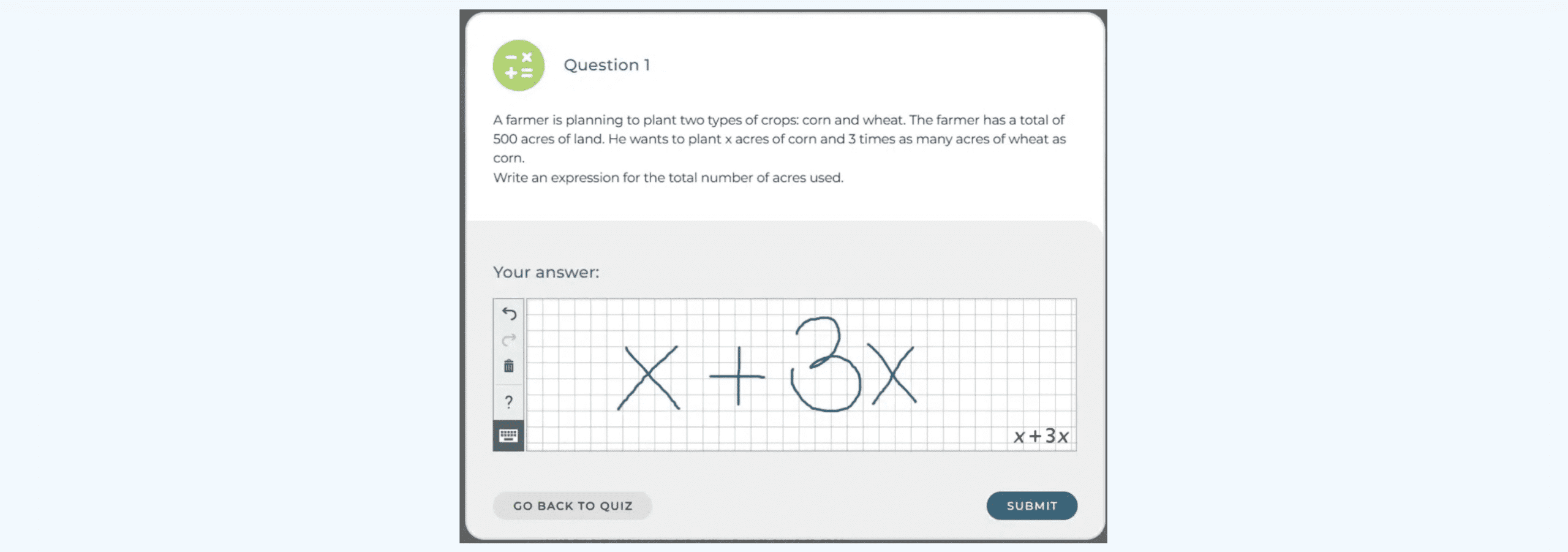
Retroalimentación sugerente en preguntas de matemáticas

La retroalimentación sugerente guía a los estudiantes para que descubran la solución por sí mismos. En lugar de dar la respuesta directamente, fomenta la resolución independiente. Por ejemplo, si un alumno propone “2 y 8” como los dos números cuya suma es 10 y cuyo producto es máximo, la retroalimentación sugerente podría ser: “¿Qué ocurre si pruebas con números más cercanos entre sí?”.

 

Retroalimentación confirmatoria en preguntas de matemáticas

La retroalimentación confirmatoria está diseñada para reforzar respuestas correctas. Cuando los estudiantes resuelven problemas adecuadamente, comentarios como “¡Correcto, bien hecho!” sirven para afirmar su comprensión y aumentar su confianza.

En el caso de las preguntas abiertas, la retroalimentación confirmatoria es especialmente valiosa para asegurar que los estudiantes se mantengan motivados, incluso cuando trabajan en problemas complejos.

Este tipo de retroalimentación fomenta el pensamiento crítico y la exploración, convirtiéndose en una herramienta
esencial para el desarrollo de habilidades de resolución de problemas en preguntas abiertas de matemáticas.

Retroalimentación correctiva en preguntas de matemáticas

La retroalimentación correctiva identifica los errores y proporciona la respuesta correcta. Por ejemplo, si un alumno resuelve incorrectamente la ecuación x^2 = 4 como x = 4, la retroalimentación correctiva sería: “La solución correcta es x = ±2”.

Si bien es eficaz para aclarar malentendidos, debe usarse con moderación, ya que depender demasiado de este tipo de retroalimentación puede limitar el desarrollo de habilidades de resolución de problemas.

 

 

El ciclo de enseñanza: un marco para la aplicación de la retroalimentación

En BETT 2025, Mrs. Brook, una profesora ficticia de secundaria, compartió su ciclo de enseñanza, que integra de manera fluida la retroalimentación correctiva, sugerente y confirmatoria. Su ciclo está diseñado para maximizar los resultados de aprendizaje al alinear las estrategias de retroalimentación con las distintas etapas de la enseñanza.

Las cuatro etapas del ciclo de enseñanza de Mrs. Brook

  • Presentación del contenido

Mrs. Brook comienza la clase introduciendo y explicando el tema a sus estudiantes. Este paso asegura que todos tengan una comprensión básica del contenido.

  • Validación del conocimiento al final de la clase

Tras la lección, Mrs. Brook realiza una comprobación de conocimientos. Aquí la retroalimentación correctiva desempeña un papel crucial. Por ejemplo, si un alumno malinterpreta un concepto o cálculo, la profesora ofrece retroalimentación correctiva inmediata para aclarar los errores.

 

  • Recomendación de práctica en casa:

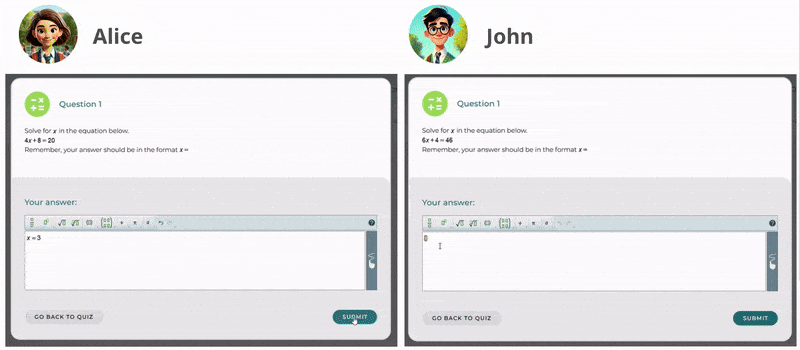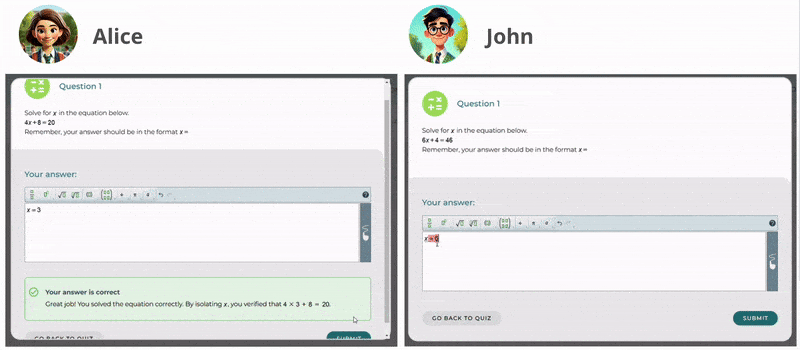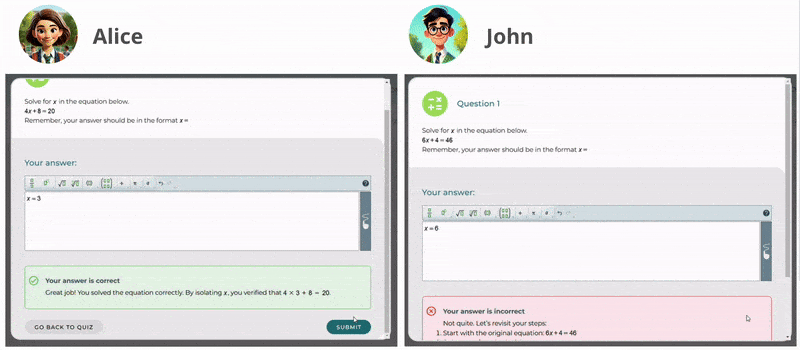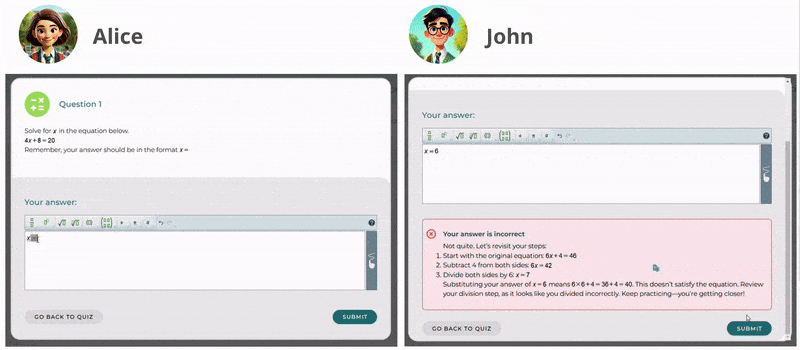
Mrs. Brook anima a sus alumnos a practicar de manera independiente. En esta etapa, emplea a menudo retroalimentación sugerente para guiarlos sin darles directamente las respuestas, ayudándolos a pensar de forma crítica y a explorar soluciones. Además, utiliza retroalimentación confirmatoria para reforzar las soluciones correctas y aumentar la confianza del alumnado. Cuando los estudiantes resuelven con éxito un problema, ella ofrece refuerzos positivos como “¡Muy bien hecho!” para motivarlos y afirmar su comprensión.

 

  • Evaluación del nivel de conocimiento de los estudiantes

Tras haber practicado, Mrs. Brook evalúa el progreso de sus alumnos para identificar áreas de mejora. En esta fase, fomenta la reflexión sobre el propio proceso de aprendizaje y anima a continuar creciendo. Mantiene un entorno positivo reconociendo los esfuerzos y ofreciendo motivación para que los estudiantes sigan comprometidos y seguros de sus habilidades.

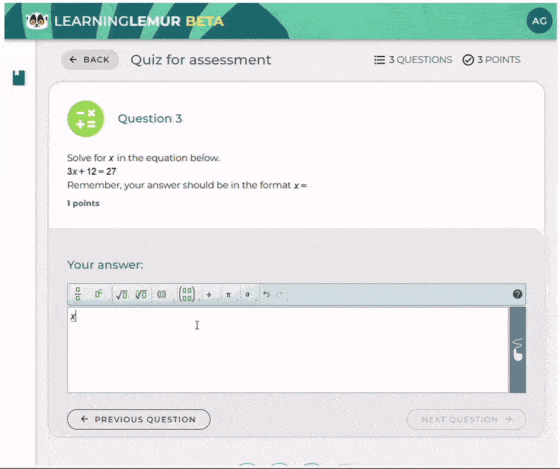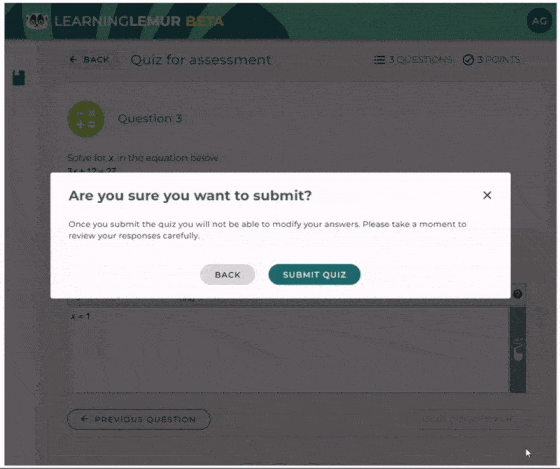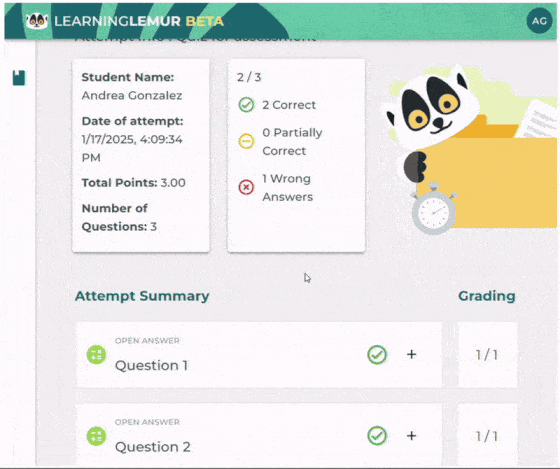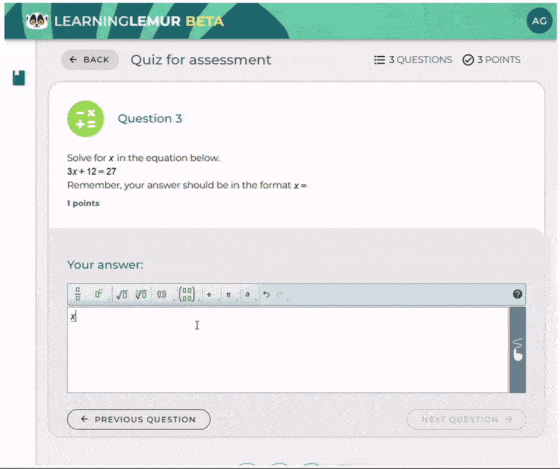
Este modelo cíclico de enseñanza y retroalimentación demuestra cómo un enfoque estructurado puede potenciar el aprendizaje y asegurar que se atiendan las necesidades de los estudiantes en cada etapa.

 

 

Adoptando el futuro de la enseñanza de las matemáticas con Wiris

En WIRIS estamos comprometidos a apoyar a los educadores con las herramientas que necesitan para ofrecer una retroalimentación eficaz. Nuestros productos LearningLemur y WirisQuizzes garantizan que la retroalimentación instantánea en preguntas abiertas de matemáticas sea accesible y personalizable, ayudando a los estudiantes a progresar en su aprendizaje.

A medida que la tecnología sigue evolucionando, la integración de la retroalimentación instantánea en las preguntas abiertas será cada vez más crítica. Esperamos con entusiasmo la evolución continua de la enseñanza de las matemáticas, impulsada por el aprendizaje personalizado y la retroalimentación en tiempo real.

Pruébalo ahora

 

Categorías
Sin categorizar

Cómo resolver una ecuación de grado 16

Solución paso a paso de un problema del examen de
acceso a Oxford.

Cada año, miles de estudiantes se enfrentan al desafío de las pruebas de acceso para ingresar a la prestigiosa Universidad de Oxford, un proceso que pone a prueba no solo su conocimiento, sino también su capacidad de resolución bajo presión. En particular, la prueba de matemáticas es conocida por su complejidad, planteando problemas de todo tipo, desde la resolución de ecuaciones hasta cuestiones de lógica, álgebra avanzada, cálculo y teoría de números. En este artículo, vamos a explorar uno de los problemas presentados en octubre de 2023.

El problema plantea la siguiente pregunta: ¿cuántas soluciones reales tiene la siguiente ecuación?

¿Te atreves a resolver la ecuación antes de leer la solución completa en el blog?

A primera vista, el enunciado parece sencillo: una ecuación con una sola variable, donde todos los números involucrados son enteros entre 1 y 4. Sin embargo, la verdadera dificultad radica en deshacer correctamente los paréntesis elevados al cuadrado, asegurándonos de considerar todos los casos posibles.

Un detalle clave en este tipo de ecuaciones es que, al elevar un número al cuadrado, se obtiene el mismo resultado tanto para su valor positivo como para su valor negativo. Por ejemplo:

Esto ocurre porque elevar un número al cuadrado elimina el signo negativo. Por lo tanto, al resolver una ecuación cuadrática debemos tener en cuenta las dos opciones posibles: el número positivo y el negativo que pueden generar ese resultado.

Una última observación: si desarrolláramos completamente los paréntesis, obtendríamos una ecuación de la forma x¹6+… , lo que indica que la ecuación es de grado 16 y, como máximo, podría tener 16 soluciones reales para . Por lo tanto, no podemos descartar ninguna de las opciones que se nos presentan como posibles respuestas.

Dado que para ecuaciones de grado 16 no existe una fórmula sistemática como el método de Ruffini para polinomios de grado 3, resolveremos esta ecuación trabajando los paréntesis de manera progresiva, desde los más externos hacia los más internos.

Ejemplo específico de cómo resolver una ecuación de grado 16

¡Vamos a ello!

Comencemos por el paréntesis más externo. Si definimos t como  as ((x²-1)²-2)²-3 , entonces obtenemos t²=4. Esto nos da dos posibles valores para t: t=2 or t=-2. 

Al sustituir t por su valor original en cada caso, obtenemos los siguientes resultados: 

1.Si t=2 entonces: ((x²-1)²-2)²-3 =2 ⇒ ((x²-1)²-2)²=5 y de nuevo, sustituyendo r= (x²-1)²-2 obtenemos que r²=5 . Veamos los dos nuevos casos que se nos presentan:

1.1 r=√5 sustituyendo r por su valor original obtenemos (x²-1)²-2 =√5 ⇒ (x²-1)²=2+√5 y de nuevo, una última vez, sustituimos s=x²-1, we obtenemos que s²=2+√5 y observamos los dos resultados de nuevo:

Al intentar calcular la raíz cuadrada para obtener el valor de x, estaríamos tomando la raíz de un número negativo. Como resultado, los dos valores obtenidos serán números imaginarios.

1.2 r=-√5 sustituyendo r por su valor original obtenemos (x²-1)²-2=-√5 ⇒ (x²-1)²=2-√5 . Siguiendo el mismo razonamiento que en el apartado anterior, dado que √4=2, se deduce que √5>2 . Esto implica que 2-√5<0, y al intentar calcular su raíz cuadrada, obtendríamos un número imaginario. Por lo tanto, al continuar desarrollando para obtener el valor de x, este también sería un número imaginario.

2. Si t=-2 entonces: ((x²-1)²-2)²-3 =-2 ⇒ ((x²-1)²-2)²=1 y de nuevo,
sustituyendo r= (x²-1)²-2 obtenemos que r²=1 . Veamos los dos casos:

2.1 r=1: sustituyendo r por su valor original obtenemos (x²-1)²-2 =1 ⇒ (x²-1)²=3 y de nuevo, una última vez, sustituimos s=x²-1, y obtenemos que s²=3 y observamos los dos resultados de nuevo:

2.1.1 s=√3 y sustituyendo la por su valor, obtenemos finalmente: x²-1=√3 ⇒ x²=1+√3 y por lo tanto

2.1.2 s=-√3 sustituyendo s por su valor original obtenemos x²-1=-√3 ⇒ x²=1-√3 . Esta resta es negativa, ya que √2≈1,41 y por lo tanto, √3>1,41 con lo que deducimos que 1-√3<0 , y al intentar calcular su raíz cuadrada, obtendríamos un número imaginario.

2.2 r=-1 sustituyendo r por su valor original obtenemos (x²-1)²-2 = -1 ⇒ (x²-1)² = 1 y de nuevo, una última vez, sustituimos s=x²-1 y obtenemos que s²=1 y observamos los dos resultados de nuevo:

2.2.1 s=1 y sustituyendo la s por su valor, obtenemos finalmente: x²-1 = 1 ⇒ x²=2 y por lo tanto

2.2.1.1 x=√2 que es una solución real.

2.2.1.2 x=-√2 que es una solución real.

2.2.2 s=-1 sustituyendo la s por su valor, obtenemos finalmente: x²-1 = -1 ⇒ x²=0 y por lo tanto la única posible solución es x=0 .

Hagamos un repaso de todos los posibles valores reales de x que hemos obtenido:

 

Esto nos da un total de 7 soluciones reales para x, por lo que la respuesta correcta es la opción (c).

¿Habías acertado tu respuesta? ¿Te atreverás con más retos en el futuro?

Si este contenido te resultó útil o inspirador, ¡compártelo con tus amigos y compañeros amantes de los números!

Categorías
Sin categorizar

MathType Math Equation Writer se une a la App Store educacional de Skolon

Un nuevo capítulo para MathType: ahora en Skolon

Wiris se complace en anunciar que MathType, nuestro reconocido editor de ecuaciones matemáticas para crear y editar ecuaciones matemáticas, ya está disponible en la app store educativa de Skolon. Esta asociación marca un hito importante en nuestra misión de simplificar la enseñanza de las matemáticas para estudiantes y profesores de todo el mundo. Con funciones que mejoran el formato del contenido matemático, MathType mejora la forma en que se presentan y se comprenden las expresiones matemáticas en los entornos de aprendizaje digital.

¿Qué significa esto para los educadores y los estudiantes?

A través de la plataforma de Skolon, los educadores pueden integrar perfectamente el editor de ecuaciones de MathType en sus recursos didácticos. Con su interfaz intuitiva y sus potentes funciones, MathType hace que sea más fácil que nunca crear ecuaciones y notaciones matemáticas de calidad profesional. Para los estudiantes, esta herramienta proporciona una forma accesible de abordar las matemáticas complejas, lo que fomenta una comprensión más profunda de la materia. Además, sus herramientas de formato garantizan que las expresiones matemáticas sigan siendo claras y estén bien estructuradas en diferentes contextos digitales.

¿Por qué elegir MathType Math Equation Writer en Skolon?

Al unir fuerzas con Skolon, nos aseguramos de que los educadores y los estudiantes tengan fácil acceso a las capacidades del editor de ecuaciones matemáticas de MathType. La plataforma de Skolon simplifica el proceso de descubrir, comprar e implementar herramientas educativas, lo que la convierte en un socio ideal para ofrecer las ventajas de MathType a un público más amplio. Ahora, las escuelas pueden adoptar rápidamente MathType como parte de su ecosistema de aprendizaje digital, optimizando tanto la enseñanza como el aprendizaje. Con funciones mejoradas de formato y compatibilidad, MathType mejora aún más la claridad del contenido matemático en múltiples formatos.

Acerca de la “App Store” educativa de Skolon

Skolon es una marca de confianza en el ámbito de la tecnología educativa en el norte de Europa, que ofrece una “App Store” completa que satisface las diversas necesidades de las escuelas y los educadores. Su plataforma permite a los usuarios acceder y gestionar una amplia gama de herramientas digitales en un único y cómodo lugar, y nos enorgullece ver el editor de ecuaciones matemáticas MathType entre sus productos de confianza. La capacidad de generar expresiones matemáticas claras y estructuradas garantiza que el contenido matemático digital siga siendo visualmente preciso y fácil de compartir.

Empiece a utilizar MathType hoy mismo

Le invitamos a explorar MathType en Skolon y a experimentar de primera mano cómo su editor de ecuaciones matemáticas puede mejorar sus esfuerzos educativos. Tanto si es un profesor que desea enriquecer su plan de estudios como si es un estudiante que busca una mejor manera de abordar las matemáticas, MathType en Skolon está aquí para ayudarle. Con opciones de formato avanzadas, MathType garantiza la claridad matemática en todas las plataformas digitales.

Descubre ahora MathType en Skolon

Mirando hacia el futuro

En Wiris, nos comprometemos a potenciar el sector educativo a través de herramientas innovadoras como MathType. La colaboración con Skolon nos acerca a nuestro objetivo de hacer que las matemáticas sean accesibles, atractivas y divertidas para todos. Aprovechando el editor de ecuaciones matemáticas de MathType y sus funciones de presentación mejoradas, seguimos mejorando el aprendizaje digital en todo el mundo.

Estate atento a más novedades, ya que seguimos ampliando nuestro alcance y mejorando las experiencias de aprendizaje a nivel mundial.

Categorías
Sin categorizar

Conjetura de Collatz

Conjetura de Collatz

Las conjeturas matemáticas son enigmas que desafían la mente humana: problemas aparentemente sencillos que, a pesar de haberse verificado en millones de casos, aún carecen de una demostración. Son pregunta aparentemente intuitivas que esconden una complejidad inesperada.

Lo fascinante de las conjeturas es que, en muchos casos, se pueden verificar empíricamente, es decir, comprobarse mediante una cantidad enorme de ejemplos numéricos. Sin embargo, esta comprobación no satisface a los matemáticos, quienes buscan una demostración teórica, una prueba sólida que valide el enunciado en su totalidad. Sin dicha demostración, las conjeturas permanecen como retos abiertos.

La conjetura de Collatz es un ejemplo perfecto de este tipo de misterio matemático. Fue propuesta en 1937 por Lothar Collatz y su enunciado es el siguiente:

Escogiendo un número entero positivo cualquiera aplicaremos los siguientes pasos:

➔ Si el número es par, lo dividiremos entre 2.

➔ Si el número es impar, lo multiplicaremos por 3 y luego le sumaremos 1.

➔ Repetiremos el proceso con el nuevo número obtenido

La conjetura dice que, sin importar el número con el que empieces, siempre llegarás al número 1. Una vez que llegas al 1, el proceso se repite indefinidamente: 1 →4 →2 →1

Formalmente, esto se puede escribir como la función f=N →N definida como:

Dos ejemplos ilustrativos de la Conjetura de Collatz

Veamos un par de ejemplos sencillos.

Tomemos el número n=6 y apliquemos los pasos de la conjetura de Collatz:

  1. 6 es par así que lo dividimos entre 2: 6/2=3
  2. 3 es impar por lo que multiplicamos por 3 y le sumamos 1: 3·3+1=10
  3. 10 es par así que lo dividimos entre 2: 10/2=5
  4. 5 es impar por lo que multiplicamos por 3 y le sumamos 1: 3·5+1=16
  5. 16 es par así que lo dividimos entre 2: 16/2=8
  6. 8 es par así que lo dividimos entre 2: 8/2=4
  7. 4 es par así que lo dividimos entre 2: 4/2=2
  8. 2 es par así que lo dividimos entre 2: 2/2=1

Una vez que llegamos a 1, el proceso se repite: 1 →4 →2 →1.

Así que observamos que comenzando con n=6 la conjetura se satisface.

Tomemos ahora el número n=21 y apliquemos los pasos de la conjetura de Collatz:

  1. 21 es impar por lo que multiplicamos por 3 y le sumamos 1: 21·3+1=64
  2. 64 es par así que lo dividimos entre 2: 64/2=32
  3. 32 es par así que lo dividimos entre 2: 32/2=16
  4. 16 es par así que lo dividimos entre 2: 16/2=8
  5. 8 es par así que lo dividimos entre 2: 8/2=4
  6. 4 es par así que lo dividimos entre 2: 4/2=2
  7. 2 es par así que lo dividimos entre 2: 2/2=1

De nuevo, llegamos al número 1.

Ambos ejemplos han llegado al número 1, pero en un número distinto de pasos. De hecho, aunque 21 es un número mayor, llegó a 1 en menos pasos que 6. Esta conjetura ha sido probada para una increíble cantidad de números, hasta más de 2ˆ60 = 1.152.921.504.606.846.976 casos, sin encontrar ningún contraejemplo. Sin embargo, aún sigue siendo un misterio si existe algún número que no cumpla la conjetura.

Representaciones gráficas de la conjetura de Collatz

El grafo dirigido de órbitas es una representación visual que facilita la comprensión del comportamiento de los números bajo las reglas de la conjetura de Collatz. En este gráfico, cada número se representa como un nodo, y las conexiones entre ellos muestran los pasos que sigue el proceso de la conjetura. Al seguir la secuencia de un número, los nodos se conectan mediante flechas que indican cómo se transforma el número en cada paso. Aunque en general se omiten los números pares en la representación para simplificar, el gráfico ilustra cómo los números «orbitan» alrededor de ciertos ciclos, como el 1 →4 →2 →1.

En la imagen anterior, podemos ver un ejemplo del grafo dirigido de órbitas, donde hemos resaltado en amarillo los números 3 y 21. El número 3 hace referencia a la secuencia del 6, ya que en este gráfico se omiten los números pares para simplificar la visualización.

Observamos que el 21 llega rápidamente a 1, ya que solo pasa por números pares en su camino, como vimos en el ejemplo anterior. Por otro lado, el número 6 primero se convierte en 3, luego pasa por el número 5, que finalmente lo llevará a 1 tras varios pasos con números pares.

También es interesante notar que el número 9, aunque relativamente pequeño, sigue una secuencia más larga: pasa por los números 7, 11, 17, 13 y 5, y finalmente llega a 1, tras un total de 19 pasos.

A continuación, se presenta un gráfico en el que el eje X muestra los distintos valores enteros iniciales, mientras que el eje Y representa el número de iteraciones necesarias para que cada número alcance el valor 1.

En resumen, la conjetura de Collatz es un problema aparentemente sencillo que, a día de hoy, aún no tiene una demostración formal. Aunque pueda parecer un enunciado de poca relevancia o utilidad práctica, esta conjetura tiene aplicaciones en diversos campos, como la teoría de números, la criptografía, el análisis de algoritmos y la inteligencia artificial. En estos campos, el estudio de secuencias complejas y su comportamiento bajo reglas específicas puede ofrecer valiosos insights para resolver problemas más mayores y entender patrones matemáticos.

¿Te ha fascinado la simplicidad y el misterio de la conjetura de Collatz? Ahora es tu turno: toma el número 27 y comienza la sucesión. ¿Cuántos pasos necesitarás para llegar al 1?

Si este desafío te atrapó, ¡no lo guardes solo para ti! Compártelo con otros curiosos de los enigmas matemáticos y descubrid juntos quién resuelve el reto más rápido.

Categorías
Sin categorizar

Gamificación en el Aprendizaje de Matemáticas: ¿Mejora el Aprendizaje?

Teenager playing learning

Gamificación en el Aprendizaje de Matemáticas: Beneficios y Retos

¿Dificultad para mantener la atención del alumnado? La gamificación, entendida como el uso de mecánicas de juego en el aprendizaje, ayuda a incrementar la motivación, la comprensión y la retención. La abstracción de conceptos y la dificultad de vincularlos a situaciones reales puede generar desinterés, frustración e incluso ansiedad. En este contexto, la gamificación surge como una estrategia innovadora que busca transformar la experiencia educativa al integrar elementos de juego en el proceso de enseñanza.

Pero, ¿qué es exactamente la gamificación y qué impacto tiene en la enseñanza de las matemáticas? Según Deterding et al. (2011), se define como el uso de elementos de diseño de juegos en contextos no lúdicos para potenciar la participación, la motivación y el compromiso de las personas. En el ámbito educativo, esto implica no solo incorporar mecánicas como desafíos, retroalimentación inmediata, puntos y recompensas, sino también crear experiencias dinámicas e interactivas que fomenten la exploración y el aprendizaje activo.

A lo largo de este artículo exploraremos la evidencia existente sobre la efectividad de la gamificación en la enseñanza de matemáticas y veremos cómo juegos interactivos como Learning Lemur pueden beneficiar el aprendizaje del alumnado.

Por qué Funciona la Gamificación: Beneficios Clave en Matemáticas

La gamificación ha demostrado ser una herramienta eficaz para mejorar la experiencia de aprendizaje en distintas disciplinas, y las matemáticas no son una excepción. Su impacto va más allá de hacer las clases más entretenidas: influye en aspectos clave como la motivación, la comprensión de conceptos y el desarrollo de habilidades cognitivas y sociales. A continuación, se destacan algunos beneficios principales respaldados por la investigación.

Mayor Motivación e Implicación

Uno de los grandes retos en la enseñanza de las matemáticas es mantener el interés del alumnado, especialmente cuando perciben los ejercicios como repetitivos o difíciles. La gamificación transforma estas tareas en experiencias interactivas y estimulantes. Según un estudio de Hamari, Koivisto y Sarsa (2014), la implementación de estrategias gamificadas incrementa significativamente la motivación y el rendimiento académico en diversas disciplinas, incluidas las matemáticas.

Mejor Comprensión y Retención de Conceptos

Los juegos permiten al alumnado interactuar con conceptos matemáticos de forma práctica y visual, facilitando una comprensión más profunda. En lugar de memorizar fórmulas sin contexto, pueden experimentar con problemas en escenarios dinámicos. Un estudio de Wouters et al. (2013) indica que los entornos gamificados no solo mejoran la retención de conocimientos, sino que también fortalecen la capacidad de aplicar lo aprendido en distintas situaciones.

Desarrollo de Habilidades Cognitivas y Sociales

Más allá de los contenidos matemáticos, la gamificación promueve habilidades esenciales para el pensamiento crítico y la resolución de problemas. Resolver desafíos en un entorno gamificado requiere analizar, explorar estrategias y adaptar el enfoque según los resultados. Además, muchas experiencias gamificadas incluyen dinámicas colaborativas que fomentan la comunicación y el trabajo en equipo. También favorece la resiliencia, al permitir aprender de los errores sin el temor al fracaso académico convencional.

Reducción de la Ansiedad Matemática

La ansiedad matemática es un problema común que afecta al rendimiento y la actitud hacia la materia. Presentar problemas en un formato lúdico y menos estructurado puede reducir la presión del aprendizaje formal. Según Sailer et al. (2017), la gamificación ayuda a generar una relación más positiva con las matemáticas, permitiendo afrontar los retos sin miedo al fracaso. La retroalimentación inmediata y los sistemas de recompensas refuerzan el progreso individual, fortaleciendo la confianza y la autonomía en el aprendizaje.

Retos de la Gamificación: Lo que Docentes Deben Saber

Aunque la gamificación ofrece múltiples beneficios, su eficacia depende en gran medida del diseño e implementación. Algunos factores clave a considerar son:

  • Diseño de contenido adecuado: Requiere tiempo y planificación para crear actividades alineadas con los objetivos curriculares.
  • Equilibrio entre juego y aprendizaje: Es esencial que la diversión no eclipse el contenido educativo. El progreso en el juego debe depender del dominio de los conceptos matemáticos.
  • Adaptabilidad: Cada estudiante aprende a su propio ritmo y de manera distinta. Una aproximación gamificada eficaz debe ser flexible y permitir la personalización según niveles y estilos de aprendizaje.

Estrategias para una Gamificación Eficaz en Matemáticas

Para maximizar el potencial de la gamificación en matemáticas, los educadores y desarrolladores deben estructurar cuidadosamente su enfoque. A continuación se presentan algunas estrategias clave para garantizar una implementación eficaz:

Definir Objetivos Claros de Aprendizaje

Toda implementación de gamificación debe tener un propósito educativo definido. Antes de incorporar elementos de juego, es fundamental establecer los resultados de aprendizaje esperados. Cada reto, recompensa o elemento interactivo debe contribuir directamente a la comprensión de los conceptos matemáticos. Cuando los juegos se diseñan en línea con los objetivos curriculares, el alumnado se mantiene motivado mientras progresa académicamente.

Incorporar Juegos Interactivos para Aumentar la Participación

Involucrar al alumnado mediante experiencias interactivas es una de las formas más eficaces de mejorar el aprendizaje. Plataformas digitales y aplicaciones ofrecen retos adaptativos ajustados al nivel de cada estudiante. Características como tablas de clasificación, insignias y logros generan sensación de logro y motivan a persistir en la resolución de problemas matemáticos.

Proporcionar Retroalimentación Inmediata y Seguimiento del Progreso

La retroalimentación oportuna es esencial en el proceso de aprendizaje. Una de las grandes ventajas de la gamificación es ofrecer resultados inmediatos sobre el desempeño. Esto permite identificar errores, ajustar estrategias y reforzar la comprensión. Muchas plataformas digitales incluyen herramientas de seguimiento que ayudan a estudiantes y docentes a monitorear avances, detectar debilidades y celebrar logros.

Fomentar la Colaboración y la Competencia Sana

El aprendizaje gamificado no se limita al progreso individual, también fomenta la interacción social. Los retos cooperativos y la resolución de problemas en equipo enriquecen la experiencia matemática. Al mismo tiempo, la competencia amistosa mediante rankings y sistemas de puntuación motiva al alumnado a superarse de forma constructiva.

Herramientas y Recursos para Gamificar las Matemáticas

Con los avances tecnológicos, existen numerosas herramientas que facilitan la gamificación en matemáticas. Algunas de ellas son:

  • Plataformas digitales de aprendizaje: Sitios web y apps que integran la práctica matemática con juegos.
  • Kits de gamificación para el aula: Recursos físicos y digitales que ayudan al profesorado a implementar dinámicas de juego.
  • Realidad virtual y aumentada: Experiencias inmersivas que permiten interacciones prácticas y visuales con conceptos abstractos.
  • Plugins personalizables para LMS: Herramientas que permiten personalizar la enseñanza con elementos de juego.

Prueba la Gamificación en Matemáticas con Learning Lemur

Los beneficios de la gamificación en matemáticas son claros: mayor motivación, mejor comprensión y un compromiso reforzado. Si quieres experimentar el poder de los juegos interactivos en educación, explora Learning Lemur. Nuestra plataforma permite a docentes y estudiantes sumergirse en experiencias de aprendizaje basadas en el juego.

¡Crea una cuenta gratuita hoy mismo y descubre cómo la gamificación puede revolucionar la forma de aprender matemáticas!

Empieza ahora gratuitamente

Categorías
Sin categorizar

¿Qué es la paradoja del cumpleaños?

birthday paradox

La fascinante probabilidad de compartir fecha

La paradoja del cumpleaños es uno de esos conceptos matemáticos que nos invitan a desafiar nuestra intuición. Una paradoja, en esencia, es una afirmación o resultado que, aunque aparentemente contradictorio o contrario a la lógica común, se demuestra como cierto cuando se analiza detenidamente. En el caso de la paradoja del cumpleaños, el escenario es simple pero desconcertante: ¿cuántas personas deben estar en una sala para que la probabilidad de que al menos dos compartan el mismo cumpleaños sea mayor al 50%?

El resultado será sorprendentemente bajo, pero ¿te atreves a contestar antes de seguir leyendo y revelar la respuesta?

Lo más intuitivo sería pensar que se necesitan al menos 183 personas, la mitad de los días del año, para que la probabilidad de que dos personas compartan el mismo cumpleaños sea mayor al 50%. Sin embargo, la realidad es muy diferente.

Para entender cómo se calcula esta probabilidad, recordemos que la fórmula básica de cualquier probabilidad consiste en dividir los casos favorables entre los casos totales.

En este caso, en lugar de calcular directamente la probabilidad de coincidencia, es más sencillo comenzar calculando la probabilidad de que ninguna persona comparta cumpleaños con otra. Una vez que tenemos esta probabilidad, podemos restarla a 1 para obtener la probabilidad de coincidencia.

Para calcular la probabilidad de que ninguna persona comparta cumpleaños con otra, procederemos de forma constructiva, evaluando escenario por escenario.

  • Si en una sala solo hay una persona, no existe la posibilidad de que comparta su cumpleaños con alguien más, ya que no hay otras personas presentes. Por lo tanto, la probabilidad de que su cumpleaños sea único es del 100%, es decir 365/365.
  • Ahora, si entra una segunda persona, la probabilidad de que su cumpleaños sea diferente al de la primera es 364/365, ya que solo hay 364 días restantes en los que puede nacer para evitar una coincidencia.
  • Si se agrega una tercera persona, la probabilidad de que su cumpleaños no coincida con los de las dos primeras personas es 363/365, ya que ahora hay dos días ocupados.

Por lo tanto, para n personas, se deben cumplir todas las condiciones anteriores de forma simultánea: que la segunda persona no comparta cumpleaños con la primera, que la tercera no comparta con las dos anteriores, y así sucesivamente. Esto implica que la probabilidad de que ninguna de las n personas comparta el mismo cumpleaños es el producto de las probabilidades individuales:

Y finalmente obtenemos:

Analizando probabilidades para distintos valores de n

Examinemos los resultados para diferentes valores de n:

  • Para n=10 obtenemos que P (almenos una coincidencia) = 11,61%

CalcMe representation of the equation

This calculation has been created using CalcMe
  • Para n=15 obtenemos que P (almenos una coincidencia) = 25,03%
  • Para n=23 obtenemos que P (almenos una coincidencia) = 50,05%
  • Para n=50 obtenemos que P (almenos una coincidencia) = 96,53%
  • Para n=60 obtenemos que P (almenos una coincidencia) = 99,22%

Como podemos observar en los ejemplos anteriores, para alcanzar una probabilidad superior al 50%, solo se necesitan 23 personas en una misma sala. Este resultado puede parecer sorprendente, pero tiene sentido si consideramos que con 23 personas se pueden formar 253 pares diferentes, y cada uno de estos pares representa una oportunidad para que dos personas compartan el mismo cumpleaños. Aún más sorprendente es que para tener una probabilidad superior al 99%, sólo se necesitan 60 personas, lo que demuestra cómo el número de combinaciones posibles crece rápidamente con cada nueva persona añadida.

Esta es la gráfica de la distribución de probabilidad:

Graph showing the probability of two people sharing a birthday, with the number of people on the X-axis and the probability on the Y-axis, expressed as a percentage.
Gráfico que muestra la probabilidad de que dos personas compartan cumpleaños, con el número de personas en el eje X y la probabilidad en el eje Y, expresada en porcentaje.

En contraste, si en lugar de calcular la probabilidad de coincidencia entre cualquier par de personas consideramos la probabilidad de que alguien en una sala de n personas (excluyéndote a ti) comparta específicamente tu cumpleaños, el cálculo es diferente. Esta probabilidad está dada por:

P(alguien con el mismo cumpleaños que tu) =1-(364/365)

Para n=22, esta probabilidad es de aproximadamente 0.059 (5.9%), lo cual es bastante baja. De hecho, sería necesario que hubiera al menos 253 personas en la sala para que esta probabilidad supere el 50%.

La paradoja del cumpleaños es un recordatorio fascinante de cómo nuestra intuición puede fallar frente a la lógica matemática.

Ahora que conoces la paradoja del cumpleaños y sus conceptos clave, ¿puedes calcular la probabilidad de que exactamente k personas dentro de un grupo de n personas compartan su cumpleaños? ¡Nos encantaría conocer tus resultados en los comentarios del blog! Si el artículo te ha sorprendido, compártelo con tus amigos para que también descubran esta curiosidad matemática. Además, si te interesa probar estos cálculos por ti mismo, echa un vistazo a CalcMe.

 

Prueba CalcMe

Categorías
Sin categorizar

Wiris en el aula: Aprende y practica con ejercicios ilimitados

Aprender matemáticas requiere más que solo entender teorías: la clave para dominar conceptos complejos y perfeccionar habilidades está en la práctica continua. Sin embargo, los métodos tradicionales a menudo limitan el proceso de aprendizaje: una vez que el estudiante ha resuelto un problema, el desafío desaparece, y los exámenes suelen repetir las mismas preguntas, perdiendo así su valor como herramienta de evaluación. Imagina tener la posibilidad de generar ejercicios ilimitados con variables aleatorias, adaptados a las necesidades de cada estudiante. Con Wiris, esto ya es posible.

Además, cuenta con corrección automática, lo que significa que, mientras se genera el ejercicio, se calcula la respuesta de forma simultánea. Esto permite recibir retroalimentación al instante, facilitando el aprendizaje y la corrección de errores de manera inmediata.

Para los profesores, esta herramienta ofrece una ventaja clave: la posibilidad de generar una cantidad infinita de ejercicios, cada uno único. De este modo, los docentes pueden crear experiencias de aprendizaje variadas y personalizadas, garantizando que los alumnos enfrenten nuevos retos en cada práctica.

Por su parte, los estudiantes disfrutan de una práctica constante que les permite reforzar sus habilidades sin la preocupación de repetir los mismos ejercicios. Además, esta capacidad de generar ejercicios ilimitados les ofrece una excelente preparación para los exámenes.

Ejemplo práctico: Resolución de un sistema de ecuaciones lineales

Para ilustrar cómo funciona esta herramienta y cómo puede ser utilizada en el aula, vamos a centrarnos en la resolución de sistemas de ecuaciones lineales. Elegimos este tipo de problemas porque representan un reto matemático común al que se enfrentan todos los estudiantes y ofrecen la posibilidad de explorar diferentes métodos de resolución. Además, los sistemas de ecuaciones pueden tener diversas características, como ser compatibles, incompatibles o indeterminados, permitiendo a los estudiantes trabajar con una amplia gama de situaciones.

Imaginemos que tenemos el siguiente sistema de ecuaciones lineales de tres incógnitas:

Vamos a resolverlo utilizando el Método de Gauss. El primer paso es escribir el sistema en forma de matriz aumentada:

Ahora vamos a aplicar operaciones elementales para reducir la matriz a su forma escalonada.

Por lo que obtenemos:

A partir de la ecuación 3 del sistema, encontramos la variable :

Generación ilimitada de sistemas de ecuaciones lineales con
variables aleatorias

Ahora que hemos resuelto este sistema, para seguir practicando, nos gustaría poder generar nuevos sistemas de ecuaciones de la misma forma, pero con valores aleatorios.

Estos sistemas tendrían la forma siguiente:

A continuación, te mostramos un ejemplo de código para implementar esta funcionalidad y generar sistemas de ecuaciones aleatorios determinados. ¡Con Wiris, es totalmente posible!

r() := random(-4,4)

sol = [r() with i in 1..3]

[a,b,c] = sol

repeat 

A = [[r() with i in 1..3] with j in 1..3]

until determinant (A) != 0 

b = A * sol

ec = {}

for i in 1..3 do

ecaux = A.i * [x,y,z]

ec = append(ec, ecaux = b.i)

end

{ec1, ec2, ec3} = ec

r() := random(-4,4): Esta función genera un número aleatorio entre -4 y 4.

sol = [r() with i in 1..3]: Aquí, se generan tres valores aleatorios que representarán las soluciones del sistema de ecuaciones.

[a,b,c] = sol: Los valores generados se asignan a las incógnitas del sistema.

repeat…until determinant(A) != 0: Este bloque asegura que la matriz de coeficientes A sea invertible (es decir, que su determinante no sea cero), lo que garantiza que el sistema tiene una solución única.

b = A * sol: Se calcula el vector de resultados b multiplicando la matriz de coeficientes A por las soluciones sol.

for i in 1..3 do: En este ciclo se generan las tres ecuaciones, usando cada una de las filas de la matriz A y las soluciones sol.

{ec1, ec2, ec3} = ec: Finalmente, las tres ecuaciones generadas se almacenan en las variables ec1, ec2 y ec3, listos para ser utilizados en nuevos ejercicios.

Utilizando WirisQuizzes e implementando este código como pregunta, podemos obtener los siguientes resultados:

Al recargar otro sistema con el símbolo «=» se genera un nuevo conjunto de ecuaciones, como se muestra a continuación:

Para obtener más detalles, puedes consultar toda la documentación del producto aquí.

Si te ha sido útil, te invitamos a compartirlo con otros compañeros, compañeras, profesores o alumnos. Además, estaremos encantados de conocer tu opinión y cualquier sugerencia que puedas tener.

Descubre WirisQuizzes

Categorías
Sin categorizar

IA en matemáticas: La revolución en la escritura científica

La inteligencia artificial (IA) es un campo de la informática que busca desarrollar sistemas capaces de realizar tareas que tradicionalmente requieren inteligencia humana, como el razonamiento lógico, la resolución de problemas y el aprendizaje. Basada en algoritmos avanzados y modelos de aprendizaje automático, la IA puede analizar grandes volúmenes de datos, identificar patrones complejos y adaptarse de forma autónoma a nuevos contextos.

En matemáticas, estas capacidades están transformando la manera en que se genera, verifica y comunica el conocimiento. Desde la automatización de demostraciones hasta la creación de explicaciones detalladas, la IA está facilitando el trabajo de investigadores, docentes y estudiantes. Además, su capacidad para procesar lenguaje natural está mejorando la redacción de artículos matemáticos, volviéndolos más accesibles, precisos y estructurados.

En este artículo exploraremos cómo la IA en matemáticas está revolucionando la escritura científica y cómo las herramientas de Wiris forman parte de este avance.

El rol de la IA en matemáticas y la creación y edición de contenido matemático

La redacción de artículos científicos en matemáticas siempre ha sido un reto debido a la complejidad de sus notaciones y símbolos. Tradicionalmente, los matemáticos han dependido de la escritura manual o de lenguajes de tipografía complejos. Sin embargo, con la llegada de la IA, el proceso de creación y edición de documentos científicos ha evolucionado exponencialmente.

La inteligencia artificial ha aportado múltiples beneficios a la escritura matemática, facilitando tanto la redacción como la edición y publicación de artículos académicos. A continuación, se describen algunas de las principales formas en que la IA está impactando este ámbito.

Reconocimiento de escritura manual

Uno de los avances más significativos ha sido el desarrollo de sistemas capaces de interpretar y digitalizar notas manuscritas. Tradicionalmente, los matemáticos escribían sus ecuaciones y demostraciones en papel, lo que suponía invertir mucho tiempo si era necesario transcribirlas a formato digital. Con herramientas basadas en IA, como las integradas en MathType, ahora es posible escribir ecuaciones directamente en dispositivos táctiles y convertirlas automáticamente en texto digital editable.

Esto no solo ahorra tiempo, sino que también reduce errores de transcripción y permite trabajar de manera más eficiente. Además, esta tecnología es especialmente útil para estudiantes y docentes, ya que facilita la conversión de apuntes en documentos organizados sin necesidad de mecanografía manual.

Automatización de fórmulas

En la creación de artículos matemáticos, la escritura precisa de fórmulas es esencial. Tradicionalmente, esto requería herramientas especializadas que, aunque potentes, podían resultar complejas y demandaban un conocimiento profundo de su sintaxis, como LaTeX. Los avances tecnológicos han permitido desarrollar herramientas como MathType, que simplifican la redacción de ecuaciones sin necesidad de programación. En lugar de memorizar comandos, los usuarios pueden introducir fórmulas mediante una interfaz gráfica intuitiva. Esto democratiza el acceso a la escritura matemática, permitiendo a más personas crear documentos de calidad sin necesidad de experiencia técnica avanzada.

Otro aspecto clave es la corrección automática de errores en las ecuaciones. La IA en matemáticas puede identificar inconsistencias y sugerir correcciones en tiempo real, evitando errores que podrían comprometer la validez de un artículo académico.

Optimización de la edición

Otro beneficio aportado por la IA es la optimización en la edición de documentos matemáticos. En el pasado, era necesario revisar manualmente posibles errores en ecuaciones, notación y estructura textual. Hoy en día, algoritmos de IA integrados en programas de edición analizan la consistencia de las expresiones, sugieren mejoras y detectan inconsistencias.

Los asistentes de escritura basados en IA, como los integrados en procesadores de texto avanzados, ayudan a mejorar la claridad y la legibilidad de los artículos matemáticos. Además, ofrecen recomendaciones estilísticas para dar al documento una estructura lógica y fácil de seguir, algo crucial en la escritura académica.

La integración de la IA en la escritura matemática no es solo una evolución, sino una revolución que está transformando la manera en que creamos, editamos y compartimos conocimiento científico. Herramientas como las de Wiris, con sus potentes capacidades, están haciendo que la escritura matemática sea más accesible, eficiente y libre de errores. A medida que estas tecnologías continúen avanzando, se reducirá aún más la brecha entre la intuición humana y la precisión de las máquinas, facilitando el trabajo de investigadores, docentes y estudiantes por igual.

Si te ha resultado interesante esta exploración, compártela con tus colegas y únete a la conversación sobre el futuro de la IA en matemáticas.

Para más información sobre nuestros productos, no dudes en ponerte en contacto con nuestro equipo de Ventas en sales@wiris.com.

Categorías
Sin categorizar

Torres de Hanoi: Un desafío de matemáticas y programación

Tower of Hanoi

Torres de Hanoi: Un desafío de matemáticas y programación

Las Torres de Hanoi son uno de los rompecabezas más emblemáticos en el ámbito de las matemáticas y la teoría de la computación. Con su estructura sencilla y reglas claras, este problema ha cautivado a matemáticos y aficionados por igual, convirtiéndose en un reto intrigante desde su creación.

Según la leyenda, las Torres de Hanoi fueron concebidas por un grupo de monjes en un antiguo templo de la India. En el centro de este templo, se erigían tres pilares de oro sobre los que descansaban 64 discos de diferentes tamaños, dispuestos en el primer pilar de manera ordenada: el disco más grande en la base, y sobre él, discos de tamaños progresivamente más pequeños, hasta llegar al disco más pequeño, colocado en la parte superior.

El objetivo de los monjes era mover todos los discos del primer pilar al tercero, usando el pilar central como auxiliar. Para cumplir esta tarea, debían seguir un conjunto de reglas estrictas:

  1. Solo se puede mover un disco a la vez.
  2. Un disco nunca puede colocarse sobre otro más pequeño.

Cuenta la leyenda, que cuando todos los discos fuesen trasladados correctamente al último pilar, el mundo llegaría a su fin. Sin embargo, ¿qué tan cerca está el fin del mundo, realmente?

¿Cuánto tiempo tomaría cumplir con este desafío? Este desafío fue introducido oficialmente por el matemático francés Édouard Lucas en 1883, como parte de sus investigaciones en teoría de números y rápidamente se convirtió en un problema popular.

A continuación, analizaremos la resolución de este problema desde una perspectiva matemática, desglosando sus principios clave, y exploraremos cómo se transforma en un interesante desafío de programación.

Image of the Towers of Hanoi, showing three lines with three pillars pillars with disks of different sizes stacked on the different pillars in order

 

La recursión como solución al rompecabezas

El reto de las Torres de Hanoi no solo está en mover los discos de un pilar a otro, siguiendo las reglas estrictas, sino en cuántos movimientos son necesarios para resolver el problema de trasladar discos desde el pilar de origen al pilar de destino.

La forma más eficiente de abordar este problema es a través de la recursión, una técnica fundamental en programació. La recursión permite dividir el problema en subproblemas pequeños, donde la solución de cada subproblema lleva a la solución del problema original.

En el caso de las Torres de Hanoi, la recursión se aplica de manera natural y podemos dividir el problema de mover discos en tres etapas:

➔ Mover los primeros n-1 discos del pilar de origen al pilar auxiliar, usando el pilar de destino como auxiliar.
➔ Mover el disco más grande (el disco n) del pilar de origen al pilar de destino.
➔ Mover los discos n-1 del pilar auxiliar al pilar de destino, utilizando el pilar de origen como auxiliar.

Este patrón se repite recursivamente, reduciendo el número de discos en cada paso hasta llegar a un caso base, donde solo queda un disco que se mueve directamente.

En términos matemáticos, el número mínimo de movimientos para resolver el problema con n discos es el mismo que el número de movimientos para discos n-1, más uno para mover el disco más grande, más el número de movimientos para discos n-1 otra vez. Esta fórmula da como resultado:

TH( n ) = TH( n – 1 ) + 1 + TH( n – 1 ) = 2TH( n – 1 ) + 1

Donde TH( n ) representa el número de movimientos para n discos.

A partir de la fórmula anterior, iremos sustituyendo cada TH( i ) por su expresión correspondiente hasta llegar a TH( 1 ). Después sustituiremos TH( 1 ) por 1, ya que, con un solo disco, es posible moverlo directamente al pilar de destino, lo que justifica que el número mínimo de movimientos en este caso sea 1.

Veamos la expresión desarrollada:

  • Sustituimos primero TH( n – 1 ), y obtenemos: 

TH( n ) = 2TH( n – 1 ) + 1 

TH( n ) = 2( 2TH( n – 2 ) + 1 ) + 1 = 2²TH( n – 2 ) + 3

  • Ahora sustituimos TH( n – 2 ):

TH( n ) = 2²TH( n – 2 ) + 3

TH( n ) = 2²( 2TH( n – 3 ) + 1 ) + 3 = 2³TH( n – 3 ) + 7

  • Si seguimos sustituyendo de esta forma, llegaremos a una fórmula general:

TH( n ) = 2k  TH( n – k ) + (2k – 1)

Donde k es el número de pasos que damos hacia atrás en la recursión.

  • Para k = n – 1 llegaremos a TH( 1 ), el caso base:

TH( n ) = 2²TH( n – 2 ) + 3

Sabemos que TH( 1 ) = 1, entonces obtenemos:

TH( n ) = 2n – 1 · 1 + ( 2n – 1 – 1 ) = 2n – 1

Hemos demostrado que el número de movimientos necesarios para resolver las Torres de Hanoi con n discos es:

TH( n ) = 2n – 1

Solución mediante inducción matemática

Otra manera de abordar la solución al rompecabezas de las Torres de Hanoi es utilizando inducción matemática, una técnica utilizada para demostrar que una afirmación es cierta para todos los números naturales, basándose en dos pasos fundamentales: el caso base y el paso inductivo.

En este caso, el objetivo es demostrar que para mover discos del primer pilar al tercero, se requieren 2n – 1  movimientos. Vamos a desglosar este proceso con una demostración por inducción.

Caso base:

Supongamos que tenemos solo un disco . En este escenario, es evidente que solo se necesita un movimiento para trasladar el disco desde el pilar de origen al pilar de destino. Es decir, para n = 1, el número de movimientos necesarios es 21 – 1 = 1, lo cual es cierto.

Paso inductivo:

Ahora, supongamos que la afirmación es cierta para n = k, es decir, que para mover k discos se necesitan 2k – 1 movimientos. Lo que debemos demostrar es que la afirmación también se cumple para n = k + 1.

Para mover k + 1 discos, primero necesitamos mover los discos superiores del pilar de origen al pilar auxiliar, utilizando el pilar de destino como auxiliar. Según nuestra hipótesis inductiva, esto tomará 2k – 1 movimientos.

Luego, movemos el disco más grande (el disco  k + 1) del pilar de origen al pilar de destino, lo cual requiere 1 movimiento.

Finalmente, movemos los k discos del pilar auxiliar al pilar de destino, utilizando el pilar de origen como auxiliar, lo que también tomará 2k – 1 movimientos, según nuestra hipótesis inductiva.

Por lo tanto, el total de movimientos necesarios para mover k + 1 discos es:

(2k – 1) + 1 + (2k – 1) = 2k+1 – 1

De esta forma, hemos demostrado que si la afirmación es cierta para n = k, también lo es para n = k + 1.

Como hemos observado que es cierto para 1, mediante inducción matemática podemos concluir que para n discos, el número mínimo de movimientos necesarios es 2n – 1.

Volviendo a la leyenda, si los monjes fueran extremadamente rápidos y pudieran mover un disco en tan solo un segundo, tendríamos que calcular cuántos segundos tomarían para completar el desafío con 64 discos. Según la fórmula 264 – 1, el número total de movimientos sería aproximadamente 18,4 quintillones de movimientos. Si asumimos que cada movimiento toma 1 segundo, esto nos da 18,4 quintillones de segundos. Si convertimos estos segundos en años, obtenemos que el tiempo total sería de aproximadamente 581,4 mil millones de años. Así que, si seguimos la leyenda al pie de la letra, ¡el fin del mundo estaría a una distancia increíblemente lejana!

CalcMe formula

Observamos que la función que describe el número de movimientos necesarios para resolver las Torres de Hanoi es exponencial, lo que significa que crece rápidamente a medida que aumentamos el número de discos. En el siguiente gráfico, podemos ver visualmente cómo esta función se dispara, ilustrando claramente el crecimiento exponencial.

graphic formula

Este soporte visual nos permite confirmar, una vez más, que completar el desafío con 64 discos llevaría un tiempo verdaderamente impresionante.

Si te ha gustado este desafío matemático y te ha sorprendido su solución ¡no dudes en compartir este artículo! Y si te atreves, pon a prueba tus habilidades resolviendo el rompecabezas de las Torres de Hanoi. ¿Lograrás mover los discos en el número exacto de pasos ? ¡Cuéntanos tu experiencia!

Categorías
Sin categorizar

Estudiantes motivados, mejores resultados: La plataforma de aprendizaje de matemáticas de La Salle con WirisQuizzes

De los libros de texto a una plataforma digital personalizada de matemáticas

Cuando La Salle San Ildefonso decidió sustituir los libros impresos de matemáticas por herramientas digitales, necesitaban algo más que simples hojas de trabajo en línea: necesitaban una plataforma completa de aprendizaje de matemáticas. Con WirisQuizzes integrado en Moodle, sus profesores construyeron un sistema colaborativo que fomenta el aprendizaje independiente, la retroalimentación personalizada y la evaluación escalable.

Lo que comenzó como la iniciativa de un profesor se ha convertido en un modelo adoptado en múltiples campus de La Salle, transformando la forma en que los estudiantes se relacionan con las matemáticas.

El desafío

Cuando La Salle San Ildefonso decidió eliminar los libros de texto físicos de matemáticas, se enfrentaron a una pregunta crítica: ¿cómo ofrecer un aprendizaje de matemáticas de alta calidad en un formato completamente digital sin sacrificar retroalimentación, rigor ni accesibilidad?

Como explicó el profesor Javier Melchior, las primeras herramientas digitales ofrecían poco más que una calificación binaria de correcto o incorrecto.

“Lo único que podíamos decir era si la respuesta estaba bien o mal. Y eso no era suficiente”, explicó Javier. “Lo que los estudiantes necesitaban era orientación: no solo la solución, sino el cómo llegar a ella”.

Esta idea se convirtió en un punto de inflexión para el enfoque digital de La Salle. No se trataba solo de digitalizar contenido, sino de garantizar que los alumnos pudieran aprender de forma activa y reflexiva en un nuevo sistema.

Al mismo tiempo, el cambio a lo digital exigía una infraestructura escalable para:

  • Crear grandes volúmenes de ejercicios rápidamente.
  • Proporcionar retroalimentación personalizada en tiempo real.
  • Apoyar a profesores con distintos niveles de competencia técnica.
  • Dar a los estudiantes herramientas para practicar de forma independiente y significativa.

Otras plataformas como Google Classroom, aunque útiles para compartir documentos, carecían de la sofisticación necesaria para una evaluación matemática profunda y retroalimentación formativa.

La solución

Fue entonces cuando WirisQuizzes entró en escena: no solo como un complemento, sino como el motor central detrás de la plataforma personalizada de matemáticas de La Salle.

Liderados por Javier y el profesor de matemáticas Guillermo Pérez González, el departamento comenzó a construir un banco compartido de ejercicios directamente en Moodle usando WirisQuizzes. No eran simples preguntas: eran ejercicios dinámicos e inteligentes capaces de ofrecer retroalimentación paso a paso, reconocer la comprensión parcial y regenerarse con diferentes datos para una práctica ilimitada.

“Descubrimos el verdadero poder de WirisQuizzes cuando nos dimos cuenta de que podíamos dividir un problema en partes”, dijo Javier. “No se trata solo de obtener la respuesta final. Si un alumno acierta el 20% inicial, la plataforma lo reconoce y lo puntúa”.

WirisQuizzes se convirtió en mucho más que una herramienta de evaluación: pasó a ser el asistente personal de estudio de los estudiantes. “Ahora nos preguntan: ‘¿Hay un quiz de este tema?’”, compartió Guillermo. “Se ha convertido en una parte natural de cómo estudian y se preparan”.

El proceso de implementación

Evaluación

La transición comenzó hace casi una década, cuando La Salle eliminó los libros impresos en algunos niveles de matemáticas. Con un modelo digital en el horizonte, Javier comenzó a explorar alternativas.

“Encontré WirisQuizzes en internet por casualidad”, dijo. “Y después de probar sus capacidades, lo propuse a mis
compañeros. A partir de ahí, despegó”.

Customization

Con el banco de preguntas de Moodle a nivel institucional, los docentes crearon cientos de preguntas organizadas por temas: polinomios, funciones, geometría, probabilidad y más. Cada una incluía retroalimentación personalizada.

“Casi todas nuestras preguntas muestran el proceso de solución”, explicó Javier. “Esto hace que los estudiantes aprendan de forma independiente; incluso sus padres pueden seguir el razonamiento”.

El trabajo fue colaborativo. Los profesores construyeron y reutilizaron el contenido de otros.

“Nunca asignamos categorías formalmente”, contó Guillermo. “Si alguien tenía tiempo libre, se sumaba y añadía al banco. Es un recurso compartido para todos”.

Despliegue

WirisQuizzes se desplegó a través de Moodle en toda la escuela. Los profesores podían:

  • • Seleccionar preguntas de un banco compartido.
    • Crear quizzes rápidamente.
    • Ofrecer evaluaciones cronometradas o ejercicios de práctica.
    • Usar quizzes para clase, deberes o incluso durante horas de sustitución.

El colegio también exportó bancos de preguntas a otros campus de La Salle en Tenerife, Madrid y Gran Canaria. La adopción varió según el soporte técnico y la formación de cada centro, pero el sistema estaba diseñado para facilitar la exportación/importación.

Formación

Aunque muchos usuarios principales eran docentes de matemáticas o STEM con experiencia en programación, otros se sintieron intimidados por el concepto. “Algunos escuchan ‘programación’ y piensan en C++”, bromeó Guillermo. “Pero no es así. Si dieran un paso, verían lo sencillo que es”.

Para abordar esta situación, La Salle y Wiris planearon sesiones de formación adaptadas que comienzan de forma simple, centrándose en lo básico de la creación de quizzes antes de avanzar a lógica y scripting más complejos.

Los resultados

La plataforma de aprendizaje matemático de La Salle, impulsada por WirisQuizzes, ha logrado resultados transformadores en varios aspectos.

Mayor autonomía y motivación estudiantil

Los estudiantes comenzaron a solicitar voluntariamente quizzes para practicar nuevos temas. “Es como tener un tutor personal”, dijo Javier. En un caso memorable, se conectó un fin de semana y encontró a nueve estudiantes que ya habían completado un quiz de práctica con una puntuación perfecta. “Competían de forma sana. Se volvió divertido”.

Eficiencia colaborativa entre docentes

El departamento de matemáticas creó un banco de más de 600–700 preguntas reutilizables en diferentes cursos y asignaturas. Esto redujo significativamente el tiempo de preparación y aumentó la calidad y la consistencia de las preguntas.

Participación y transparencia para las familias

Como los quizzes incluían retroalimentación, los padres podían seguir el proceso incluso sin tener conocimientos
sólidos de matemáticas.

“Algunos nos dijeron que estaban encantados de ver a sus hijos trabajar de forma autónoma”, compartió
Guillermo.

Evaluación formativa a gran escala

Los profesores utilizaron quizzes para diagnosticar el progreso semanal de los alumnos. “En Bachillerato, puedo lanzar tres quizzes por semana, y todos cuentan para la nota”, explicó Guillermo. “Eso mantiene a todos trabajando de manera constante”.

“WirisQuizzes no es solo un motor de quizzes”, añadió Javier. “Es un sistema completo de retroalimentación. Es la columna vertebral de nuestra plataforma de matemáticas”.

El futuro de WirisQuizzes en La Salle

La Salle continúa ampliando el uso de WirisQuizzes más allá de las matemáticas:

  • Han desarrollado preguntas para economía, tecnología e incluso geografía.
  • Algunos docentes exploran cómo la retroalimentación con IA podría ofrecer rutas personalizadas de refuerzo.
  • Cada vez más profesores de la red de La Salle participan en próximas formaciones para aprender a crear preguntas y personalizar retroalimentación.

También han mostrado interés en explorar la supervisión remota, la integración con otras plataformas LMS como Google Classroom y la creación de contenido conjunto con otros centros.

Conclusión

La transformación de La Salle es un ejemplo brillante de cómo una escuela puede construir su propia plataforma de aprendizaje de matemáticas colaborativa, inteligente y escalable.

Al integrar WirisQuizzes en todos los niveles de la enseñanza —desde el aula hasta el estudio en casa— los profesores empoderaron a los estudiantes con autonomía, a los padres con transparencia y a la escuela con estrategias de enseñanza basadas en datos.

Lo que comenzó como el experimento de un profesor se ha convertido en una iniciativa a nivel institucional que está cambiando la forma en que La Salle enseña y los estudiantes aprenden.

👉 ¿Quieres construir tu propia plataforma de matemáticas impulsada por la retroalimentación?

Ponte en contacto hoy mismo

Hacer el trabajo de la gente en STEM más significativo