Año: 2025

Categorías
Sin categorizar

IA para matemáticas: la forma inteligente de crear cuestionarios más rápido

Crear cuestionarios de matemáticas atractivos y variados puede ser una tarea sorprendentemente laboriosa. Los profesores a menudo se enfrentan a la temida página en blanco, luchando por idear problemas nuevos que se adapten a los diferentes niveles, temas y necesidades de los alumnos. Pero eso está a punto de cambiar. Con la llegada de la IA para matemáticas a las aulas, la creación de cuestionarios acaba de recibir una potente mejora.

Conoce LearningLemur: tu generador de preguntas con IA

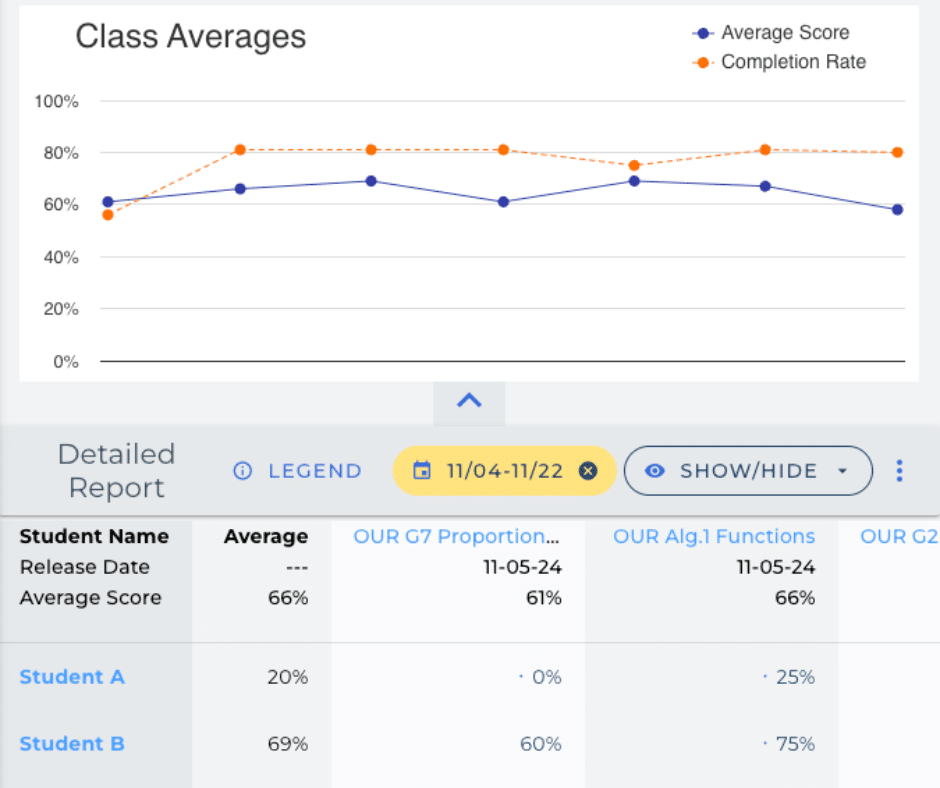
LearningLemur es una plataforma matemática intuitiva integrada con Google Classroom que ofrece cuestionarios personalizables, calificación automática y comentarios personalizados, lo que ahorra tiempo a los educadores y mejora el aprendizaje de los alumnos. Su amplia biblioteca de cuestionarios y ejercicios personalizables fomenta el compromiso y el dominio, mientras que los análisis detallados ayudan a los educadores a realizar un seguimiento del progreso e identificar las áreas de mejora. Desde la simplificación de la creación de tareas hasta la entrega de comentarios instantáneos, LearningLemur transforma las aulas en espacios de aprendizaje dinámicos e interactivos, haciendo que las matemáticas sean más accesibles y atractivas para todos los estudiantes.

Ahora, Wiris ha introducido una nueva función en LearningLemur: un generador de preguntas matemáticas que entiende tus necesidades y genera cuestionarios listos para usar en segundos. Está diseñado para abordar uno de los puntos débiles más comunes de los educadores: cómo empezar a crear evaluaciones matemáticas de forma eficiente sin sacrificar la calidad.

Esto es lo que ofrece la nueva herramienta de LearningLemur basada en inteligencia artificial:

  • Describe el tipo de preguntas que deseas.
  • Recibe al instante un conjunto de problemas matemáticos personalizados.
  • Edítalos, perfecciónalos y asígnelos directamente a tus alumnos.

Olvídate de empezar desde cero. Esta herramienta te ayuda a trabajar de forma más inteligente, no más dura, todo ello dentro de una plataforma intuitiva y fácil de navegar, incluso para profesores con experiencia tecnológica limitada.

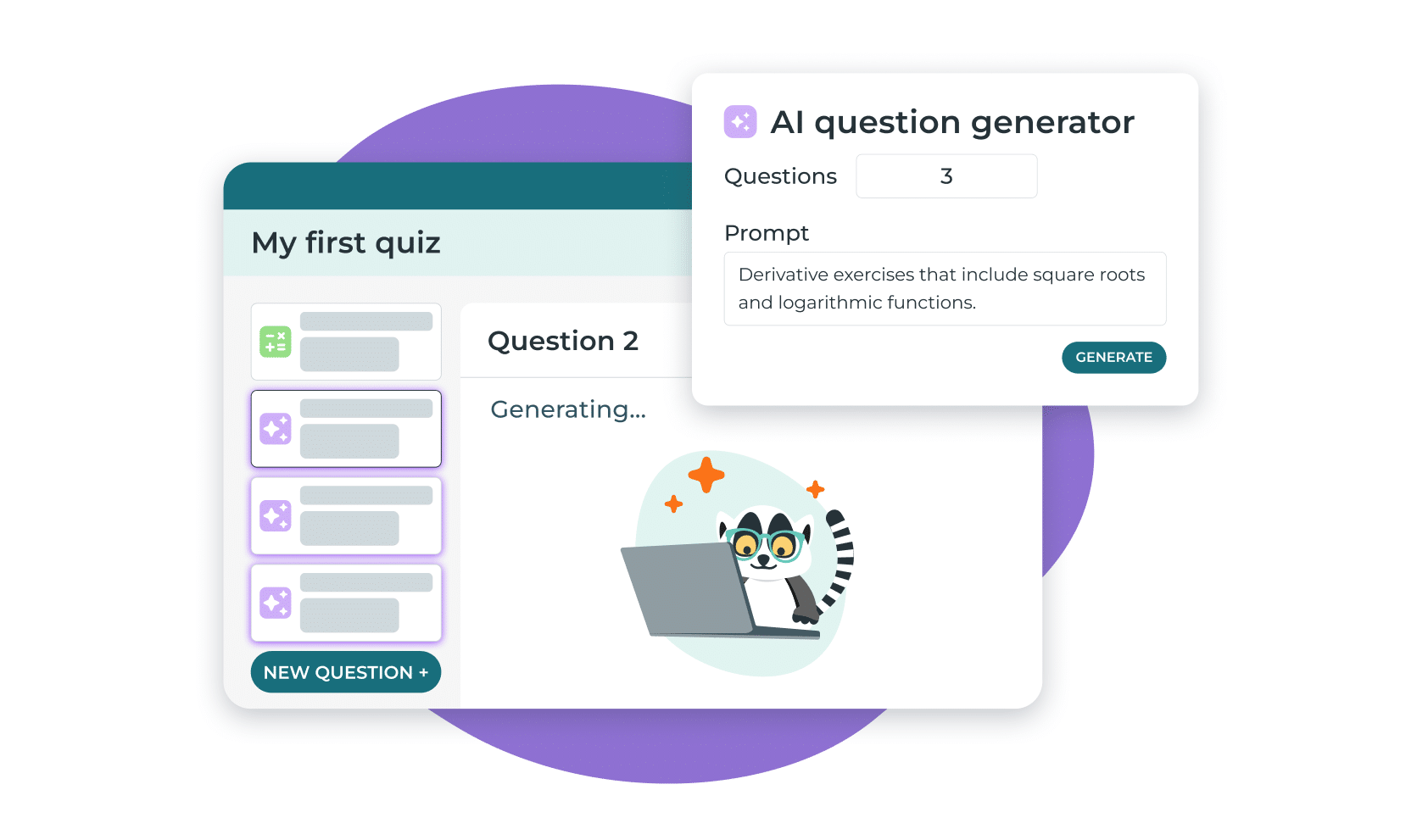
¿Cómo funciona?

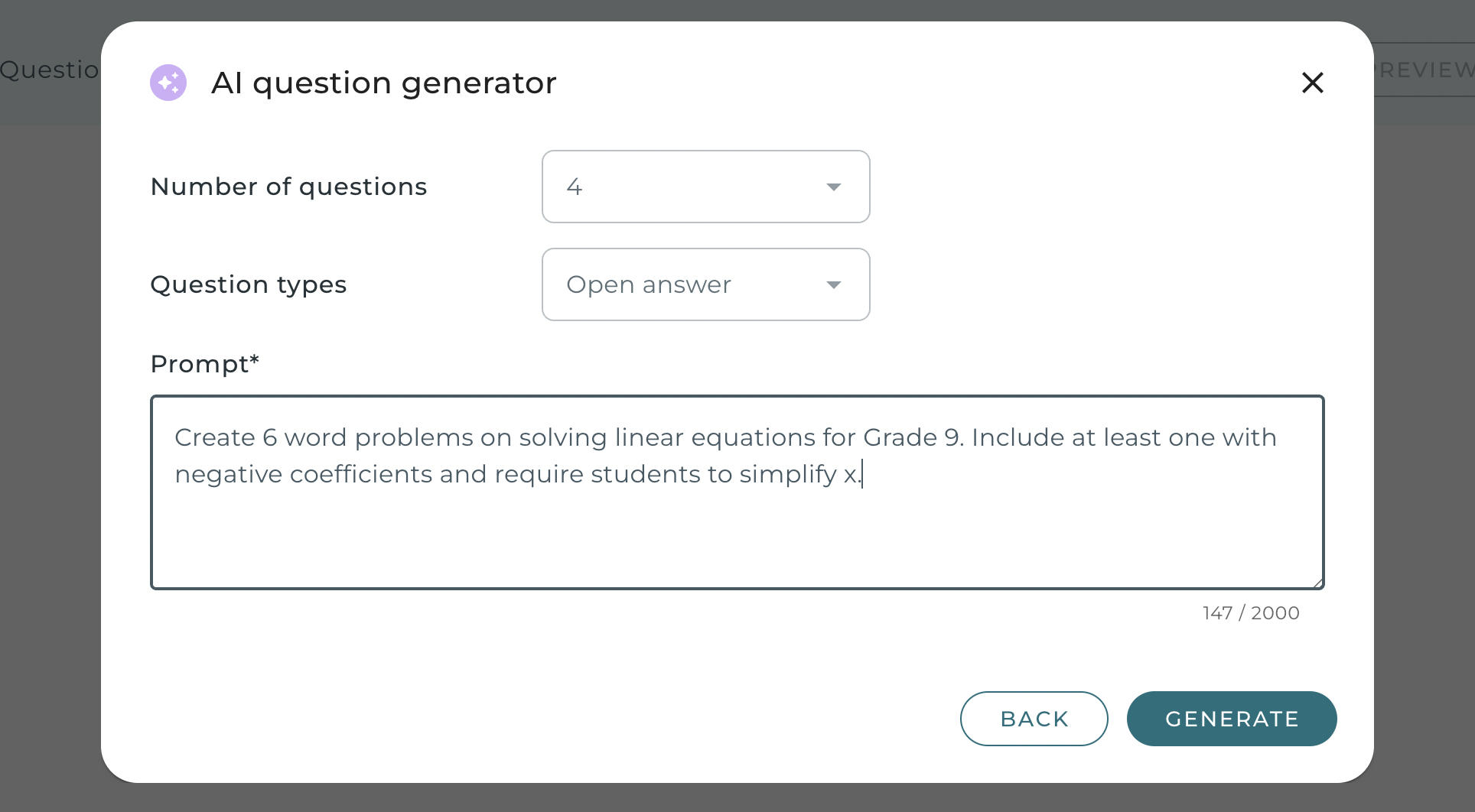
El uso de esta herramienta es sencillo y directo. Los profesores introducen el número de preguntas, seleccionan el tipo de pregunta (por ejemplo, respuesta abierta, opción múltiple) y, por último, proporcionan una indicación (por ejemplo, «Crea problemas de suma de fracciones para alumnos de 12.º curso. Pídeles que los simplifiquen»).

La IA se encarga del resto, ofreciendo un borrador de contenido que se ajusta a tus instrucciones. Y como está impulsado por el fiable motor de corrección de Wiris, usted mantiene plena confianza en la precisión matemática.

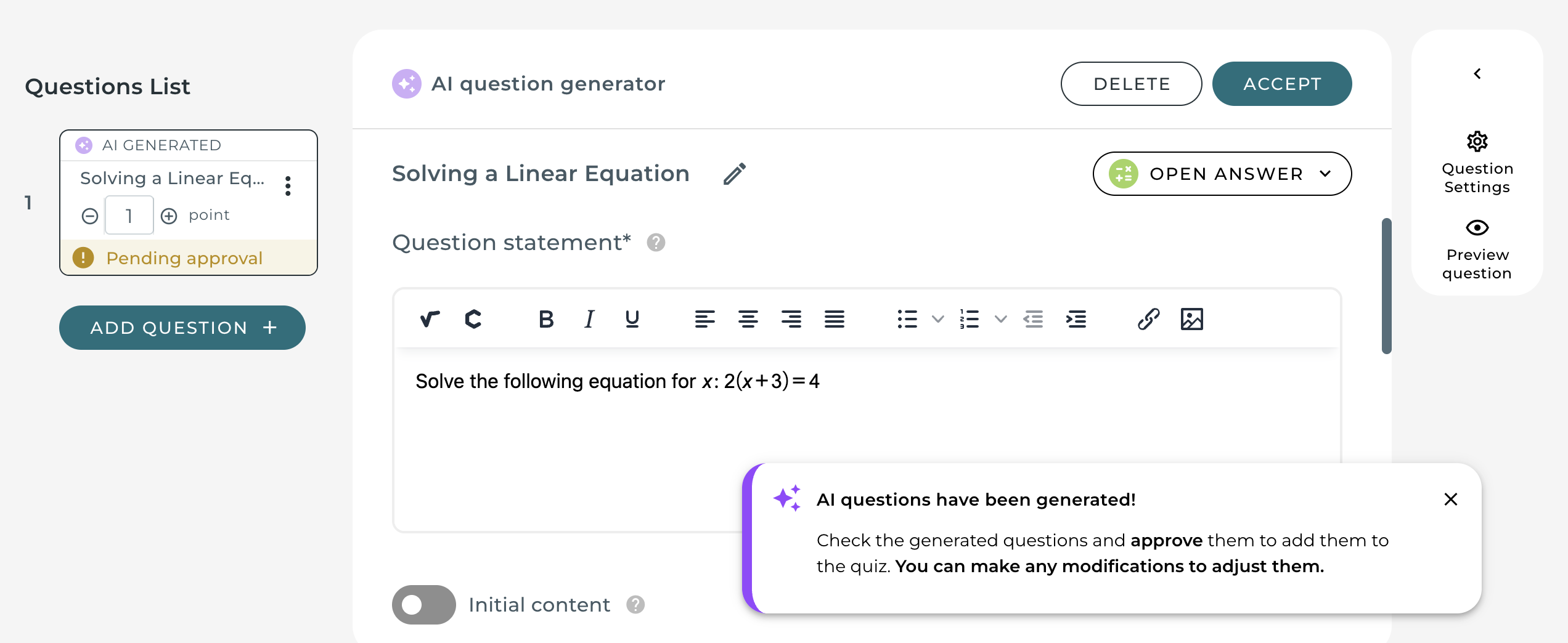
Ai generated question maths

Por qué esta función de IA es importante para los educadores

El generador de preguntas de IA LearningLemur no solo sirve para ahorrar tiempo. Está diseñado para ayudar a los profesores a centrarse en lo que realmente importa: la pedagogía, la claridad y la alineación con el plan de estudios. Mientras la IA se encarga de la generación, los profesores pueden dar forma al resultado garantizando la alineación pedagógica con los objetivos del plan de estudios, ajustando la complejidad y el estilo de cada pregunta y refinando el lenguaje y la claridad para el grupo específico de alumnos. Esta herramienta no sustituye su experiencia, sino que acelera su flujo de trabajo, lo que le permite dedicar más tiempo a una enseñanza eficaz.

Consejos para redactar indicaciones eficaces

Redactar la indicación adecuada es fundamental para sacar el máximo partido a la herramienta de IA para matemáticas de LearningLemur. Piensa en ello como si estuvieras dando instrucciones a un compañero o delegando en un profesor en prácticas. Sé claro, sé específico e incluye lo siguiente:

  • Especifica el tema matemático exacto que quieres evaluar en tus alumnos. Por ejemplo, indica si quieres ejercicios sobre fracciones o polinomios.
  • Defina el nivel educativo o la edad de sus alumnos para adaptar la dificultad. Las preguntas deben ser accesibles pero desafiantes y deben ajustarse a los conocimientos y habilidades de sus alumnos.
  • Añada cualquier restricción. Si tiene requisitos específicos, como simplificar las respuestas o utilizar solo decimales, asegúrese de incluirlos. Esto garantiza que las preguntas generadas cumplan con sus criterios pedagógicos o de examen.
  • Opcionalmente, utilice problemas verbales para añadir contexto y generar situaciones con las que los alumnos puedan identificarse. Añadir contexto o situaciones de la vida real hace que los problemas sean más atractivos y fáciles de entender para los alumnos. Por ejemplo, enmarcar un problema en el contexto de las compras, los viajes o la ciencia ayuda a conectar las matemáticas con la vida cotidiana y aumenta la motivación.

Ejemplos de indicaciones

«Crea 6 problemas verbales sobre la resolución de ecuaciones lineales para el 9º curso. Incluya al menos uno con coeficientes negativos y pide a los alumnos que simplifiquen x».

«Crea 10 preguntas sobre la simplificación de expresiones algebraicas para alumnos de 11 años. Incluye al menos una pregunta que implique la propiedad distributiva y otra con factorización».

«Crea 5 preguntas para alumnos de primer año de matemáticas universitarias sobre el cálculo del rango de una matriz utilizando operaciones elementales con filas».

Create 6 word problems on solving AI maths

Casos de uso en el aula real

El generador de preguntas matemáticas LearningLemur se adapta a todos los niveles y contextos:

  • Para la práctica diaria, genera variaciones para reforzar un concepto.
  • Para la evaluación formativa, adapta la dificultad y el formato.
  • Para los deberes, proporciona instantáneamente conjuntos diferenciados por nivel.
  • Para la preparación de exámenes, crea bancos de preguntas por tema o habilidad.

Y como se puede editar cualquier cosa, se integra perfectamente en cualquier estilo de enseñanza.

Necesidades de aprendizaje diversas: adapta fácilmente el contenido a las necesidades de los alumnos

Desde la perspectiva de los profesores, LearningLemur ofrece una gran flexibilidad, ya que los educadores con tiempo o recursos limitados para crear problemas matemáticos ahora pueden generar contenido de alta calidad más rápidamente. Estas ventajas son especialmente evidentes para los profesores que gestionan clases numerosas, ya que pueden personalizar el contenido y reducir el tiempo de preparación.

Además, LearningLemur permite a los profesores abordar las diversas necesidades de sus alumnos mediante la creación de cuestionarios y ejercicios personalizados que se adaptan a los diferentes niveles de habilidad y requisitos de aprendizaje. Los profesores también pueden asignar tareas específicas para casa, lo que permite a los alumnos reforzar competencias concretas en las que pueden necesitar apoyo adicional.

Empoderar a los profesores a través de la automatización inteligente

La IA para las matemáticas no consiste en sustituir a los educadores, sino en empoderarlos. LearningLemur es un claro ejemplo de cómo los generadores de preguntas con IA pueden reducir la fricción en el proceso creativo, dejando el control pedagógico total en manos de los profesores.

Tanto si estás luchando contra el bloqueo del escritor como si intentas generar rápidamente varias versiones de un cuestionario, esta herramienta te ofrece una sólida ventaja inicial.Prueba ahora la IA de LearningLemur

Prueba ahora la AI de LearningLemur

Categorías
Sin categorizar

Matemáticas en la UNED: cómo Wiris revoluciona la enseñanza

university computer room

Aprender matemáticas en la UNED sin barreras: el papel de Wiris

Garantizar que el contenido matemático y científico pueda crearse, compartirse y evaluarse fácilmente supone todo un reto en el entorno digital educativo en constante evolución.

La Universidad Nacional de Educación a Distancia (UNED), el principal centro universitario de modalidad de educación a distancia en España, pronto identificó este desafío. Con miles de estudiantes de varias especialidades, esta institución buscaba una solución sólida para mejorar sus procesos de enseñanza y evaluación, en concreto de las asignaturas relacionadas con las matemáticas y las ciencias.

Con el objetivo de mejorar la experiencia de enseñar matemáticas en la UNED, la universidad apostó por las soluciones digitales de Wiris, integrando WirisQuizzes y MathType en su metodología educativa. A lo largo de más de 15 años esta universidad ha seguido confiando en las soluciones matemáticas de Wiris para respaldar sus necesidades de educación digital, que están en constante evolución. Desde Wiris nos hemos reunido con Mari Carmen García Llamas, profesora del Grado en Economía y Grado en Turismo, y Raúl Morales Hidalgo, responsable del Área Plataforma Docente de la UNED, para entender cómo estas herramientas han mejorado los métodos de evaluación y enseñanza de las matemáticas.

El reto: enseñar matemáticas en el entorno digital

Antes de incorporar las soluciones de Wiris, la UNED se enfrentaba a importantes desafíos para crear y comunicar de manera eficaz contenido matemático en entornos digitales. Desde el punto de vista técnico, el mayor desafío era integrar una herramienta de edición matemática en su plataforma de aprendizaje personalizada. Los docentes tenían dificultades para escribir fórmulas en foros, tareas y pruebas, lo que afectaba de forma negativa a la experiencia de aprendizaje de los alumnos.

Los docentes necesitaban una solución intuitiva que permitiera insertar fácilmente expresiones matemáticas en pruebas y garantizara una interacción fluida con los estudiantes.

Carmen comenta:

«Sin una herramienta con la que poder escribir símbolos matemáticos, explicar cálculos era todo un reto. Ya fuera una integral o una ecuación algebraica, resultaba muy difícil precisar dónde habían cometido errores los alumnos.»

Asimismo, la UNED necesitaba una herramienta que ayudara a la evaluación continua y que permitiese introducir expresiones matemáticas en los cuestionarios, tanto en los enunciados de los problemas como en las opciones de respuesta. La ausencia de dicha herramienta limitaba la creación de pruebas y tareas.

uned student working with WirisQuizzes on a computer

La solución: impulsar el apredizaje de matemáticas en la UNED con Wiris

Para superar estos retos, la UNED exploró las soluciones disponibles y descubrió que WirisQuizzes y MathType eran las herramientas más completas y más sencillas de integrar para satisfacer sus necesidades. Su decisión de implementar las soluciones de Wiris se basó en varios factores clave:

Integración perfecta con su plataforma Open LMS

Al principio, la UNED conoció MathType a través de recomendaciones de los docentes y se interesó especialmente por su integración con Microsoft Office. Sin embargo, como la institución ya contaba con una plataforma personalizada, necesitaba una solución que pudiera incorporarse por completo en ella.

El equipo técnico de Wiris colaboró con la UNED para implementar MathType y WirisQuizzes en la plataforma con el fin de garantizar una transición fluida y con una mayor funcionalidad.

Facilidad de uso para docentes y estudiantes

Con el apoyo de Wiris, la enseñanza de matemáticas en la UNED ganó en facilidad al permitir al profesorado escribir y editar fórmulas en foros, tareas y pruebas. Esto ayudó a eliminar las barreras a las que se enfrentaban anteriormente con respecto a la comunicación matemática entre alumnos y educadores.

Carmen destaca el avance que supuso:

«Necesitábamos una herramienta que resultase fácil de utilizar tanto para los estudiantes como para los profesores. Wiris permite crear pruebas con todo tipo de contenido matemático en las que las preguntas se pueden personalizar al máximo.»

Fomentar el aprendizaje activo rompiendo con la memorización

Una de las características más destacadas de WirisQuizzes es que permite introducir expresiones matemáticas aleatorias en pruebas. De esta forma, los alumnos reciben una versión única de los ejercicios, lo que los disuade de recurrir a la memorización y promueve un aprendizaje activo. Carmen comenta a este respecto:

«Con WirisQuizzes, podemos crear cuestionarios
con ejercicios completamente diferentes. El nivel
de flexibilidad que ofrece es excepcional.»

El valor de WirisQuizzes: mejorar la participación y la práctica del estudiante

Aunque la UNED se centró inicialmente en MathType, pronto descubrieron que WirisQuizzes ofrecía ventajas adicionales. A medida que expandían sus estrategias de evaluación digital, WirisQuizzes resultó ser una herramienta inesperada pero muy valiosa a la hora de mejorar la participación y las oportunidades de práctica de los estudiantes.

Raúl comparte con entusiasmo:

«Cuando empezamos a hacer cambios en la plataforma, WirisQuizzes nos sorprendió gratamente. Nos pareció todo un regalo con el que no contábamos y se ha convertido en un elemento fundamental.»

El proceso de implementación: un enfoque colaborativo

Para incorporar de forma efectiva las herramientas digitales de Wiris en la enseñanza de matemáticas en la UNED, la universidad y el equipo técnico de Wiris llevaron a cabo un proceso de implementación estructurado:

Comprensión de las necesidades institucionales

Los docentes y el personal técnico de la UNED colaboraron con Wiris para determinar los requerimientos específicos, sobre todo en cuanto a la necesidad de integración en la plataforma y de evaluación de contenido matemático.

Personalización e integración

Los expertos técnicos de Wiris personalizaron las herramientas para que cumplieran los requisitos de la plataforma de la UNED con el fin de garantizar una experiencia de usuario fluida. Asimismo, el equipo de Wiris ayudó a resolver las posibles dudas y proporcionó consejos y formación respecto al uso eficiente de WirisQuizzes.

Implementación en Open LMS

La integración se implementó de forma satisfactoria en Open LMS, lo que posibilitó que los profesores pudieran crear y editar fórmulas en pruebas y foros de debate fácilmente.

El resultado: Más flexibilidad en la creación y evaluación de los contenidos de matemáticas en la UNED

Tras la implementación del aprendizaje matemático online con Wiris, la UNED experimentó mejoras muy notables en la eficiencia educativa y la participación de los alumnos:

  • Mayor flexibilidad de los docentes a la hora de crear pruebas de matemáticas.
  • Mayor participación de los estudiantes a través de ejercicios aleatorios.
  • Comunicación matemática fluida en foros y tareas.
  • Rápido servicio de soporte técnico para garantizar un uso fluido ininterrumpido.

Carmen subraya:

«Wiris nos permite crear pruebas diferenciadas con diversas opciones, por lo que la autoevaluación es un proceso dinámico e interactivo.»

Los alumnos también se benefician de esta experiencia de aprendizaje dinámica e interactiva en la que cada ejercicio es único, ya que de esta forma pueden practicar con múltiples variaciones de los problemas sobre un mismo tema.

UNED apuesta por WirisQuizzes: hacia una mayor integración en la docencia digital

Tras disfrutar de las ventajas de WirisQuizzes, la UNED muestra un gran interés por ver cómo esta herramienta evoluciona y sigue respaldando sus necesidades de aprendizaje matemático online. Aunque ya se utiliza para la autoevaluación continua, los miembros del profesorado valoran sus posibilidades y seguirán integrándola en sus procesos didácticos.

Carmen afirma:

«Varios colegas me han comentado el potencial de las soluciones de Wiris. Creo que solo estamos empezando a descubrir todo lo que podemos hacer con estas herramienta.»

Conclusión: la UNED avala el aprendizaje matemático online con Wiris

Después de más de 15 años de experiencia con los productos de Wiris, la UNED recomienda sin lugar a dudas WirisQuizzes y MathType por su facilidad de uso, sus potentes funciones de evaluación y su perfecta integración.

Raúl enfatiza:

«Siempre recomiendo Wiris por lo bien que funciona la herramienta. Por eso llevamos 15 años con vosotros.»

Prueba Wiris en tu institución

El caso de éxito de la evolución de la enseñanza de matemáticas en la UNED refleja el impacto positivo de integrar soluciones como las de Wiris en la educación digital.

Si buscas mejorar la evaluación de matemáticas en tu centro y quieres que tus estudiantes y profesores puedan escribir fórmulas y expresiones fácilmente, no esperes más y ponte en contacto con nosotros hoy mismo.

Solicitar una demostración

Categorías
Sin categorizar

Enseñar matemáticas online: Transformando la educación con Wiris

benefits of studing online

La enseñanza de las matemáticas en línea está redefiniendo el panorama educativo. La aparición de herramientas digitales avanzadas ha dado a los docentes la capacidad de ofrecer experiencias de aprendizaje personalizadas y flexibles. Entre estas innovaciones, los métodos de enseñanza de matemáticas online son cruciales para mejorar la participación del alumnado, la retención del conocimiento y el rendimiento académico. Este artículo explora estas estrategias transformadoras y destaca cómo Wiris permite a los educadores implementar las herramientas efectivo y eficientemente.

Tendencias clave en la enseñanza de matemáticas online: personalización, implicación y flexibilidad como prioridades

En un panorama educativo cada vez más digital y dinámico, las estrategias modernas de enseñanza de matemáticas en línea evolucionan para atender la diversidad del alumnado actual. El foco ya no está solo en impartir contenido; se ha desplazado hacia la creación de entornos que fomenten la personalización, maximicen la implicación y ofrezcan flexibilidad para acomodar distintos estilos y ritmos de aprendizaje.

Las tendencias más destacadas e impactantes en la enseñanza de matemáticas online hoy incluyen:

  • Aulas invertidas: El modelo de aula invertida transforma el paradigma educativo tradicional al trasladar la instrucción directa fuera del aula —normalmente mediante vídeos, lecturas o contenidos online— y reservar el tiempo de clase para el aprendizaje activo. Este enfoque fomenta una comprensión más profunda a través de debates, resolución colaborativa de problemas y ejercicios interactivos en educación matemática. El alumnado se familiariza con el material a su propio ritmo antes de la clase y aplica su conocimiento durante las clases, ya sean online o presenciales.
  • Microaprendizaje: El microaprendizaje consiste en impartir la información en segmentos pequeños y concretos que resultan más fáciles de asimilar y retener. En lugar de abrumar con lecciones largas y complejas, divide el contenido en unidades concisas y manejables. En la enseñanza innovadora de matemáticas online, este método es altamente eficaz porque reduce la sobrecarga cognitiva y permite alcanzar el dominio un concepto a la vez.
  • Aprendizaje personalizado: El aprendizaje personalizado aprovecha la tecnología para adaptar la experiencia educativa a las necesidades, habilidades e intereses de cada estudiante. En el contexto de la enseñanza de matemáticas online, este enfoque permite a los docentes ajustar la instrucción de manera dinámica, facilitando que el alumnado progrese a su ritmo. Garantiza que cada persona reciba el nivel adecuado de apoyo y desafío, potenciando la motivación y el rendimiento académico.

Las soluciones de Wiris, incluidas WirisQuizzes y LearningLemur, representan herramientas online para la enseñanza de matemáticas que operacionalizan estas metodologías, permitiendo a los educadores desarrollar evaluaciones dinámicas y rutas de aprendizaje adaptadas a sus estudiantes.

Aplicaciones en el mundo real: cómo estas estrategias de enseñanza online benefician al alumnado

Adoptar el aprendizaje personalizado, el microaprendizaje y el modelo de aula invertida dota al alumnado de competencias críticas para el éxito en el mundo real. Estas metodologías no solo impulsan los resultados académicos, sino que también desarrollan habilidades esenciales para prosperar en entornos profesionales digitales y colaborativos.

Mediante métodos innovadores de enseñanza de matemáticas en línea, los educadores fomentan el desarrollo de habilidades vitales como la resolución de problemas, el pensamiento crítico y el aprendizaje autodirigido, competencias cada vez más demandadas en las industrias STEM y en la futura fuerza laboral.

Aulas invertidas: aprender haciendo en lugar de memorizar

El modelo de aula invertida fomenta la autonomía del alumnado al trasladar la entrega de contenidos fuera del aula y reservar las sesiones presenciales o sincrónicas para actividades colaborativas de mayor nivel cognitivo. En lugar de escuchar pasivamente clases magistrales, los estudiantes trabajan con materiales preparatorios —como vídeos o lecturas— a su propio ritmo y utilizan el tiempo de clase para aplicar conceptos mediante la resolución de problemas y el debate.

Este método promueve el pensamiento crítico, la comprensión profunda y la participación activa. Asimismo, atiende a distintos estilos de aprendizaje e impulsa a los estudiantes a asumir una mayor responsabilidad sobre su progreso. Al convertir el aula en un entorno dinámico e interactivo, el modelo invertido refuerza competencias clave como la comunicación, la colaboración y el análisis.

Beneficios del modelo de aula invertida

A continuación se presentan los principales beneficios del modelo de aula invertida, un enfoque que gana cada vez más tracción en los métodos educativos modernos:

  • Asigna cuestionarios preparatorios y dinámicos para preparar al alumnado para las actividades en clase. Asignar cuestionarios de preparación garantiza que el estudiantado se implique con los conceptos clave antes de la clase. Esta preparación permite dedicar las sesiones a aplicar conocimientos en lugar de repasar fundamentos. Herramientas como WirisQuizzes y LearningLemur pueden ayudarte a desarrollar estos cuestionarios adaptados a las necesidades de tus estudiantes.
  • Fomenta entornos de aula interactivos basados en el debate. Con la exposición previa al material, el tiempo en clase puede dedicarse a discusiones y a la resolución colaborativa de problemas. Este cambio potencia el pensamiento crítico y promueve una comprensión más profunda mediante el diálogo activo.
  • Promueve la participación activa y la colaboración. Las aulas invertidas animan a los estudiantes a participar y colaborar con sus pares. El trabajo en equipo y las actividades de resolución de problemas desarrollan no solo competencias académicas, sino también habilidades esenciales como la comunicación y el trabajo en equipo.

girl studing online

El poder del microaprendizaje: lecciones breves para una mejor retención

El microaprendizaje está ganando fuerza como estrategia eficaz en la enseñanza de matemáticas online. Este método descompone conceptos complejos en unidades manejables, promoviendo una comprensión más profunda y una mejor retención a largo plazo.

Con WirisQuizzes y LearningLemur, los docentes pueden diseñar cuestionarios breves y focalizados que refuercen los conceptos fundamentales con eficiencia. Los mecanismos de retroalimentación inmediata facilitan correcciones en tiempo real. Estas microevaluaciones ejemplifican enfoques innovadores de enseñanza de matemáticas online que reducen la carga cognitiva y mejoran la eficacia del aprendizaje. Estas herramientas agilizan el microaprendizaje al permitir la creación de cuestionarios interactivos y examenes.

WirisQuizzes incorpora una funcionalidad que potencia el microaprendizaje al proporcionar retroalimentación personalizada para preguntas abiertas de matemáticas. Ofrece tres tipos principales de feedback: retroalimentación sugerente, que guía al alumnado hacia el descubrimiento autónomo; retroalimentación confirmatoria, que refuerza las respuestas correctas y la confianza; y retroalimentación correctiva, que identifica errores y aporta la solución correcta. Esta retroalimentación inmediata y adaptativa fomenta el pensamiento crítico y garantiza un aprendizaje eficiente y centrado, en perfecta consonancia con los principios del microaprendizaje.

feedback with wirisquizzes

Aprendizaje personalizado: experiencias educativas a medida

El aprendizaje personalizado es una piedra angular de las metodologías educativas modernas, especialmente en la enseñanza de matemáticas online. Se apoya en la tecnología para personalizar la experiencia educativa según las necesidades, habilidades y ritmos de aprendizaje de cada estudiante.

WirisQuizzes y LearningLemur son fundamentales para posibilitar este nivel de personalización:

  • WirisQuizzes, orientado a educación superior, permite a los docentes diseñar cuestionarios sofisticados que incorporan expresiones matemáticas, representaciones gráficas y respuestas textuales dinámicas. Sus capacidades avanzadas de aleatorización y evaluación generan pruebas únicas para cada estudiante, promoviendo la práctica mediante conjuntos de problemas variados e individualizados.
  • LearningLemur, orientado a K12 e integrado de forma fluida con Google Classroom, ofrece una plataforma completa para cuestionarios personalizables, calificación automática y retroalimentación personalizada. No solo ahorra tiempo valioso a los docentes, sino que también fomenta la implicación y el dominio por parte del alumnado. La amplia biblioteca de ejercicios adaptables y las analíticas detalladas permiten monitorizar el progreso e intervenir cuando sea necesario, potenciando aún más el aprendizaje. Además, LearningLemur ahora incorpora un generador de preguntas matemáticas con IA que entiende tus necesidades y crea cuestionarios listos para usar en segundos. Está diseñado para resolver uno de los problemas más comunes de los educadores: cómo empezar a crear evaluaciones matemáticas de manera eficiente sin sacrificar la calidad.

learning lemur ai questions

Lo que realmente diferencia las herramientas de Wiris es su capacidad para interpretar matemáticamente cualquier respuesta, aplicar lógica matemática rigurosa para personalizar la retroalimentación y definir variables aleatorias mediante algoritmos avanzados. Estas capacidades permiten ofrecer experiencias de aprendizaje más precisas y receptivas, asegurando que cada estudiante progrese a su ritmo óptimo y reciba el apoyo adecuado a su trayectoria.

Al integrar estas soluciones, los educadores pueden crear entornos de aprendizaje adaptativos en los que la tecnología se ajusta dinámicamente a las necesidades del alumnado, proporciona retroalimentación instantánea y alinea de manera continua el contenido con los objetivos individuales de aprendizaje.

Abrazar el futuro de la educación con Wiris

La transformación digital de la educación exige metodologías docentes ágiles y centradas en el estudiante. Enseñar matemáticas online requiere herramientas sofisticadas, y Wiris está a la vanguardia, ofreciendo soluciones que permiten diseñar experiencias de aprendizaje personalizadas e interactivas.

Mejora tu estrategia de enseñanza en línea: comienza a usar WirisQuizzes hoy y experimenta las ventajas de las herramientas de nueva generación para enseñar matemáticas online.

 

Prueba WirisQuizzes ahora

Categorías
Sin categorizar

Fórmulas insustituibles: MathType y la excelencia editorial de Mondadori Education

mathtype mondadori

De una herramienta útil a una referencia estratégica de la compañía

Cuando Pietro Curci se incorporó a Le Monnier (una editorial italiana) a mediados de los años 90, ya buscaba formas de modernizar la producción de contenidos educativos en su empresa, especialmente la parte más compleja: la composición de fórmulas matemáticas. Como jefe del departamento gráfico, su responsabilidad era clara: garantizar calidad, coherencia y eficiencia en un entorno editorial.

Fue en aquellos años, antes de que Le Monnier fuera adquirida por el Grupo Mondadori Education (la mayor editorial de Italia) en 1999, cuando Curci descubrió MathType para Word. El editor de ecuaciones se volvió rápidamente indispensable, ofreciendo la posibilidad de producir fórmulas limpias, editables y reutilizables, algo impensable en aquel momento. El Grupo Mondadori Education opera en tres áreas principales: libros (publica obras de ficción, no ficción, infantiles, educativos y académicos); revistas (publica las principales revistas italianas en formato impreso y digital) y venta al por menor (gestiona una amplia red de librerías y ventas en línea). También opera en los ámbitos de la educación, los contenidos digitales y las licencias internacionales.

Con la transición a Mondadori Education, también se consolidó la evolución natural de MathType: de herramienta útil a estándar estratégico. Hoy, como jefe del departamento gráfico del área de Humanidades para secundaria, Curci supervisa una parte esencial del flujo editorial del grupo, y MathType sigue en el centro del proceso. Casi tres décadas después, MathType continúa siendo un pilar del flujo editorial de Mondadori Education. “Nuestra solución es usada por DeaScuola y Rizzoli Education, que forman parte del Grupo Mondadori Education”, explica Curci.

Lo que comenzó como una solución práctica para escribir ecuaciones en Word se ha convertido en algo mucho más grande. Con el tiempo, MathType se ha integrado profundamente en la forma de trabajar de Mondadori Education.

No solo lo utiliza un equipo o para una tarea, sino que da soporte a diferentes departamentos y se adapta a diversas partes del proceso de producción. Ya sea en el ámbito editorial o digital, MathType ha demostrado ser flexible y fiable, ganándose su lugar como punto de referencia común en toda la empresa.

Mathtype editor mondadori

 

Los desafíos

A mediados de los años 90, tanto Le Monnier como más tarde Mondadori Education necesitaban una herramienta fiable para producir contenidos matemáticos complejos. Curci recuerda las limitaciones de los primeros sistemas de composición, especialmente en términos de coherencia, reutilización e integración con herramientas como QuarkXPress.

“Necesitábamos algo estable que nos permitiera reutilizar contenido en diferentes ediciones y títulos”, comenta Curci. “MathType nos dio fórmulas como imágenes, y una imagen, como siempre digo, es para siempre. Fue revolucionario”.

Pero con el tiempo, los retos evolucionaron. El auge de la publicación digital, los contenidos en color y los formatos interactivos llevaron a las herramientas editoriales más allá de lo que podían soportar los flujos de trabajo en blanco y negro. Garantizar la compatibilidad con los nuevos sistemas operativos y las herramientas de maquetación modernas se convirtió en una necesidad estratégica.

Mondadori Education y Wiris: esfuerzos conjuntos para mejorar el producto

Mondadori Education adoptó MathType desde sus primeras versiones y nunca miró atrás. La compañía estandarizó su uso tanto para colaboradores internos como externos. Profesionales de maquetación, editores y autores trabajaban con el mismo editor de ecuaciones, simplificando la colaboración.

“Con el plugin instalado en nuestras plataformas, podemos extraer fórmulas sin redigitarlas. Ahorra tiempo y reduce errores, algo esencial cuando trabajas con más de 5.000 fórmulas en un libro de texto”, afirma Curci.

Cuando Curci y su equipo se encontraron con obstáculos, como problemas de reproducción del color, compatibilidad con EPS o problemas con los glifos de las fuentes, no renunciaron a MathType. En lugar de eso, colaboraron estrechamente con Wiris, aportando soluciones prácticas y conocimientos basados en su flujo de trabajo real.

La flexibilidad de MathType a la hora de exportar MathML para ediciones digitales, al tiempo que mantiene fórmulas basadas en imágenes de alta calidad para impresión, permitió a Mondadori Education satisfacer las demandas cambiantes sin tener que reconstruir su biblioteca de contenidos desde cero. Como afirma Curci, «gracias al MathML integrado, podemos exportar fácilmente las fórmulas como código y reutilizarlas en formatos digitales».

mathtype for indesign

El proceso de implementación

The implementation of MathType at Mondadori Education was the result of a clear vision: to establish a unified, efficient workflow for mathematical content creation. Once MathType proved to be a reliable solution, it was adopted as the official standard across the organization. This meant that all external vendors producing math formula typesetting layouts were also required to work with the same tool, fostering consistency and compatibility across every stage of production.

One of the key advantages of MathType was its ability to generate formulas as images, allowing for the long-term reuse of content. Thanks to this, legacy materials could be updated by simply adjusting style preferences, eliminating the need to recreate thousands of formulas from scratch.

The integration of MathType enabled seamless collaboration. Editorial teams received manuscripts with embedded formulas and passed them on to layout professionals, who could extract and edit the formulas directly, greatly reducing manual intervention and improving version control.

Throughout this process, Pietro Curci played a crucial role in bridging the gap between user needs and technical development. His collaboration with Wiris led to the resolution of various challenges, such as color rendering issues in EPS files, overprint settings in InDesign, and glyph compatibility. These contributions helped shape subsequent versions of the equation editor and ensured its alignment with real-world editorial demands.

Why MathType Is Essential to Mondadori Education’s Editorial Excellence

Over the years, MathType has established itself as a trusted and indispensable tool within Mondadori Education’s editorial ecosystem. Its ease of use, compatibility across platforms, and ability to generate both print and digital outputs have made it a core component of the company’s workflow. The following key benefits highlight why MathType continues to play a strategic role in ensuring quality, efficiency, and long-term content reuse at Mondadori Education.

  • Preserved editorial legacy. «MathType is irreplaceable,» says Curci. «Without it, we would have lost a huge amount of content or had to reinvest in recreating everything».
  • Increased efficiency. Automated extraction of formulas from documents, coupled with standardized workflows, greatly reduced manual effort and error rates across the team.
  • Ease of use. The platform requires no advanced technical skills, making it accessible to a broad range of professionals. «The fact that it has a simple interface doesn’t mean it’s not good. Otherwise: with just a few clicks, you understand what to do to save and typeset formulas», affirms Curci.
  • Flexibility and reusability. Formulas can be adapted to new design preferences with minimal effort, reducing rework.
  • Support for digital formats. Built-in MathML export facilitates the production of reflowable, accessible digital textbooks.
  • Collaborative customer service. The collaboration with Wiris has enabled Mondadori Education to resolve technical challenges like spot color management, overprinting, and font compatibility, ensuring consistent output across print and digital.
  • Cross-department adoption. MathType is used not only by in-house editorial teams but also by all external layout professionals who contribute to Mondadori Education’s math formula typesetting publications. Its status as a shared standard enables a smooth production chain.
  • Future-proofing. Despite working with older machines to maintain compatibility, Curci and his team are eagerly awaiting the new MathType release. The goal: support newer systems while maintaining continuity.

Looking Ahead Together

We’re entering a new era of innovation, driven by the evolution of our products and the needs of the STEM community. At Wiris, we’re actively working on meaningful improvements of MathType to better support today’s editorial and educational challenges. And we’re not doing it alone, as Mondadori Education and Pietro Curci continue to be by our side, offering their insight, testing new features, and helping us shape what’s next.

For Curci, it’s not just about modernization, it’s about continuity: «I’m not looking for glory» he says. «What I care about is sharing knowledge and ensuring that future generations can build on what we’ve created. Experience is meant to be passed on, not buried».

Mondadori Education’s relationship with MathType is not just about software: it’s about editorial integrity, long-term thinking, and the power of collaboration. «I’ve worked closely with Wiris for years. I’ve seen how they listen. This isn’t just about Mondadori Education: it’s about keeping a shared legacy alive across the publishing world». «If one day we had to stop using MathType, it would be a significant loss». 

Interested in MathType? Get in touch.

Categorías
Sin categorizar

Comprendiendo el poder del número e: el héroe oculto de las matemáticas

euler number visualization

Cuando se habla de constantes matemáticas fundamentales, π suele acaparar la atención. Sin embargo, hay otro número, igualmente vital aunque menos celebrado: el número e de Euler. Conocido simplemente como e, esta constante aparece en innumerables contextos matemáticos y aplicaciones prácticas. En este artículo exploraremos el origen, las propiedades y las aplicaciones de e, posicionándolo como una herramienta indispensable en el mundo de las matemáticas, la ciencia y las finanzas.

¿Qué es el número e de Euler?

El número e de Euler es un número irracional y trascendental, aproximadamente igual a 2.71828. Sirve como base de los logaritmos naturales y surge de manera natural en diversos procesos de crecimiento y en cálculos de límites.

El origen de e: un ejemplo práctico

Consideremos el siguiente escenario real: imagina un banco que ofrece una tasa de interés anual del 100% sobre una inversión principal de 1 €. Si el interés se capitaliza una vez al final del año, tendrás 2 €. Sin embargo, si el banco capitaliza intereses semestralmente al 50% cada seis meses, el cálculo cambia:

  • Tras seis meses: 1€ × 1.5 = 1.5€
  • Tras otros seis meses: 1.5€ × 1.5 = 2.25€

Ahora, dividamos el año en tres periodos de cuatro meses cada uno, aplicando una tasa del 33.33% cada cuatro meses:

  • Tras cuatro meses: 1€ × 1.33 = 1.3333€
  • Tras ocho meses: 1.3333€ × 1.3333 ≈ 1.7777€
  • Tras doce meses: 1.7777€ × 1.3333 ≈ 2.3703€

Entonces, si recibes pagos infinitos, ¿tendrás dinero infinito? Lamentablemente, la respuesta es no. A medida que la frecuencia aumenta —de trimestral a mensual, diaria y más allá— el monto final se aproxima a un límite. La fórmula para calcularlo es:

mathtype formula Imagen creada com MathType

Cuando n tiende a infinito, el valor converge a e. Este ejemplo simple pero poderoso demuestra la aparición natural de e en el crecimiento exponencial, explicando su papel fundamental en los modelos de interés compuesto continuo.

Propiedades fundamentales del número e

  • Irracionalidad: e no puede expresarse como una fracción simple.
  • Trascendencia: e no es raíz de ningún polinomio no nulo con coeficientes racionales.
  • Serie infinita: e puede representarse como la suma de la serie infinita. equation with mathtype

Image created with Wiris’ MathType

  • Base del logaritmo natural: la función logaritmo natural utiliza e como base, siendo integral en el cálculo y en modelos de crecimiento natural.
  • Identidad de Euler: considerada una de las ecuaciones más bellas de las matemáticas:

eiπ + 1 = 0

Esta ecuación conecta elegantemente cinco constantes fundamentales: 0, 1, e, i, y π.

Aplicaciones en distintas disciplinas

El número e de Euler no es solo una constante fundamental en matemáticas puras, también desempeña un papel central en múltiples aplicaciones prácticas en diversos campos científicos y tecnológicos. Desde modelar procesos de crecimiento hasta la gestión de riesgos, e es indispensable para comprender y predecir fenómenos complejos.

En Matemáticas

  • Cálculo: el número e es central en el cálculo, particularmente en el contexto del crecimiento y el decaimiento exponencial. Una de las propiedades más importantes de e es que la derivada de la función ex es ex en sí misma. Esta propiedad única lo hace extremadamente útil en la resolución de ecuaciones diferenciales que describen sistemas dinámicos, como el crecimiento poblacional, la desintegración radiactiva y la transferencia de calor. Simplifica el análisis de estos sistemas porque la función se replica bajo diferenciación.
  • Números complejos: la fórmula de Euler, eix = cos(x) + isin(x), es una de las ecuaciones más profundas de las matemáticas, vinculando las funciones exponenciales con las trigonométricas. Esta relación es crucial en campos como la ingeniería eléctrica y el procesamiento de señales, donde simplifica el análisis de sistemas y ondas oscilantes. Permite una comprensión más intuitiva de rotaciones y oscilaciones en el plano complejo.

En Física

  • Desintegración radiactiva: el proceso de desintegración radiactiva sigue una ley exponencial, que puede modelarse usando e. La cantidad de sustancia radiactiva restante después de un periodo se da mediante la ecuación N(t) = N0eλt, donde N(t) es la cantidad en el tiempo t, N0 la cantidad inicial y λ la constante de desintegración. Este modelo se utiliza en medicina (radiología), arqueología (datación por carbono) y física nuclear.
  • Termodinámica: en termodinámica, el factor de Boltzmann es esencial para determinar la probabilidad de que un sistema esté en un estado de energía particular. La relación exponencial que incluye e es vital para comprender sistemas en equilibrio, como la distribución de partículas en gases o el comportamiento de moléculas en procesos biológicos.

En Economía y Finanzas

  • Interés compuesto continuo: uno de los usos más comunes de e es en el cálculo del interés compuesto continuo. Si los intereses se capitalizan continuamente, la fórmula para el valor acumulado es A = Pert, donde P es la inversión inicial, r la tasa de interés y t el tiempo en años. Esto es fundamental para entender el crecimiento a largo plazo de inversiones y ahorros.
  • Modelos de riesgo: modelos financieros como Black-Scholes para la valoración de opciones dependen en gran medida de e para representar la naturaleza estocástica de los precios de los activos. e también juega un papel clave en modelos de riesgo como el cálculo de Value at Risk (VaR), que ayuda a cuantificar la probabilidad de pérdidas extremas en carteras de inversión.

En Tecnología

  • Algoritmos: e se utiliza en análisis algorítmico, particularmente al analizar el rendimiento de algoritmos que muestran crecimiento exponencial. Procesos aleatorios y algoritmos como QuickSort implican e en sus tiempos de ejecución esperados.
  • Aprendizaje automático y ciencia de datos: en machine learning, e aparece en algoritmos que modelan procesos de crecimiento o en algoritmos de optimización que ajustan parámetros con decaimiento exponencial. Por ejemplo, en el descenso de gradiente, las tasas de aprendizaje pueden decrecer exponencialmente basadas en e para optimizar el rendimiento.

En Biología y Medicina

  • Crecimiento poblacional: uno de los usos más conocidos de e es en el modelado del crecimiento poblacional. En condiciones ideales, la población sigue una curva exponencial, que se modela mediante la ecuación P(t) = P0ert, donde 𝑃(𝑡) es la población en el momento 𝑡, P0 es la población inicial y 𝑟 es la tasa de crecimiento. Este principio también es relevante en epidemiología paraentender la propagación de enfermedades.
  • Farmacocinética: el modelo de decaimiento exponencial también se usa e farmacocinética, que estudia cómo los fármacos se absorben, distribuyen, metabolizan y eliminan. La concentración de un medicamento en sangre a lo largo del tiempo suele seguir una curva de decaimiento exponencial, gobernada por e. Esto ayuda a determinar pautas de dosificación que aseguren niveles terapéuticos sin toxicidad.

Visualizando el número e con herramientas digitales de Wiris

A medida que avanzan las soluciones digitales, herramientas como MathType y CalcMe permiten trabajar fácilmente con e y otras expresiones matemáticas complejas. Ya seas investigador, docente o profesional, integrar estas tecnologías de Wiris en tu flujo de trabajo garantiza precisión y eficiencia.

Por ejemplo, para profundizar en el comportamiento de e, se puede visualizar la expresión límite  equation editor usando herramientas de graficación como CalcMe, un sistema de álgebra computacional (CAS) que permite cálculos complejos de forma rápida e intuitiva. Al aumentar x, la gráfica se aproxima al valor de e, ofreciendo una demostración visual intuitiva de este límite matemático.

Además, MathType, el editor de ecuaciones líder en el mundo que permite escribir notación matemática tan fácilmente como texto, facilita la inserción de expresiones complejas en documentos y contenido web, garantizando claridad y precisión.

number e graphic

Gráfico que muestra la función (1+1/x)x en rojo, acercándose al valor de e en azul.

Ideal para estudiantes, docentes, editores y redactores técnicos, MathType agiliza la creación de contenido científico y técnico de alta calidad en múltiples plataformas.

Para manejar de forma fluida expresiones matemáticas y visualizaciones, considera incorporar tanto MathType como CalcMe en tu conjunto de herramientas digitales. ¡Escribe aquí tus ecuaciones con el número e!

Write your e number equations here!

Categorías
Sin categorizar

De la educación a la ingeniería: por qué importa la escritura matemática eficiente

equation editor

En el mundo actual, impulsado por los datos, el contenido matemático se ha convertido en un activo clave para la innovación, la comunicación y la toma de decisiones. Ya sea diseñando algoritmos, explicando un modelo financiero o creando materiales educativos, la escritura matemática desempeña un papel fundamental al convertir ideas complejas en información útil.

Crear contenido matemático preciso, claro y accesible ya no es una tarea limitada a la academia: es una necesidad para los sectores que dependen de la precisión y la transferencia de conocimiento.

Dónde importa más la creación de contenido matemático

Numerosas industrias y ámbitos del conocimiento dependen de la capacidad de producir, adaptar y distribuir contenido matemático de alta calidad:

Educación y EdTech

En el ecosistema educativo, la creación de contenido matemático es fundamental para la experiencia de aprendizaje. Docentes, diseñadores de currículos, desarrolladores de EdTech y diseñadores instruccionales dependen de una escritura matemática precisa para preparar planes de clase, evaluaciones y recursos digitales interactivos. Desde la educación primaria hasta los cursos universitarios avanzados, la claridad de las expresiones matemáticas puede impactar directamente en la comprensión y el rendimiento del alumnado.

Además, en las plataformas EdTech, el desafío no es solo pedagógico sino también tecnológico: las ecuaciones deben ser compatibles con múltiples dispositivos, formatos y sistemas de gestión del aprendizaje (LMS). Un editor matemático eficiente permite a los educadores crear, editar y compartir contenido que mantiene su estructura y significado en distintas plataformas. En este contexto, las herramientas sólidas de creación de contenido matemático son esenciales para promover la equidad, la consistencia y la accesibilidad en la educación moderna.

mathtype editor
Ejemplo de fórmula matemática escrita con MathType de Wiris.

Comunicación científica e investigación

La investigación en campos como la física, la química, la biología y las matemáticas depende de una escritura matemática formalizada y estructurada para presentar hipótesis, validar resultados y comunicar hallazgos. Desde revistas revisadas por pares hasta preprints y solicitudes de financiación, la presentación del contenido matemático influye no solo en la comprensión, sino también en la credibilidad y profesionalidad percibidas del trabajo.

En la comunicación científica, la reproducibilidad es clave, y empieza con una notación clara y precisa. Un editor matemático potente permite a los investigadores dar formato a expresiones complejas con facilidad, ya sea escribiendo en LaTeX o usando interfaces WYSIWYG. Además, la capacidad de producir contenido matemático accesible y bien estructurado facilita la difusión más amplia y la colaboración interdisciplinaria, permitiendo que los científicos lleguen a audiencias más allá de su campo inmediato.

Ingeniería y campos técnicos

Los ingenieros y profesionales técnicos trabajan a diario con modelos, fórmulas y simulaciones complejas. Ya sea en ingeniería civil, mecánica, eléctrica o de software, la escritura matemática es central para documentar cálculos, diseñar sistemas y validar resultados. Un pequeño error en la notación puede llevar a malentendidos o consecuencias costosas en el diseño y la implementación.

Crear contenido matemático de alta calidad en este contexto requiere precisión, estandarización y compatibilidad con las herramientas de documentación técnica. Un editor matemático avanzado permite presentar fórmulas con claridad, integrarlas en documentación CAD o especificaciones y asegurar que la lógica matemática detrás de un proyecto sea transparente y reproducible. En entornos de ingeniería colaborativa, la claridad del contenido matemático ayuda a evitar ambigüedades y agiliza los procesos de revisión y aprobación.

equation editor

Economía y finanzas

En la economía y el análisis financiero, las matemáticas son el lenguaje de la lógica y la predicción. Economistas, analistas y consultores deben construir modelos, definir fórmulas y realizar cálculos complejos que sustentan informes, previsiones y decisiones estratégicas. La credibilidad de estos resultados depende no solo de los números, sino también de la claridad con la que se comunica la metodología subyacente.

La escritura matemática efectiva es crucial para garantizar que las partes interesadas —ya sean clientes, reguladores o equipos internos— comprendan y confíen en el contenido presentado. Un editor matemático profesional facilita la creación de ecuaciones coherentes y listas para publicación que pueden integrarse en informes, paneles de control o publicaciones académicas. Al invertir en mejores prácticas de contenido matemático, las instituciones financieras y los centros de análisis pueden mejorar la transparencia e impulsar decisiones basadas en datos.

Innovación corporativa y equipos de datos

En los entornos corporativos, especialmente en innovación, I+D y equipos de ciencia de datos, el contenido matemático es esencial para documentar algoritmos, modelos y marcos analíticos. Estos equipos suelen trabajar de forma transversal con gestores de producto, desarrolladores y responsables de la toma de decisiones, lo que hace esencial expresar la lógica compleja en un formato técnicamente correcto y fácilmente interpretable.

Ya sean fórmulas de aprendizaje automático, modelos operativos o estrategias de optimización, la escritura matemática profesional mejora la comunicación interna y la documentación de proyectos. Un editor matemático fiable ayuda a estandarizar la forma en que se presenta el razonamiento matemático en equipos y documentos, acelerando la incorporación, el cumplimiento y la planificación estratégica. A medida que las empresas dependen cada vez más de metodologías basadas en datos, el contenido matemático estructurado se convierte en una ventaja competitiva.

El valor de una escritura matemática clara y coherente

La escritura matemática de alta calidad abre la puerta a ventajas estratégicas significativas para cualquier organización. Cuando el contenido matemático es claro, accesible y está bien formateado:

  • Los datos técnicos se interpretan correctamente, lo que permite tomar decisiones informadas en equipos y con las partes interesadas.
  • La investigación y el análisis se comunican de forma clara, aumentando la difusión, la credibilidad y el compromiso con audiencias diversas.
  • La eficiencia mejora, ya que el contenido matemático bien formateado reduce la necesidad de correcciones y reelaboraciones.
  • La colaboración transversal se facilita, ya que el contenido estandarizado mejora la comprensión entre departamentos, instituciones o socios internacionales.

Al priorizar un contenido matemático estructurado y coherente, las organizaciones se posicionan para tener éxito en la educación, la investigación, el desarrollo y más allá.

MathType: un editor matemático diseñado para las necesidades actuales

Una vez reconocemos el valor estratégico del contenido matemático, el siguiente paso es elegir la herramienta adecuada que lo respalde. MathType es el editor de ecuaciones líder en el mundo que permite escribir notación matemática tan fácilmente como se escribe texto. Con la confianza de educadores, investigadores y profesionales en todo el mundo, es utilizado por estudiantes y docentes de K12 y universidades de disciplinas STEM.

Estas son las razones:

  • Experiencia fluida de escritura matemática. MathType permite escribir ecuaciones de forma tan intuitiva como el texto normal. Ya sea con teclado, ratón o lápiz óptico, se adapta a tu flujo de trabajo.
  • Más de 500 símbolos y estructuras matemáticas. MathType ofrece una amplia biblioteca de símbolos que cubren aritmética, álgebra, cálculo, lógica y más. Esto permite expresar con precisión incluso los conceptos más complejos, evitando improvisaciones o soluciones que comprometan la claridad.
  • Reconocimiento de escritura manual potenciado por IA. Los usuarios pueden escribir a mano ecuaciones con un lápiz óptico o una pantalla táctil, y MathType las convierte al instante en expresiones matemáticas digitales. Esto acelera la escritura y tiende un puente entre la toma de apuntes tradicional y la edición digital.
  • Exportación en formatos de alta calidad: SVG, PNG, PDF. MathType genera ecuaciones visualmente limpias que pueden exportarse en múltiples formatos. Ya sea para web, impresión o presentaciones, la calidad se mantiene intacta, lo que asegura la consistencia en todas las plataformas.
  • Salidas compatibles con accesibilidad. El editor garantiza que todas las expresiones matemáticas cumplan con los estándares de accesibilidad, compatibles con lectores de pantalla y comunicación inclusiva. Esto es crucial para instituciones educativas y proyectos del sector público con requisitos de accesibilidad.
  • Integración y personalización. MathType se integra con LMS, CMS, editores HTML/XML y admite formatos personalizables, lo que lo hace ideal para proyectos escalables y necesidades diversas.
  • Compatibilidad con LaTeX y MathML. Asegura la compatibilidad con los lenguajes de marcado matemático estándar utilizados en entornos académicos, técnicos y editoriales.
  • Incluye ChemType para notación química. Edita y formatea ecuaciones químicas con una barra de herramientas dedicada para química inorgánica, lo que apoya a los profesionales científicos con necesidades específicas de formato.
editor chemtype
Ejemplo de fórmula química escrita con MathType de Wiris.

Invierte en una creación de contenido matemático más inteligente

En un mundo donde la precisión, la claridad y la accesibilidad son esenciales, las organizaciones ya no pueden tratar la escritura matemática como un aspecto secundario. Tanto si educas a futuros científicos, validas diseños de ingeniería o presentas modelos financieros complejos, la calidad de tu contenido matemático impacta directamente en cómo se entiende, se confía en él y se actúa en consecuencia.

Adoptar un editor matemático de nivel profesional no es solo una cuestión de conveniencia: es una decisión estratégica que respalda la coherencia, la colaboración y la eficiencia en toda la organización.

 

Ponte al día con la escritura matemática eficiente con MathType

Categorías
Sin categorizar

Creación de contenidos matemáticos: cómo Cambridge HOTmaths mejoró la publicación de matemáticas

Potenciar la enseñanza de las matemáticas con las herramientas adecuadas

Crear contenidos ricos en matemáticas para formatos digitales e impresos no es tarea fácil, especialmente cuando tu público incluye a miles de educadores y estudiantes de Australia y Nueva Zelanda. Para Cambridge HOTmaths, producir contenidos matemáticos visualmente precisos y accesibles era un gran reto. Eso cambió con MathType, un potente editor de ecuaciones de Wiris que permite a los usuarios crear y editar notaciones matemáticas en plataformas digitales e impresas. Se integra a la perfección con herramientas como Microsoft Word y es compatible con LaTeX, lo que lo hace ideal para educadores y creadores de contenido.

En esta historia de éxito, descubrirá cómo MathType revolucionó la creación de contenido en Cambridge HOTmaths, proporcionando a sus editores un control y una eficiencia totales, al tiempo que mejoraba la accesibilidad y la calidad del resultado.

Afrontar el reto de la publicación matemática digital

Antes de utilizar MathType, el proceso en Cambridge HOTmaths consistía en:

  • Insertar imágenes individuales para cada fracción o expresión matemática.
  • Depender de diseñadores gráficos para cualquier edición.
  • Gestionar problemas de formato y accesibilidad inconsistentes.

«Anteriormente utilizábamos imágenes para los cálculos y las fracciones, que tenían que enviarse al diseñador gráfico para cualquier modificación o corrección», explica Penny Redfearn, directora de contenidos de Cambridge HOTmaths.

Transición hacia una mejor creación de contenidos matemáticos

La adopción de MathType marcó un punto de inflexión. Con MathType, el equipo de contenidos obtuvo un control total sobre la edición de ecuaciones directamente en Microsoft Word. Los editores ya no tenían que insertar y alinear manualmente cada imagen de fracción: podían escribir todo como si fuera texto normal. «Los editores ya no necesitan insertar cada fracción individualmente como imagen y centrarla. Tenemos un control total sobre la creación de contenidos matemáticos que implican cálculos», afirma Penny.

Además, la transición a la salida basada en LaTeX con MathType mejoró significativamente la accesibilidad web. «Sustituir las imágenes por LaTeX mejoró significativamente la accesibilidad de nuestro sitio web».

hotmath mathtype

Cómo encaja MathType en su flujo de trabajo

Cambridge HOTmaths utiliza MathType principalmente de dos maneras:

  • Hojas de trabajo de Microsoft Word: MathType se utiliza para insertar todas las expresiones matemáticas directamente en los documentos, que luego se exportan a PDF para su distribución.
  • Ecuaciones del sitio web: MathType ayuda a generar LaTeX que se puede ajustar e integrar en el editor matemático LaTeX personalizado de su plataforma.

Aunque algunos ajustes finales de LaTeX todavía se realizan manualmente, MathType proporciona un punto de partida eficiente. «A menudo utilizamos MathType para obtener una plantilla LaTeX y luego la adaptamos», afirma Penny. MathType se ha convertido en un editor matemático LaTeX esencial para el equipo, ya que agiliza la creación de ecuaciones tanto impresas como basadas en la web.

Las herramientas matemáticas educativas adecuadas para las funciones adecuadas

Solo un pequeño equipo de Cambridge HOTmaths se encarga de la creación de contenidos, por lo que la facilidad de uso y la fiabilidad son fundamentales. La coherencia, la configuración de estilos y la compatibilidad con atajos de MathType han resultado ser muy valiosas. «Hemos configurado estilos para que todo sea coherente cada vez que creamos una nueva ecuación en el documento». Entre las numerosas herramientas matemáticas educativas disponibles, MathType destacó por su equilibrio entre funcionalidad, coherencia y facilidad de uso.

El equipo utiliza teclas de acceso rápido (por ejemplo, Ctrl+H para superíndice, Ctrl+L para subíndice), lo que hace que escribir ecuaciones sea rápido e intuitivo. «Llevo utilizando MathType desde que se creó… es fantástico».

Redefiniendo la creación de contenidos matemáticos en la educación

Para Cambridge HOTmaths, MathType es más que un editor matemático. Es un potenciador de la productividad, un mejorador de la accesibilidad y un facilitador de la creatividad. Su integración en su flujo de trabajo editorial ha ayudado a agilizar la creación de contenidos, reducir la dependencia de los diseñadores gráficos y garantizar una presentación matemática coherente en los formatos impresos y web.

Con la mirada puesta en ampliar la interactividad y la participación de los usuarios, MathType y el ecosistema Wiris en general están bien posicionados para apoyar a Cambridge HOTmaths en su continuo liderazgo en la innovación de la enseñanza de las matemáticas.

¿Quiere descubrir cómo MathType o WirisQuizzes pueden ayudar a su institución en la creación de contenidos matemáticos y en las necesidades de evaluación?

Descubre MathType

Categorías
Sin categorizar

Aprendizaje híbrido en la enseñanza de las matemáticas: por qué es importante combinar la enseñanza presencial y online

hybrid learning

El aprendizaje híbrido, también conocido como aprendizaje combinado, es un enfoque educativo que combina la enseñanza presencial tradicional con componentes digitales en línea. En lugar de tratar el aprendizaje en línea y el aprendizaje presencial como modos separados, el aprendizaje híbrido integra ambos de forma coordinada e intencionada. El objetivo no es simplemente alternar entre actividades presenciales y a distancia, sino diseñar una experiencia cohesionada que aproveche las ventajas de cada entorno: flexibilidad, accesibilidad, interacción y conexión personal. Este modelo ha ganado un gran impulso en los últimos años, especialmente en la enseñanza de las matemáticas, donde los conceptos abstractos y las diversas necesidades de aprendizaje se benefician de los distintos modos de participación.

El aprendizaje híbrido está transformando la forma en que enseñamos y aprendemos matemáticas. Al combinar las herramientas digitales con la enseñanza presencial, los educadores pueden ofrecer experiencias de aprendizaje más personalizadas, eficaces y atractivas.

Este enfoque no sustituye a los métodos tradicionales, sino que los mejora. Respeta los aspectos emocionales y cognitivos del aprendizaje y responde a la realidad de las aulas modernas, donde los alumnos tienen ritmos, estilos y circunstancias de aprendizaje diversos.

El aprendizaje combinado no es una moda, sino un cambio pedagógico que une la accesibilidad, la adaptabilidad y la conexión humana.

El poder de combinar la enseñanza de las matemáticas en línea y fuera de línea

El aprendizaje combinado en la enseñanza de las matemáticas crea una sinergia que ninguna de las dos modalidades puede lograr por sí sola. A medida que los educadores de matemáticas se adaptan a las necesidades cambiantes de los estudiantes y a las posibilidades tecnológicas, este modelo combinado ofrece:

  • Flexibilidad: los estudiantes pueden acceder a los recursos digitales en cualquier momento, lo que resulta especialmente útil para repasar o reforzar los conocimientos fuera del aula.
  • Interactividad: las herramientas en línea dan vida a los conceptos matemáticos a través de animaciones, simulaciones y plataformas interactivas de resolución de problemas.
  • Conexión humana: la enseñanza presencial fomenta el debate en tiempo real, el apoyo emocional y la retroalimentación inmediata.
  • Escalabilidad: los educadores pueden gestionar grupos grandes o diversos de manera más eficiente, ofreciendo apoyo personalizado cuando es necesario.

En matemáticas, donde los conceptos abstractos a menudo requieren una exploración iterativa, el aprendizaje híbrido potencia tanto la enseñanza guiada como el pensamiento independiente. Permite la repetición, la variación y el intercambio colaborativo, todos ellos elementos cruciales para una comprensión profunda. Al combinar la inmediatez del aprendizaje presencial con la accesibilidad de la enseñanza de las matemáticas en línea, los educadores pueden transformar verdaderamente su práctica.

Equilibrio entre estructura y autonomía en el aprendizaje híbrido

Una de las principales fortalezas del aprendizaje híbrido es su capacidad para equilibrar el marco de aprendizaje y la autonomía. El aprendizaje de las matemáticas exige ambas cosas: vías estructuradas para introducir y desarrollar habilidades de forma progresiva y autonomía para fomentar la exploración individual, la confianza y el pensamiento crítico. Las estrategias de aprendizaje combinado proporcionan el marco para este equilibrio, apoyando tanto la coherencia como la creatividad en las aulas de matemáticas.

En línea: proporcionar estructura y ritmo individual

Los entornos en línea ofrecen un marco estructurado para el aprendizaje. A través de módulos seleccionados, explicaciones paso a paso y comentarios automatizados, los estudiantes ganan en claridad y coherencia. La naturaleza autodidacta de las plataformas en línea permite a los estudiantes revisar conceptos, practicar a su propio ritmo y recibir orientación inmediata, lo que es especialmente valioso para dominar las habilidades fundamentales.

Herramientas como WirisQuizzes, una plataforma diseñada específicamente para evaluaciones de matemáticas y STEM, mejoran esta experiencia al ofrecer preguntas dinámicas y autocorregidas con variables aleatorias. Esto no solo proporciona oportunidades de práctica individualizadas, sino que también garantiza que los estudiantes se involucren activamente con el material en lugar de memorizar pasivamente las respuestas. La enseñanza de las matemáticas en línea empodera a los alumnos al ofrecerles control sobre su ritmo y áreas de enfoque, reforzando la competencia y la motivación.

Presencial: fomento del diálogo y el razonamiento profundo

La enseñanza fuera de línea, basada en el aula, añade los aspectos relacionales y espontáneos del aprendizaje. Las sesiones presenciales animan a los alumnos a articular su razonamiento, hacer preguntas y colaborar en problemas complejos. Los profesores pueden detectar malentendidos en tiempo real y adaptar las explicaciones. Estas interacciones desarrollan las habilidades de comunicación matemática y ayudan a los alumnos a conectar la teoría con la práctica. Este componente en vivo del aprendizaje híbrido garantiza que las matemáticas sigan siendo una disciplina social, receptiva y centrada en el ser humano.

Juntas, estas modalidades se refuerzan mutuamente. La estructura sin autonomía puede parecer rígida; la autonomía sin estructura puede carecer de dirección. El aprendizaje híbrido alinea ambas.

Pensamiento visual y simbólico

Las matemáticas son tanto visuales como simbólicas. El aprendizaje híbrido apoya esta dualidad utilizando herramientas digitales para representar ideas abstractas y entornos de aula para interpretarlas y discutirlas.

Las plataformas en línea como WirisQuizzes o Learning Lemur (nuestra intuitiva plataforma matemática integrada con Google Classroom que ofrece cuestionarios personalizables, calificación automática y comentarios personalizados) pueden visualizar funciones, transformaciones geométricas o manipulaciones algebraicas de forma interactiva. Estas representaciones complementan el trabajo simbólico tradicional y ayudan a los alumnos a formar modelos mentales. Los entornos presenciales proporcionan entonces el espacio para reflexionar e interpretar estas representaciones con compañeros y educadores, consolidando así la comprensión.

school learning

Al pasar con fluidez de las visualizaciones en línea a la manipulación simbólica fuera de línea (y viceversa), los estudiantes refuerzan su comprensión conceptual. Este tipo de interacción dinámica es una ventaja clave del aprendizaje híbrido, ya que permite a los alumnos conectar diferentes formas de representación matemática de manera más eficaz.

Aplicaciones del aprendizaje híbrido en matemáticas en el mundo real

El aprendizaje híbrido no es solo un marco teórico, sino que se está poniendo en práctica en una amplia variedad de entornos educativos. Desde escuelas urbanas hasta centros de aprendizaje rurales, los educadores están diseñando formas innovadoras de integrar la enseñanza digital y presencial en sus clases de matemáticas. Estas aplicaciones prácticas demuestran cómo las estrategias de aprendizaje combinado pueden satisfacer diversas necesidades educativas sin perder calidad ni compromiso.

Entre las muchas instituciones que ya aplican el sistema de aprendizaje híbrido, podemos encontrar la 21K School (Reino Unido), la Universidad de Harvard (EE. UU.), el Instituto Tecnológico de Massachusetts (EE. UU.) y las escuelas públicas de Singapur.

Casos de uso en aulas de todo el mundo

  • Un profesor de secundaria da la vuelta al aula: los alumnos ven vídeos instructivos y completan ejercicios guiados en casa, mientras que el tiempo de clase se utiliza para la resolución colaborativa de problemas.
  • Un profesor universitario alterna evaluaciones digitales y talleres presenciales, combinando la escalabilidad online con el apoyo práctico en directo.
  • Un centro comunitario en una zona con poca conectividad utiliza materiales interactivos descargados durante la semana y organiza clubes de matemáticas los fines de semana con educadores voluntarios.

Estos modelos del mundo real muestran cómo el aprendizaje híbrido puede adaptarse a diferentes contextos, buscando siempre optimizar tanto el acceso como el compromiso.

Una visión de la tecnología centrada en el ser humano: el enfoque de Wiris

Wiris se esfuerza por mantener una perspectiva moderna y tecnológica sin perder de vista la esencia humana y natural de la educación y la investigación científica. En Wiris creemos que la verdadera innovación no se consigue a expensas de la conexión personal, sino que se construye sobre ella. Esta filosofía encaja perfectamente con el modelo de aprendizaje híbrido, que combina las ventajas de las herramientas digitales con el valor insustituible de la enseñanza presencial.

Wiris diseña herramientas que reflejan esta visión. Estas herramientas no pretenden sustituir a los educadores ni estandarizar el aprendizaje. Su objetivo es empoderar a profesores y alumnos dentro del modelo híbrido que abraza este equilibrio entre estructura y autonomía, razonamiento visual y simbólico, alcance digital y conexión humana.

WirisQuizzes, por ejemplo, apoya la educación híbrida con cuestionarios de matemáticas personalizables y calificados automáticamente, basados en variables aleatorias, lo que garantiza un aprendizaje individualizado al tiempo que se mantiene el rigor académico.

MathType complementa este enfoque proporcionando un editor intuitivo para escribir notación matemática en múltiples plataformas, lo que permite una comunicación simbólica fluida tanto en entornos de aprendizaje digitales como en físicos.

LearningLemur, nuestra intuitiva plataforma matemática diseñada específicamente para Google Classroom, ofrece cuestionarios interactivos y personalizables con calificación automática y comentarios personalizados. Transforma la forma en que los estudiantes se involucran con los ejercicios matemáticos, proporcionando apoyo visual y contenido adaptable que se ajusta a cualquier estrategia de aprendizaje híbrida.

Aceptando el futuro de la enseñanza de las matemáticas

A medida que la línea entre las aulas digitales y físicas sigue difuminándose, aceptar el aprendizaje híbrido no es solo una opción: es una necesidad. Con la metodología y las herramientas adecuadas, podemos construir un futuro de la enseñanza de las matemáticas que sea inclusivo, adaptable y profundamente conectado con las necesidades tanto de los estudiantes como de los educadores.

Descubre cómo Wiris apoya el aprendizaje híbrido aquí.

Descubre cómo Wiris apoya el aprendizaje híbrido aquí

Categorías
Sin categorizar

Copiar en clase: evítalo con cuestionarios matemáticos de preguntas aleatorios

exam university

El aprendizaje online tiene un problema de trampas, y está creciendo

A medida que la educación cambia rápidamente a formatos online e híbridos, la deshonestidad académica se está volviendo más frecuente y difícil de detectar. Una revisión exhaustiva en la revista científica Springer Nature Link sobre el comportamiento de los estudiantes reveló que las trampas en los exámenes en línea aumentaron del 29,9 % antes de la COVID al 54,7 % durante la pandemia. 

Un estudio publicado en la revista Online Learning Journal examinó los exámenes online sin supervisión en un curso introductorio de biología con un gran número de alumnos. Utilizando los registros de actividad del LMS para detectar si los estudiantes se alejaban de la ventana del examen, los investigadores descubrieron que hasta el 70 % de los estudiantes lo hacían, a menudo en la mayoría de las preguntas. Las apelaciones a la integridad de los estudiantes o las promesas de honor tuvieron poco efecto, pero una simple advertencia sobre la posible detección, combinada con una política de sanciones, redujo este comportamiento a solo el 15 %. Este estudio demuestra claramente que la forma en que se diseña un examen —y la percepción que tienen los estudiantes de la supervisión— tiene un impacto mucho mayor en la honestidad académica que la propia tecnología utilizada.

Estas cifras ponen de relieve una tendencia preocupante: a medida que aumenta la dependencia del uso compartido de pantallas, las aplicaciones de mensajería y la IA generativa, las medidas tradicionales contra las trampas tienen dificultades para seguir el ritmo. Aunque la mayoría de las instituciones promueven la honestidad académica, los entornos digitales introducen nuevas vulnerabilidades que los exámenes tradicionales no tienen en cuenta. Ahí es donde la tecnología puede ayudar a los educadores a cambiar el rumbo.

Los riesgos de la falta de honestidad académica en las evaluaciones online

El aprendizaje digital ofrece flexibilidad, pero también pone de manifiesto las deficiencias en el control y la integridad de las evaluaciones. En particular, las pruebas de matemáticas y las evaluaciones de STEM se encuentran entre las más afectadas. ¿Por qué?

  • Los estudiantes pueden copiar las soluciones de sus compañeros en tiempo real. Durante los exámenes o pruebas online, los estudiantes pueden comunicarse fácilmente a través de aplicaciones de mensajería, videollamadas o pantallas compartidas. En muchos casos, esto les permite colaborar durante evaluaciones que están pensadas para ser individuales. La falta de supervisión presencial hace que la copia en tiempo real sea mucho más difícil de detectar que en un aula física.
  • Las plataformas para compartir respuestas suelen publicar colecciones completas de preguntas y respuestas de exámenes tomadas de cursos reales. Esto permite a los estudiantes buscar problemas específicos y encontrar soluciones exactas, lo que facilita hacer trampa, especialmente en las evaluaciones online. Estas plataformas suponen una grave amenaza para la integridad académica.
  • La verificación de la identidad es difícil en entornos no supervisados. Sin procedimientos de inicio de sesión seguros o herramientas de supervisión, resulta difícil garantizar que el estudiante que realiza un examen online sea realmente el que está matriculado en el curso. Esto abre la puerta a la suplantación de identidad, a los servicios de realización de exámenes a sueldo y a otras formas de fraude académico que son difíciles de rastrear a posteriori.
  • Los bucles de retroalimentación automática permiten repetir los intentos hasta acertar. Muchos sistemas de cuestionarios online ofrecen retroalimentación inmediata e intentos ilimitados sin ninguna variación en las preguntas. Aunque esto es útil para el aprendizaje formativo, puede ser objeto de abuso durante las evaluaciones sumativas, ya que los estudiantes pueden adivinar repetidamente o probar respuestas hasta encontrar la correcta, en lugar de comprender los conceptos subyacentes.

cheating math text

Cuestionarios matemáticos aleatorios: una estrategia inteligente para la honestidad académica

Para proteger la integridad de las evaluaciones matemáticas onlline, muchas instituciones están recurriendo a pruebas matemáticas aleatorias. Estas evaluaciones utilizan contenido basado en variables para generar versiones únicas del mismo problema para cada alumno.

Por qué funciona la aleatoriedad

La aleatoriedad es eficaz porque garantiza que cada estudiante reciba una versión única del mismo problema. Al generar diferentes conjuntos de variables, resulta casi imposible que los alumnos compartan respuestas o copien unos de otros. Este enfoque mantiene la misma estructura lógica y los mismos objetivos de aprendizaje para todos, pero con entradas variables que requieren una resolución independiente. También permite a los educadores regenerar automáticamente los problemas, escalando las evaluaciones sin comprometer la integridad. En última instancia, los cuestionarios matemáticos aleatorios reflejan los entornos de resolución de problemas del mundo real, en los que las condiciones cambian y la memorización por sí sola es insuficiente, lo que anima a los estudiantes a aplicar conceptos en lugar de recordar patrones. Los cuestionarios aleatorios no solo disuaden de la falta de honestidad académica, sino que también promueven un aprendizaje más profundo al fomentar estrategias individuales de resolución de problemas.

Insert random variables into a math question using WirisQuizzes. Inserta variables aleatorias en una pregunta matemática utilizando WirisQuizzes.

 

Cómo WirisQuizzes previene la falta de honestidad académica

WirisQuizzes es la sólida solución de evaluación de Wiris diseñada específicamente para la educación STEM. Permite a los educadores crear preguntas matemáticas ricas y dinámicas adaptadas al contexto de cada estudiante. Al introducir variables aleatorias, la plataforma genera versiones prácticamente ilimitadas del mismo problema, lo que desalienta las trampas y promueve una participación más profunda. Su motor de calificación inteligente automatiza la corrección y ofrece comentarios inmediatos, lo que fomenta el aprendizaje a través de la exploración y la repetición.

WirisQuizzes ofrece una función integrada de generación de variables aleatorias diseñada específicamente para contextos matemáticos y STEM. A diferencia de las plataformas de cuestionarios genéricas, WirisQuizzes comprende la estructura de las matemáticas y permite a los educadores definir plantillas de preguntas flexibles, pero pedagógicamente coherentes.

Con WirisQuizzes, los educadores pueden:

  • Definir rangos de variables para valores como x, a, b o θ.
  • Crear múltiples condiciones para garantizar resultados solucionables y significativos.
  • Aleatorizar parámetros numéricos y algebraicos.
  • Utilizar la lógica de validación automática para verificar las respuestas correctas por versión.
  • Previsualizar múltiples versiones de cuestionarios antes de implementarlas.

Este enfoque dinámico permite generar cientos de variaciones de cuestionarios a partir de un único modelo de pregunta, lo que mantiene las evaluaciones justas, seguras y escalables.

Aplicaciones en el mundo real: desde escuelas hasta universidades

La eficacia de los cuestionarios matemáticos aleatorios impulsados por WirisQuizzes se ha demostrado en varios niveles educativos:

Educación secundaria

En los institutos y colegios, los profesores utilizan WirisQuizzes para generar tareas y cuestionarios personalizados adaptados a cada alumno. Aunque los problemas evalúan los mismos conceptos, cada alumno recibe una versión única con variables diferentes. Esto reduce significativamente las oportunidades de copiar entre compañeros, al tiempo que se mantiene la alineación con el plan de estudios. Como resultado, los alumnos se involucran más profundamente con el material y se responsabilizan más de su proceso de aprendizaje.

Educación superior

En los institutos y universidades, los profesores confían en WirisQuizzes para realizar evaluaciones justas y seguras para grupos grandes sin tener que crear manualmente docenas o cientos de versiones diferentes de exámenes. Mediante el uso de variables aleatorias para generar problemas únicos pero equivalentes, los educadores pueden mantener la integridad académica incluso en exámenes parciales y finales de gran importancia. Esto es especialmente valioso en cursos STEM con un gran número de matriculados, como cálculo, álgebra lineal y estadística.

Plataformas de aprendizaje online

Las plataformas EdTech y los proveedores de aprendizaje online integran WirisQuizzes en sus sistemas de gestión del aprendizaje (LMS) para ofrecer evaluaciones seguras y escalables a una amplia base de usuarios. La generación aleatoria de preguntas garantiza que cada alumno se enfrente a un reto único, lo que dificulta mucho más compartir respuestas o copiar en masa. En combinación con la retroalimentación inmediata y la calificación inteligente, este enfoque favorece el aprendizaje adaptativo y altos niveles de integridad académica entre miles de usuarios.

Más que prevención: promover la honestidad académica por diseño

Prevenir la deshonestidad académica es solo una parte de la ecuación. Herramientas como WirisQuizzes también fomentan la honestidad académica al promover el pensamiento independiente y el aprendizaje personalizado.

Cuando los estudiantes saben que cada problema es único para ellos, son más propensos a involucrarse con el material en lugar de memorizar soluciones, desarrollar el pensamiento crítico y la comprensión conceptual y confiar en que sus esfuerzos se evalúan de manera justa. Este cambio de mentalidad contribuye a una cultura de integridad.

Acaba con las trampas mediante la aleatorización

En una era en la que se puede hacer trampa con unos pocos clics, la prevención debe ser proactiva, no punitiva. Los cuestionarios matemáticos aleatorios proporcionan una forma inteligente y escalable de garantizar evaluaciones justas y promover la honestidad académica.

WirisQuizzes permite a los educadores crear evaluaciones matemáticas dinámicas y basadas en variables que son seguras y se centran en el estudiante.

Prevén la falta de honestidad académica con WirisQuizzes

Prevén las tampas en el aula con WirisQuizzes

Categorías
Sin categorizar

Impulsando la innovación en las herramientas de evaluación matemática: cómo ASSISTments utiliza MathType

assessment mathtype

Transformando el contenido matemático digital en las aulas reales

En el vertiginoso mundo del contenido matemático digital, la precisión y la claridad son fundamentales para un aprendizaje eficaz. ASSISTments, una plataforma matemática en línea gratuita para los grados de K12, permite a los profesores asignar problemas matemáticos y proporcionar a los alumnos comentarios instantáneos. Con miles de alumnos y educadores que confían en la plataforma cada día, ASSISTments necesitaba una solución escalable, precisa y accesible para manejar notaciones matemáticas complejas. Aquí entra en juego MathType, la herramienta que potencia las expresiones matemáticas tanto en la creación de contenidos como en las respuestas de los alumnos dentro de sus herramientas de evaluación matemática.

Cuando las ecuaciones eran confusas: los retos antes de MathType

Como plataforma de evaluación, ASSISTments se enfrentaba a una demanda creciente de coherencia en la creación de contenidos matemáticos y claridad en la expresión. Según Ryan Emberling, director de ingeniería de la Fundación ASSISTments, uno de sus mayores puntos débiles era el formato:

«Era un problema para los alumnos escribir cosas como sqrt() para expresar sus respuestas y para los profesores entender esas respuestas».

Generar e interpretar notaciones matemáticas sin un editor estandarizado provocaba confusión e ineficiencia.

Además, crear expresiones matemáticas a gran escala era complejo. «Incluso incrustar estas ecuaciones como imágenes era un reto», afirma Ryan. El equipo necesitaba una herramienta que agilizara tanto la creación como la lectura de contenidos matemáticos, una herramienta que facilitara las evaluaciones matemáticas en línea tanto para los profesores como para los estudiantes.

La solución MathType: una solución perfecta para ASSISTments

ASSISTments implementó MathType en toda su plataforma, incorporándolo tanto en la creación de preguntas como en los campos de respuesta de los estudiantes. Esto permitió escribir, mostrar e interpretar las matemáticas de forma coherente a lo largo de todo el proceso de aprendizaje. Como explica Ryan, «utilizamos MathType tanto en las preguntas como en las respuestas de los estudiantes».

El impacto fue inmediato. Los profesores obtuvieron una interfaz fiable y familiar para crear problemas con una notación matemática clara. Los alumnos podían escribir expresiones de forma intuitiva sin necesidad de memorizar la sintaxis. Y lo más importante, la plataforma logró la estandarización en toda su amplia biblioteca de problemas matemáticos.

Hacer funcionar las matemáticas a gran escala: la implementación en acción

Para mejorar la calidad de la enseñanza de las matemáticas no basta con tener buenas intenciones: se necesitan las herramientas adecuadas, implementadas de forma cuidadosa. ASSISTments sabía que para lograr un contenido matemático coherente y accesible para miles de usuarios era necesario cuidar los detalles desde el principio.

Flujo de trabajo principal: cómo utilizan la plataforma los profesores y los alumnos

ASSISTments comenzó identificando su principal reto: crear una interfaz fácil de usar para las matemáticas que ayudara a los autores de contenidos y mejorara la claridad para los alumnos. Como explica Ryan, esta necesidad surgió de la funcionalidad principal de la plataforma:

«Los profesores asignan tareas a sus alumnos […] y estos completan las tareas asignadas y obtienen puntuaciones automáticamente».

Una solución flexible para diversas necesidades

Usando MathType, la plataforma se adaptó para dar servicio a múltiples tipos de usuarios. Tanto si creaban preguntas de álgebra como si enviaban respuestas abiertas, los usuarios interactuaban con la misma herramienta de entrada matemática coherente. Esta uniformidad se ajustaba perfectamente a las necesidades del plan de estudios.

Integración sin complicaciones

Gracias a la flexible integración de MathType, la implementación fue sencilla. Su perfecta integración permitió al equipo de ingeniería centrarse en crear mejores contenidos en lugar de gestionar las complejidades del formato.

results math assessment

Qué cambió: resultados que mejoraron la creación de contenidos matemáticos

Cuando ASSISTments integró MathType por primera vez, la decisión no se basó solo en mejorar su plataforma, sino en elegir un socio que pudiera crecer junto con su visión. A lo largo de los años, nunca han tenido que reconsiderar esa elección. MathType ha satisfecho constantemente sus necesidades cambiantes sin necesidad de realizar grandes modificaciones o cambios de integración.

Esta fiabilidad a largo plazo se ha convertido en la piedra angular de su estrategia de innovación. A medida que ASSISTments ampliaba las capacidades de su plataforma y escalaba sus ofertas, MathType apoyaba estos avances a la perfección. Desde evaluaciones en el aula hasta implementaciones de investigación a gran escala, la adaptabilidad de MathType ha demostrado ser indispensable.

Elegir MathType desde el principio significó contar con la herramienta adecuada desde el primer día, una herramienta que sigue satisfaciendo las complejas necesidades de creación de contenidos matemáticos, independientemente de cómo evolucione la plataforma.

 

Próximos pasos: ampliar la innovación y la accesibilidad

De cara al futuro, la accesibilidad sigue siendo una prioridad clave. «Desde el punto de vista de la accesibilidad, nos cuesta mucho el uso de imágenes. […] Sería preferible que se pudieran convertir en texto que el lector de pantalla pudiera leer más directamente», explica Ryan. El equipo está estudiando activamente cómo podría evolucionar MathType para mejorar la compatibilidad con los lectores de pantalla y ajustarse a las mejores prácticas de accesibilidad.

Más allá de la accesibilidad, ASSISTments está ampliando los límites de la automatización.

«Nos interesa ampliar los límites de los tipos de problemas que podemos calificar automáticamente: problemas gráficos, manipulativos… para garantizar que los estudiantes sigan recibiendo comentarios inmediatos y ahorrar a los profesores la necesidad de calificar», afirma Ryan.

Se espera que MathType desempeñe un papel clave en la ampliación de esta visión.

Conclusión: el impacto duradero de MathType en ASSISTments

La colaboración entre ASSISTments y MathType pone de manifiesto el papel fundamental que desempeñan las herramientas de evaluación matemática bien integradas en la educación moderna. Con MathType, ASSISTments ha transformado su enfoque de la creación de contenidos matemáticos, mejorando la comunicación, la accesibilidad y la escalabilidad.

Las ideas de Ryan Emberling muestran que la innovación en los contenidos matemáticos digitales no se limita a la tecnología: se trata de diseñar herramientas que empoderen a los usuarios en todos los niveles del proceso de aprendizaje.

¡Transforma tu plataforma con MathType!

Hacer el trabajo de la gente en STEM más significativo