Conjetura de Collatz

Las conjeturas matemáticas son enigmas que desafían la mente humana: problemas aparentemente sencillos que, a pesar de haberse verificado en millones de casos, aún carecen de una demostración. Son pregunta aparentemente intuitivas que esconden una complejidad inesperada.

Lo fascinante de las conjeturas es que, en muchos casos, se pueden verificar empíricamente, es decir, comprobarse mediante una cantidad enorme de ejemplos numéricos. Sin embargo, esta comprobación no satisface a los matemáticos, quienes buscan una demostración teórica, una prueba sólida que valide el enunciado en su totalidad. Sin dicha demostración, las conjeturas permanecen como retos abiertos.

La conjetura de Collatz es un ejemplo perfecto de este tipo de misterio matemático. Fue propuesta en 1937 por Lothar Collatz y su enunciado es el siguiente:

Escogiendo un número entero positivo cualquiera aplicaremos los siguientes pasos:

➔ Si el número es par, lo dividiremos entre 2.

➔ Si el número es impar, lo multiplicaremos por 3 y luego le sumaremos 1.

➔ Repetiremos el proceso con el nuevo número obtenido

La conjetura dice que, sin importar el número con el que empieces, siempre llegarás al número 1. Una vez que llegas al 1, el proceso se repite indefinidamente: 1 →4 →2 →1

Formalmente, esto se puede escribir como la función f=N →N definida como:

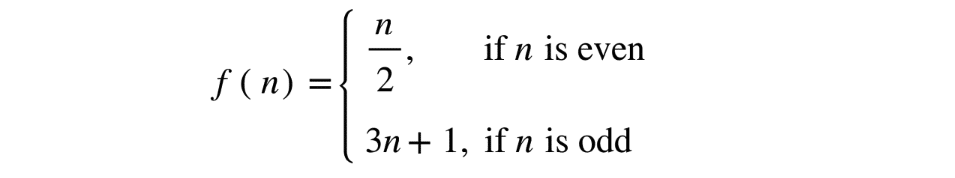
Dos ejemplos ilustrativos de la Conjetura de Collatz

Veamos un par de ejemplos sencillos.

Tomemos el número n=6 y apliquemos los pasos de la conjetura de Collatz:

1. 6 es par así que lo dividimos entre 2: 6/2=3
2. 3 es impar por lo que multiplicamos por 3 y le sumamos 1: 3·3+1=10
3. 10 es par así que lo dividimos entre 2: 10/2=5
4. 5 es impar por lo que multiplicamos por 3 y le sumamos 1: 3·5+1=16
5. 16 es par así que lo dividimos entre 2: 16/2=8
6. 8 es par así que lo dividimos entre 2: 8/2=4
7. 4 es par así que lo dividimos entre 2: 4/2=2
8. 2 es par así que lo dividimos entre 2: 2/2=1

Una vez que llegamos a 1, el proceso se repite: 1 →4 →2 →1.

Así que observamos que comenzando con n=6 la conjetura se satisface.

Tomemos ahora el número n=21 y apliquemos los pasos de la conjetura de Collatz:

1. 21 es impar por lo que multiplicamos por 3 y le sumamos 1: 21·3+1=64
2. 64 es par así que lo dividimos entre 2: 64/2=32
3. 32 es par así que lo dividimos entre 2: 32/2=16
4. 16 es par así que lo dividimos entre 2: 16/2=8
5. 8 es par así que lo dividimos entre 2: 8/2=4
6. 4 es par así que lo dividimos entre 2: 4/2=2
7. 2 es par así que lo dividimos entre 2: 2/2=1

De nuevo, llegamos al número 1.

Ambos ejemplos han llegado al número 1, pero en un número distinto de pasos. De hecho, aunque 21 es un número mayor, llegó a 1 en menos pasos que 6. Esta conjetura ha sido probada para una increíble cantidad de números, hasta más de 2ˆ60 = 1.152.921.504.606.846.976 casos, sin encontrar ningún contraejemplo. Sin embargo, aún sigue siendo un misterio si existe algún número que no cumpla la conjetura.

Representaciones gráficas de la conjetura de Collatz

El grafo dirigido de órbitas es una representación visual que facilita la comprensión del comportamiento de los números bajo las reglas de la conjetura de Collatz. En este gráfico, cada número se representa como un nodo, y las conexiones entre ellos muestran los pasos que sigue el proceso de la conjetura. Al seguir la secuencia de un número, los nodos se conectan mediante flechas que indican cómo se transforma el número en cada paso. Aunque en general se omiten los números pares en la representación para simplificar, el gráfico ilustra cómo los números «orbitan» alrededor de ciertos ciclos, como el 1 →4 →2 →1.

En la imagen anterior, podemos ver un ejemplo del grafo dirigido de órbitas, donde hemos resaltado en amarillo los números 3 y 21. El número 3 hace referencia a la secuencia del 6, ya que en este gráfico se omiten los números pares para simplificar la visualización.

Observamos que el 21 llega rápidamente a 1, ya que solo pasa por números pares en su camino, como vimos en el ejemplo anterior. Por otro lado, el número 6 primero se convierte en 3, luego pasa por el número 5, que finalmente lo llevará a 1 tras varios pasos con números pares.

También es interesante notar que el número 9, aunque relativamente pequeño, sigue una secuencia más larga: pasa por los números 7, 11, 17, 13 y 5, y finalmente llega a 1, tras un total de 19 pasos.

A continuación, se presenta un gráfico en el que el eje X muestra los distintos valores enteros iniciales, mientras que el eje Y representa el número de iteraciones necesarias para que cada número alcance el valor 1.

En resumen, la conjetura de Collatz es un problema aparentemente sencillo que, a día de hoy, aún no tiene una demostración formal. Aunque pueda parecer un enunciado de poca relevancia o utilidad práctica, esta conjetura tiene aplicaciones en diversos campos, como la teoría de números, la criptografía, el análisis de algoritmos y la inteligencia artificial. En estos campos, el estudio de secuencias complejas y su comportamiento bajo reglas específicas puede ofrecer valiosos insights para resolver problemas más mayores y entender patrones matemáticos.

¿Te ha fascinado la simplicidad y el misterio de la conjetura de Collatz? Ahora es tu turno: toma el número 27 y comienza la sucesión. ¿Cuántos pasos necesitarás para llegar al 1?

Si este desafío te atrapó, ¡no lo guardes solo para ti! Compártelo con otros curiosos de los enigmas matemáticos y descubrid juntos quién resuelve el reto más rápido.