Torres de Hanoi: Un desafío de matemáticas y programación

Las Torres de Hanoi son uno de los rompecabezas más emblemáticos en el ámbito de las matemáticas y la teoría de la computación. Con su estructura sencilla y reglas claras, este problema ha cautivado a matemáticos y aficionados por igual, convirtiéndose en un reto intrigante desde su creación.

Según la leyenda, las Torres de Hanoi fueron concebidas por un grupo de monjes en un antiguo templo de la India. En el centro de este templo, se erigían tres pilares de oro sobre los que descansaban 64 discos de diferentes tamaños, dispuestos en el primer pilar de manera ordenada: el disco más grande en la base, y sobre él, discos de tamaños progresivamente más pequeños, hasta llegar al disco más pequeño, colocado en la parte superior.

El objetivo de los monjes era mover todos los discos del primer pilar al tercero, usando el pilar central como auxiliar. Para cumplir esta tarea, debían seguir un conjunto de reglas estrictas:

1. Solo se puede mover un disco a la vez.
2. Un disco nunca puede colocarse sobre otro más pequeño.

Cuenta la leyenda, que cuando todos los discos fuesen trasladados correctamente al último pilar, el mundo llegaría a su fin. Sin embargo, ¿qué tan cerca está el fin del mundo, realmente?

¿Cuánto tiempo tomaría cumplir con este desafío? Este desafío fue introducido oficialmente por el matemático francés Édouard Lucas en 1883, como parte de sus investigaciones en teoría de números y rápidamente se convirtió en un problema popular.

A continuación, analizaremos la resolución de este problema desde una perspectiva matemática, desglosando sus principios clave, y exploraremos cómo se transforma en un interesante desafío de programación.

 

La recursión como solución al rompecabezas

El reto de las Torres de Hanoi no solo está en mover los discos de un pilar a otro, siguiendo las reglas estrictas, sino en cuántos movimientos son necesarios para resolver el problema de trasladar discos desde el pilar de origen al pilar de destino.

La forma más eficiente de abordar este problema es a través de la recursión, una técnica fundamental en programació. La recursión permite dividir el problema en subproblemas pequeños, donde la solución de cada subproblema lleva a la solución del problema original.

En el caso de las Torres de Hanoi, la recursión se aplica de manera natural y podemos dividir el problema de mover discos en tres etapas:

➔ Mover los primeros n-1 discos del pilar de origen al pilar auxiliar, usando el pilar de destino como auxiliar.
➔ Mover el disco más grande (el disco n) del pilar de origen al pilar de destino.
➔ Mover los discos n-1 del pilar auxiliar al pilar de destino, utilizando el pilar de origen como auxiliar.

Este patrón se repite recursivamente, reduciendo el número de discos en cada paso hasta llegar a un caso base, donde solo queda un disco que se mueve directamente.

En términos matemáticos, el número mínimo de movimientos para resolver el problema con n discos es el mismo que el número de movimientos para discos n-1, más uno para mover el disco más grande, más el número de movimientos para discos n-1 otra vez. Esta fórmula da como resultado:

TH( n ) = TH( n – 1 ) + 1 + TH( n – 1 ) = 2TH( n – 1 ) + 1

Donde TH( n ) representa el número de movimientos para n discos.

A partir de la fórmula anterior, iremos sustituyendo cada TH( i ) por su expresión correspondiente hasta llegar a TH( 1 ). Después sustituiremos TH( 1 ) por 1, ya que, con un solo disco, es posible moverlo directamente al pilar de destino, lo que justifica que el número mínimo de movimientos en este caso sea 1.

Veamos la expresión desarrollada:

• Sustituimos primero TH( n – 1 ), y obtenemos: 

TH( n ) = 2TH( n – 1 ) + 1 

TH( n ) = 2( 2TH( n – 2 ) + 1 ) + 1 = 2²TH( n – 2 ) + 3

• Ahora sustituimos TH( n – 2 ):

TH( n ) = 2²TH( n – 2 ) + 3

TH( n ) = 2²( 2TH( n – 3 ) + 1 ) + 3 = 2³TH( n – 3 ) + 7

• Si seguimos sustituyendo de esta forma, llegaremos a una fórmula general:

TH( n ) = 2^k  TH( n – k ) + (2^k – 1)

Donde k es el número de pasos que damos hacia atrás en la recursión.

• Para k = n – 1 llegaremos a TH( 1 ), el caso base:

TH( n ) = 2²TH( n – 2 ) + 3

Sabemos que TH( 1 ) = 1, entonces obtenemos:

TH( n ) = 2^{n – 1} · 1 + ( 2^{n – 1} – 1 ) = 2ⁿ – 1

Hemos demostrado que el número de movimientos necesarios para resolver las Torres de Hanoi con n discos es:

TH( n ) = 2ⁿ – 1

Solución mediante inducción matemática

Otra manera de abordar la solución al rompecabezas de las Torres de Hanoi es utilizando inducción matemática, una técnica utilizada para demostrar que una afirmación es cierta para todos los números naturales, basándose en dos pasos fundamentales: el caso base y el paso inductivo.

En este caso, el objetivo es demostrar que para mover discos del primer pilar al tercero, se requieren 2ⁿ – 1  movimientos. Vamos a desglosar este proceso con una demostración por inducción.

Caso base:

Supongamos que tenemos solo un disco . En este escenario, es evidente que solo se necesita un movimiento para trasladar el disco desde el pilar de origen al pilar de destino. Es decir, para n = 1, el número de movimientos necesarios es 2¹ – 1 = 1, lo cual es cierto.

Paso inductivo:

Ahora, supongamos que la afirmación es cierta para n = k, es decir, que para mover k discos se necesitan 2^k – 1 movimientos. Lo que debemos demostrar es que la afirmación también se cumple para n = k + 1.

Para mover k + 1 discos, primero necesitamos mover los discos superiores del pilar de origen al pilar auxiliar, utilizando el pilar de destino como auxiliar. Según nuestra hipótesis inductiva, esto tomará 2^k – 1 movimientos.

Luego, movemos el disco más grande (el disco  k + 1) del pilar de origen al pilar de destino, lo cual requiere 1 movimiento.

Finalmente, movemos los k discos del pilar auxiliar al pilar de destino, utilizando el pilar de origen como auxiliar, lo que también tomará 2^k – 1 movimientos, según nuestra hipótesis inductiva.

Por lo tanto, el total de movimientos necesarios para mover k + 1 discos es:

(2^k – 1) + 1 + (2^k – 1) = 2^k+1 – 1

De esta forma, hemos demostrado que si la afirmación es cierta para n = k, también lo es para n = k + 1.

Como hemos observado que es cierto para 1, mediante inducción matemática podemos concluir que para n discos, el número mínimo de movimientos necesarios es 2ⁿ – 1.

Volviendo a la leyenda, si los monjes fueran extremadamente rápidos y pudieran mover un disco en tan solo un segundo, tendríamos que calcular cuántos segundos tomarían para completar el desafío con 64 discos. Según la fórmula 2⁶⁴ – 1, el número total de movimientos sería aproximadamente 18,4 quintillones de movimientos. Si asumimos que cada movimiento toma 1 segundo, esto nos da 18,4 quintillones de segundos. Si convertimos estos segundos en años, obtenemos que el tiempo total sería de aproximadamente 581,4 mil millones de años. Así que, si seguimos la leyenda al pie de la letra, ¡el fin del mundo estaría a una distancia increíblemente lejana!

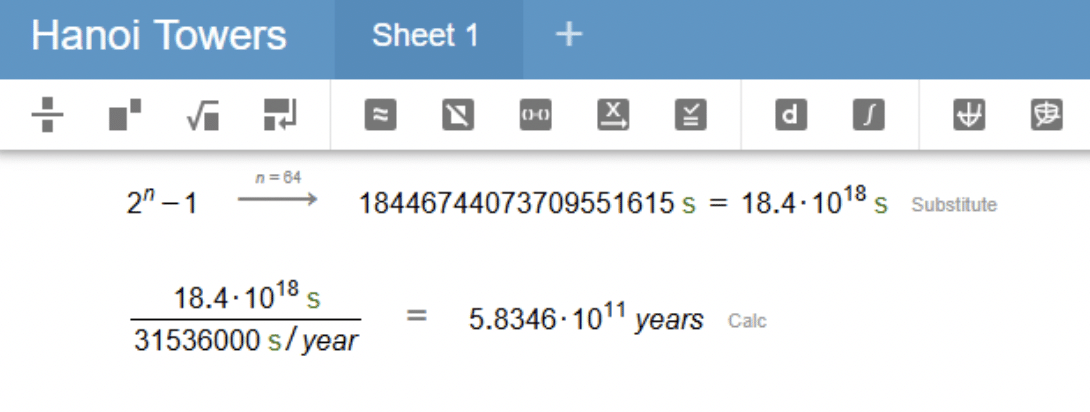
Observamos que la función que describe el número de movimientos necesarios para resolver las Torres de Hanoi es exponencial, lo que significa que crece rápidamente a medida que aumentamos el número de discos. En el siguiente gráfico, podemos ver visualmente cómo esta función se dispara, ilustrando claramente el crecimiento exponencial.

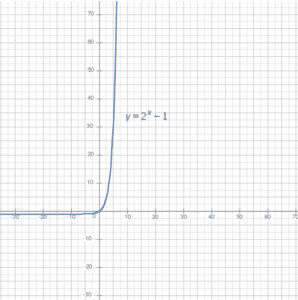
Este soporte visual nos permite confirmar, una vez más, que completar el desafío con 64 discos llevaría un tiempo verdaderamente impresionante.

Si te ha gustado este desafío matemático y te ha sorprendido su solución ¡no dudes en compartir este artículo! Y si te atreves, pon a prueba tus habilidades resolviendo el rompecabezas de las Torres de Hanoi. ¿Lograrás mover los discos en el número exacto de pasos ? ¡Cuéntanos tu experiencia!