El problema de Monty Hall explicado como nunca antes lo habías visto

¿Qué es el problema de Monty Hall?

Originario del programa de televisión «Let’s Make a Deal», el problema de Monty Hall presenta el siguiente escenario:

1. Te muestran tres puertas.
2. Detrás de una puerta hay un coche (tu objetivo), detrás de las otras dos hay cabras.
3. Tú eliges una puerta.
4. El presentador (Monty Hall), que sabe —y esto es muy importante— lo que hay detrás de cada puerta, abre una de las otras dos puertas, revelando una cabra.
5. A continuación, se te ofrece la oportunidad de cambiar tu elección por la puerta que queda sin abrir.

La pregunta es: ¿deberías cambiar? La intuición dice que no importa. Las matemáticas dicen lo contrario. 

A primera vista, mucha gente razona que, con dos puertas sin abrir, las probabilidades deben ser del 50 %: una puerta tiene un coche y la otra tiene una cabra, por lo que cambiar es como lanzar una moneda al aire. Otros se basan en su instinto de justicia y piensan que la intervención del presentador de alguna manera restablece las probabilidades. Algunos incluso argumentan que mantener su elección original «les da más seguridad» o que el presentador está tratando de engañarlos. Todos estos son atajos intuitivos comunes, e incorrectos, que ignoran cómo cambia la probabilidad cuando se introducen decisiones informadas. La explicación del problema de Monty Hall pone de manifiesto cómo nuestros instintos a menudo nos engañan en situaciones de incertidumbre.

Uno de los momentos más famosos relacionados con este rompecabezas fue cuando Marilyn vos Savant, conocida por tener el coeficiente intelectual más alto registrado, respondió a la pregunta de un lector al respecto en la revista Parade. Su consejo acertado de cambiar siempre provocó una gran controversia, y miles de lectores, entre ellos muchos doctores en matemáticas, insistieron en que estaba equivocada. Spoiler: no lo estaba.

El problema de Monty Hall explicado también aparece en la película 21, lo que contribuyó a popularizarlo entre el público general como una paradoja de probabilidad alucinante que pone de relieve cómo nuestros instintos pueden fallarnos en situaciones probabilísticas.

La analogía de las 52 cartas: un avance intuitivo

Para comprender mejor el problema de Monty Hall explicado, utilicemos una baraja de 52 cartas para aclarar las cosas:

1. Imagina lo siguiente: alguien pone sobre la mesa una baraja completa de 52 cartas boca abajo y te dice que la ganadora es el as de picas.
2. Ahora es tu turno. Eliges una carta al azar de entre las 52 cartas boca abajo, pero aún no la miras.
3. A continuación, el presentador, que sabe dónde está el as de picas, descubre todas las cartas excepto la tuya y otra más. 
4. En este momento, te preguntan: ¿quieres quedarte con tu elección original o cambiar a la otra carta restante?

Curiosamente, aunque la mayoría de la gente tiende a quedarse con su elección original en la versión clásica de tres puertas del problema de Monty Hall, creyendo que ahora las probabilidades son iguales, este comportamiento suele cambiar drásticamente cuando se replantea el escenario utilizando 52 cartas. Ante la abrumadora improbabilidad de haber elegido la carta correcta desde el principio, la mayoría de los participantes eligen instintivamente cambiar. El dramático contraste en la probabilidad percibida hace que la lógica detrás del cambio sea mucho más clara, incluso para aquellos que lucharon con el dilema original.

¿Por qué tiene sentido el cambio? Hagamos algunos cálculos:

1. Probabilidad de que tu primera elección sea el as de picas: 1/52 (1,92 %)
2. Probabilidad de que la carta que no elegiste sea el as de picas: 51/52 (98,08 %) 

El cambio se convierte claramente en la opción racional. Esto se debe a que tu elección inicial solo tenía una probabilidad entre 52 de ser correcta, mientras que la carta restante sin revelar tiene ahora la probabilidad acumulada de las otras 51 cartas, lo que la hace mucho más probable de ser la ganadora. La misma lógica se aplica a la configuración original de tres puertas, aunque con diferencias numéricas menores: cambiar sigue aumentando tus probabilidades de 1/3 a 2/3, lo que ilustra cómo la información actualizada cambia el panorama de probabilidades.

Descifrando el código: por qué cambiar en el problema de Monty Hall tiene sentido matemático 

Volvamos a la situación original y simplifiquemos la configuración para poder explicar el problema de Monty Hall:

• Probabilidad de que tu primera elección sea el coche: 1/3 (33,33 %)
• Probabilidad de que el coche esté detrás de una de las otras dos puertas: 2/3 (66,66 %)

Monty Hall abre una puerta que sabe que tiene una cabra, no al azar, sino deliberadamente, para darte más información sin revelar la puerta ganadora. Esta acción no cambia el hecho de que la probabilidad inicial de que tu primera elección sea correcta siga siendo de 1/3. Sin embargo, dado que Monty Hall nunca revelará el coche, la probabilidad de 2/3 de que el coche esté en una de las dos puertas no elegidas se traslada ahora por completo a la puerta sin abrir que él no ha elegido. Por eso cambiar aumenta tus probabilidades: la acción de Monty Hall reduce la incertidumbre sin alterar las probabilidades originales. 

Para comprender la ventaja real de cambiar, imagina que juegas al problema de Monty Hall 300 veces. Si siempre te quedas con tu elección inicial, esperarías ganar aproximadamente 100 veces, ya que hay una probabilidad entre tres de que hayas elegido inicialmente la puerta correcta. Por otro lado, si siempre cambias después de que Monty revele una cabra, ganarías aproximadamente 200 veces. Esta clara diferencia ilustra cómo el cambio aprovecha la mayor probabilidad de que el premio no estuviera detrás de tu primera elección.

Generalización matemática: el problema de las N puertas

Aunque la versión clásica del problema de Monty Hall utiliza tres puertas, la lógica subyacente puede extenderse a cualquier número de opciones. Al aumentar el número de puertas, la ventaja contraintuitiva de cambiar se hace aún más evidente. Exploremos cómo varían las probabilidades cuando generalizamos el problema a n puertas.

Sea n el número total de puertas (n ≥ 3).

• Si te quedas, tu probabilidad de ganar es 1/n.
• Si cambias, tu probabilidad es (n-1)/n.

Para compararlas directamente, considera la relación entre los dos resultados: [(n-1)/n] dividido por [1/n] se simplifica a (n-1). Esto significa que cambiar te hace (n-1) veces más propenso a ganar que quedarte. Por ejemplo:

• Con 3 puertas, tienes 2 veces más probabilidades de ganar si cambias.
• Con 4 puertas, tienes 3 veces más probabilidades.
• Con 10 puertas, tienes 9 veces más probabilidades.

El número de puertas debe ser al menos tres, porque con dos puertas no hay espacio para que Monty revele una cabra sin ambigüedad, y con una puerta no hay elección que hacer. Por lo tanto, el problema solo tiene sentido lógico con n ≥ 3.

Esta variación ofrece otra forma de ver el problema de Monty Hall explicado en acción.

Aplicaciones del mundo real de la lógica de Monty Hall

Ahora que hemos explicado el problema de Monty Hall, puedes ver que es más que un simple rompecabezas peculiar. Tiene implicaciones reales en:

• Teoría de juegos: El problema de Monty Hall ilustra cómo pueden surgir estrategias óptimas en juegos probabilísticos en los que la información se revela gradualmente. Destaca el valor de actualizar las decisiones a medida que se dispone de nueva información, un principio esencial en el pensamiento estratégico.
• Toma de decisiones en condiciones de incertidumbre: en muchas situaciones de la vida real, como las inversiones financieras o las estrategias legales, nos enfrentamos a decisiones con información incompleta. La lógica de Monty Hall nos enseña que reevaluar las decisiones cuando surgen nuevos datos puede cambiar drásticamente los resultados, incluso cuando nuestro instinto nos sugiere lo contrario.
• Diagnósticos médicos: los médicos suelen comenzar con un conjunto de posibles diagnósticos y refinan sus evaluaciones basándose en los resultados de las pruebas. Al igual que Monty al revelar una cabra, los resultados negativos de las pruebas ayudan a eliminar opciones, desplazando las probabilidades hacia el diagnóstico correcto y enfatizando el beneficio de revisar las hipótesis iniciales.
• IA y aprendizaje automático: los algoritmos actualizan con frecuencia sus predicciones basándose en la retroalimentación y los nuevos datos, de forma muy similar a como el cambio mejora las posibilidades en el problema de Monty Hall. El problema subraya el valor de los modelos adaptativos que refinan los resultados a medida que se revela más información.

Visualiza el problema de Monty Hall explicado con CalcMe 

¿Quieres explorarlo visualmente? Utiliza CalcMe, una plataforma matemática dinámica de Wiris, para simular diferentes valores de n y ver cómo cambian las probabilidades.

CalcMe permite a los educadores y estudiantes crear exploraciones matemáticas interactivas utilizando variables, gráficos y scripts basados en la lógica. Es perfecto para recrear y explicar el problema de Monty Hall y comprenderlo.

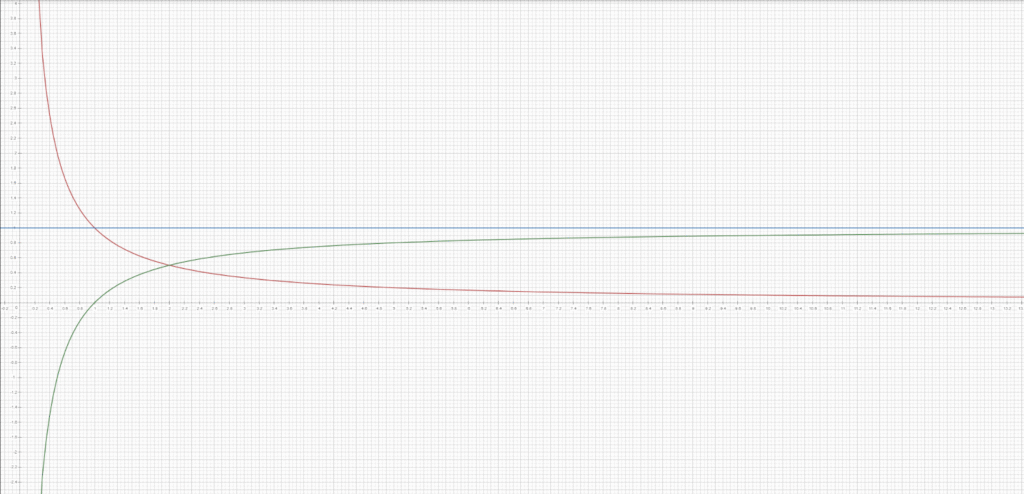
Fig. 1: La función verde representa la probabilidad de ganar el coche si cambias, la roja representa tus posibilidades si no cambias y la azul representa el 100 %.