Modo algoritmo para valores aleatorios: una función inteligente de LearningLemur

A la hora de diseñar experiencias de aprendizaje digital, los profesores de matemáticas se enfrentan a menudo a un reto habitual: cómo generar variedad en los ejercicios prácticos y, al mismo tiempo, mantener la relevancia y la solucionabilidad de los problemas, así como su alineación con los objetivos del plan de estudios. Ahí es donde entra en juego la automatización inteligente. LearningLemur, la plataforma desarrollada por Wiris, sigue evolucionando y ofrece a los profesores herramientas que combinan flexibilidad y precisión.

Por qué lo aleatorio no siempre es fiable en las evaluaciones matemáticas

Imagina que eres un profesor que crea ejercicios aleatorios sobre fracciones. Quieres que tus alumnos practiquen la suma de fracciones como 1/4 + 5/4. Sin embargo, si los valores varían aleatoriamente, la complejidad del problema cambia drásticamente. Una fracción como 4/2 se simplifica a un número entero, lo que la hace inútil para tu lección centrada en las fracciones. Un caso como 2/4 no está en su forma más simple, lo que puede confundir a los alumnos o introducir un objetivo de aprendizaje no deseado.

Otro problema común aparece en álgebra. Supongamos que quieres que los alumnos resuelvan una ecuación cuadrática. Para que la ecuación tenga soluciones reales, el discriminante (b² – 4ac) debe ser positivo. Si generas los coeficientes a, b y c aleatoriamente sin restricciones, puedes crear accidentalmente ecuaciones que solo tienen soluciones complejas, lo que va mucho más allá del alcance previsto de tu lección.

También puede encontrarse con problemas inesperados en temas más avanzados. En álgebra lineal, las matrices generadas aleatoriamente pueden no ser invertibles, lo que frustra el propósito de la actividad. O puede que necesite que los vectores sean paralelos, pero los valores aleatorios no controlados dan lugar a orientaciones completamente arbitrarias.

Estos ejemplos revelan el problema fundamental: los valores aleatorios por sí solos no son suficientes. Necesitamos una aleatoriedad inteligente, guiada por una lógica avanzada.

Por qué los profesores astutos eligen el Modo Algoritmo

La aleatoriedad puede ser increíblemente útil a la hora de crear ejercicios y evaluaciones matemáticas, pero a menudo trae más problemas que soluciones. Imagina asignar una hoja de ejercicios en la que cada alumno recibe una versión ligeramente diferente del mismo problema. Suena ideal, ¿verdad? Pero si esos valores aleatorios no se controlan, podrías terminar con ecuaciones sin solución, fracciones simplificadas que eluden tu objetivo o problemas de álgebra sin soluciones válidas.

Los profesores necesitan flexibilidad sin caos. Quieren que sus alumnos practiquen problemas diversos, pero solo dentro de los parámetros adecuados. Ahí es donde reside el reto: ¿cómo mantener la variedad y garantizar al mismo tiempo la precisión pedagógica?

Este es el problema que LearningLemur resuelve con su Modo Algoritmo. Ofrece a los educadores control sobre la lógica que hay detrás de la generación de valores aleatorios, transformando la variabilidad en una herramienta para la precisión.

Presentamos el Modo Algoritmo en LearningLemur

Esta potente función te permite, como educador, crear condiciones lógicas dinámicas y sofisticadas aprovechando la flexibilidad y la expresividad del código CalcMe. Más allá de las opciones lógicas estándar, ahora puedes manejar sin problemas valores aleatorios, criterios complejos y condiciones personalizadas directamente dentro de tu contenido educativo.

Con el Modo Algoritmo, podrás:

• Controlar con precisión la generación de valores aleatorios.
• Definir condiciones detalladas para excluir resultados específicos o garantizar las propiedades deseadas (por ejemplo, garantizar soluciones positivas, excluir resultados enteros o aplicar límites de rango).
• Definir condiciones precisas que controlen cómo interactúan los valores generados dentro de las expresiones matemáticas. Por ejemplo, garantizar que las variables estén siempre en un orden específico, que la ecuación sea resoluble o que los valores se relacionen proporcionalmente.

Todo esto es posible gracias a CalcMe, un potente lenguaje de programación ya integrado en los productos Wiris. Incluso si eres nuevo en la programación, CalcMe ofrece un enfoque sencillo para definir restricciones lógicas precisas sin la complejidad que suelen presentar los lenguajes de programación tradicionales.

El Modo Algoritmo es una función revolucionaria de LearningLemur. Permite a los educadores incorporar restricciones basadas en la lógica en sus flujos de trabajo de evaluación matemática, convirtiendo los valores aleatorios en prácticas con un propósito.

Con el Modo Algoritmo, puede aplicar lógica avanzada a sus problemas para, por ejemplo:

• Asegurarse de que las fracciones sean irreducibles haciendo que el numerador y el denominador tengan el máximo común divisor 1, de modo que mcd(numerador, denominador)==1.
• Controlar los dominios, asegurándose de que solo se utilicen números naturales o racionales.
• Garantizar la invertibilidad en las matrices.
• Exigir que los vectores sean paralelos.

Así es como el Modo Algoritmo pone en práctica estas ideas:

Ejemplo 1: Generar fracciones irreducibles.

Imagina que estás diseñando un ejercicio matemático en el que los alumnos deben sumar dos fracciones. Si estas se generan aleatoriamente, corres el riesgo de obtener fracciones como 4/2 o 6/3, valores que se simplifican a números enteros y frustran el objetivo de practicar con fracciones. Con el Modo Algoritmo, puedes asegurarte de que todas las fracciones generadas sean irreducibles, manteniendo el objetivo de aprendizaje enfocado y coherente.

# Generate the first fraction
# Choose a random numerator "a" from 1 to 9
a = random(1,9)    
# Define set "B" of denominators that are coprime with "a"
B = { b with b in 2..9 where gcd(a,b)=1 }  
# Choose random denominator "b" from set B
b = random(B)               

# Generate the second fraction
# Choose another random numerator "c" from 1 to 9
c = random(1,9)   
# Define set "D" of denominators coprime with "c", different from "b"
D = { d with d in 2..9 where gcd(c,d)=1 && d!=b } 
# Choose random denominator "d" from set "D"
d = random(D)                  

# Calculate the sum of the two irreducible fractions
# The solution the students will calculate
sol = a/b + c/d 

Ejemplo 2: Garantizar que las matrices sean invertibles

Supongamos que quieres que los alumnos practiquen el cálculo de la inversa de una matriz 2×2. Si la matriz se crea con valores aleatorios, es posible que algunas no sean invertibles, lo que haría que el problema fuera irresoluble. El Modo Algoritmo te permite filtrar estos casos, garantizando que cada matriz generada cumpla las condiciones necesarias para la inversión.

# Define a function to generate random integers
r() := random(-5,5) 

# Generate a matrix A (2x2) with a non-zero determinant, so invertible
repeat
    A = [ [r(), r()],
          [r(), r()]]
until determinant(A) != 0

# Define the matrix A^-1, inverse of A
sol= inverse(A)

Ejemplo 3: Controlar la orientación de los vectores

Piensa en una tarea en la que los alumnos deben calcular el producto escalar de vectores. Sin restricciones, los vectores generados aleatoriamente podrían apuntar en cualquier dirección, lo que alteraría la intención del ejercicio. Con el Modo Algoritmo, puede controlar cómo se relacionan los vectores entre sí, por ejemplo, asegurándose de que permanezcan paralelos u ortogonales en función de su objetivo de aprendizaje.

#Define u,v components without any zeros
u1=random([-20..20]/[0])
u2=random([-20..20]/[0])
v1=random([-20..20]/[0])
v2=random([-20..20]/[0])

#Create vectors u,v 

u=[u1,u2]
v=[v1,v2]

#Ensure they are orthogonal
while ((u*v)!=0) do
    v1=random([-20..20]/[0])
    v2=random([-20..20]/[0])
    v=[v1,v2]
end

Estos ejemplos muestran cómo el Modo Algoritmo eleva LearningLemur de un simple generador aleatorio a una herramienta inteligente de evaluación matemática impulsada por una lógica avanzada. Consulte nuestra documentación sobre el Modo Algoritmo para explorar todas las funciones de la herramienta, ver ejemplos prácticos y aprender a utilizarla de forma eficaz.

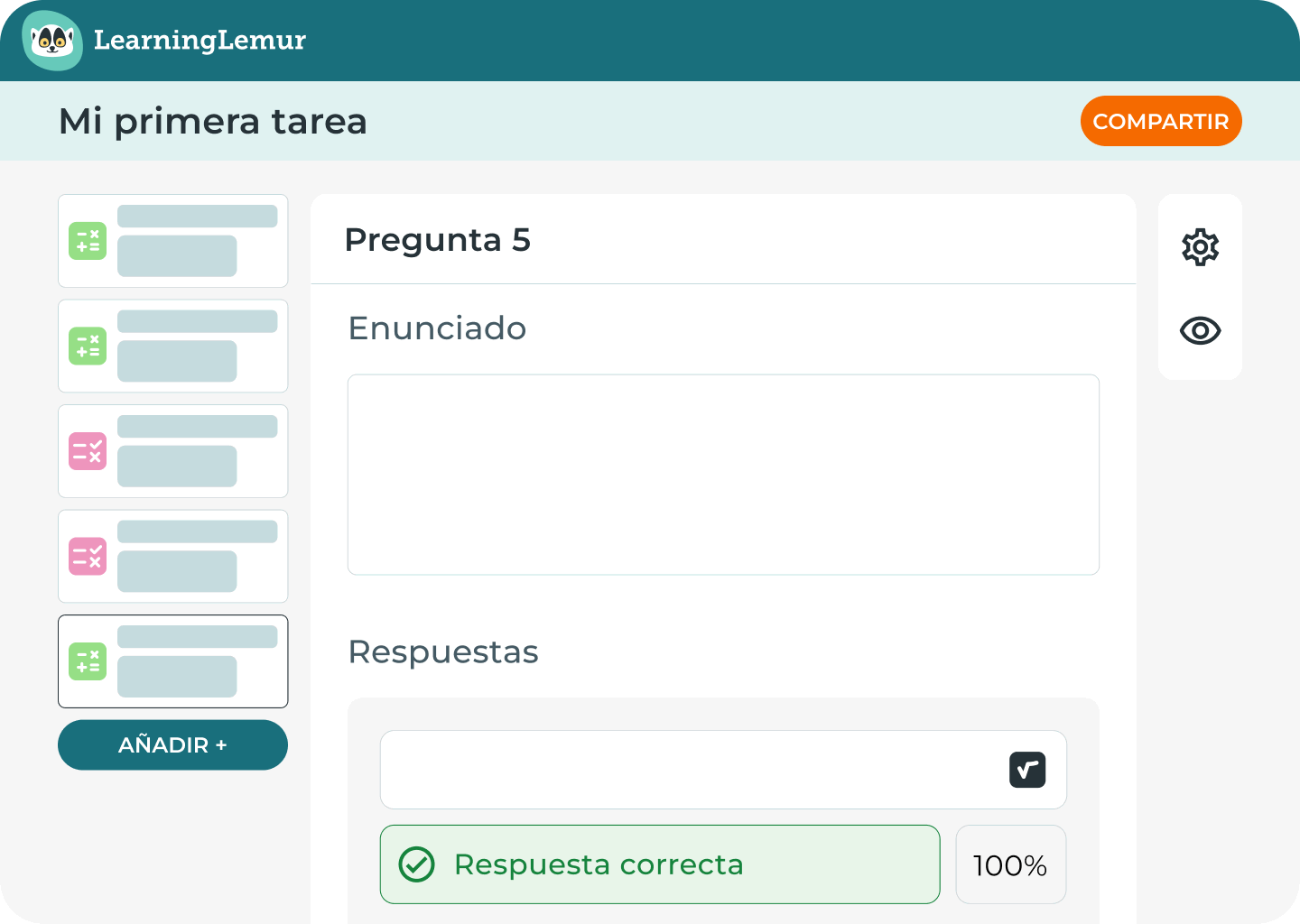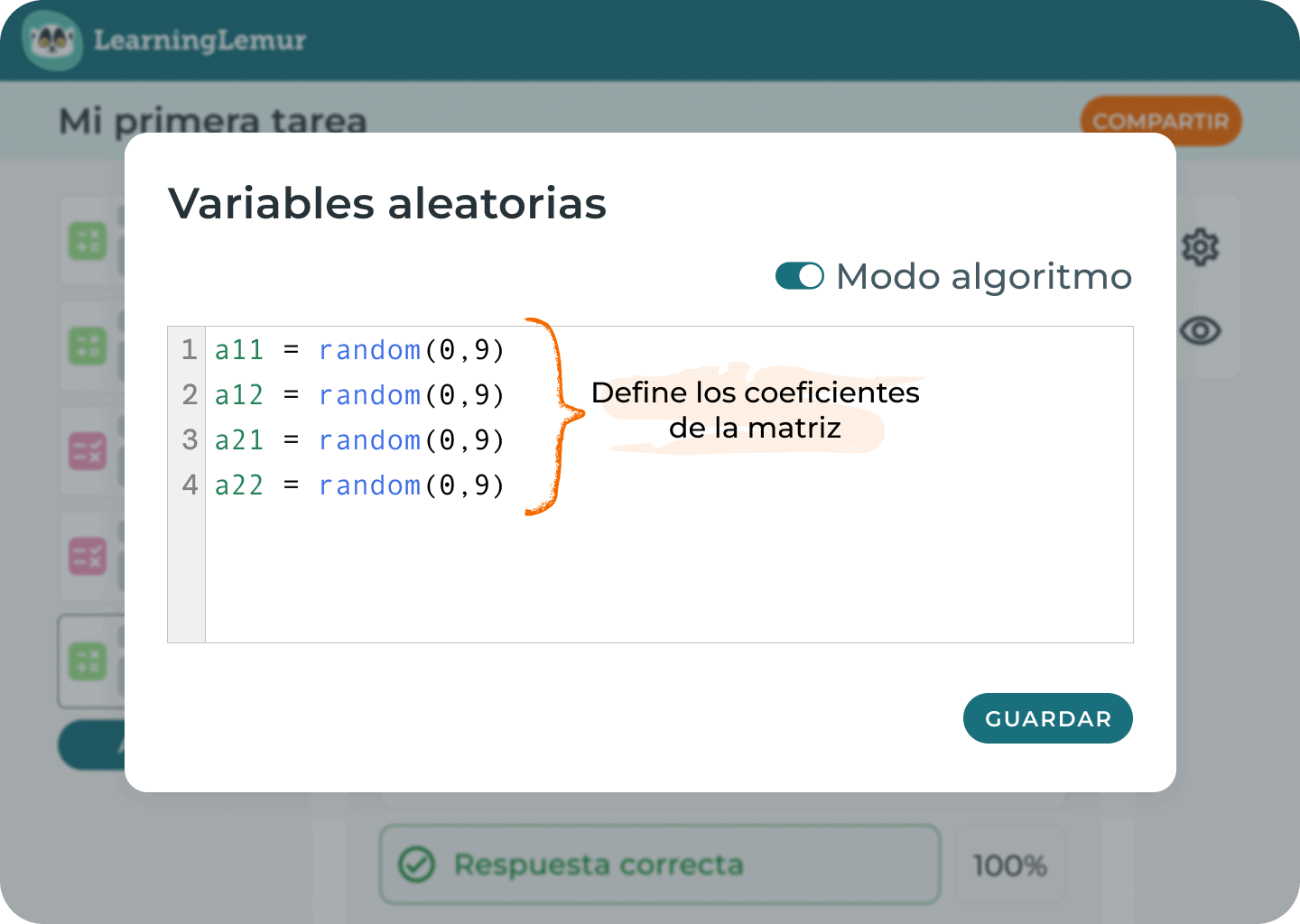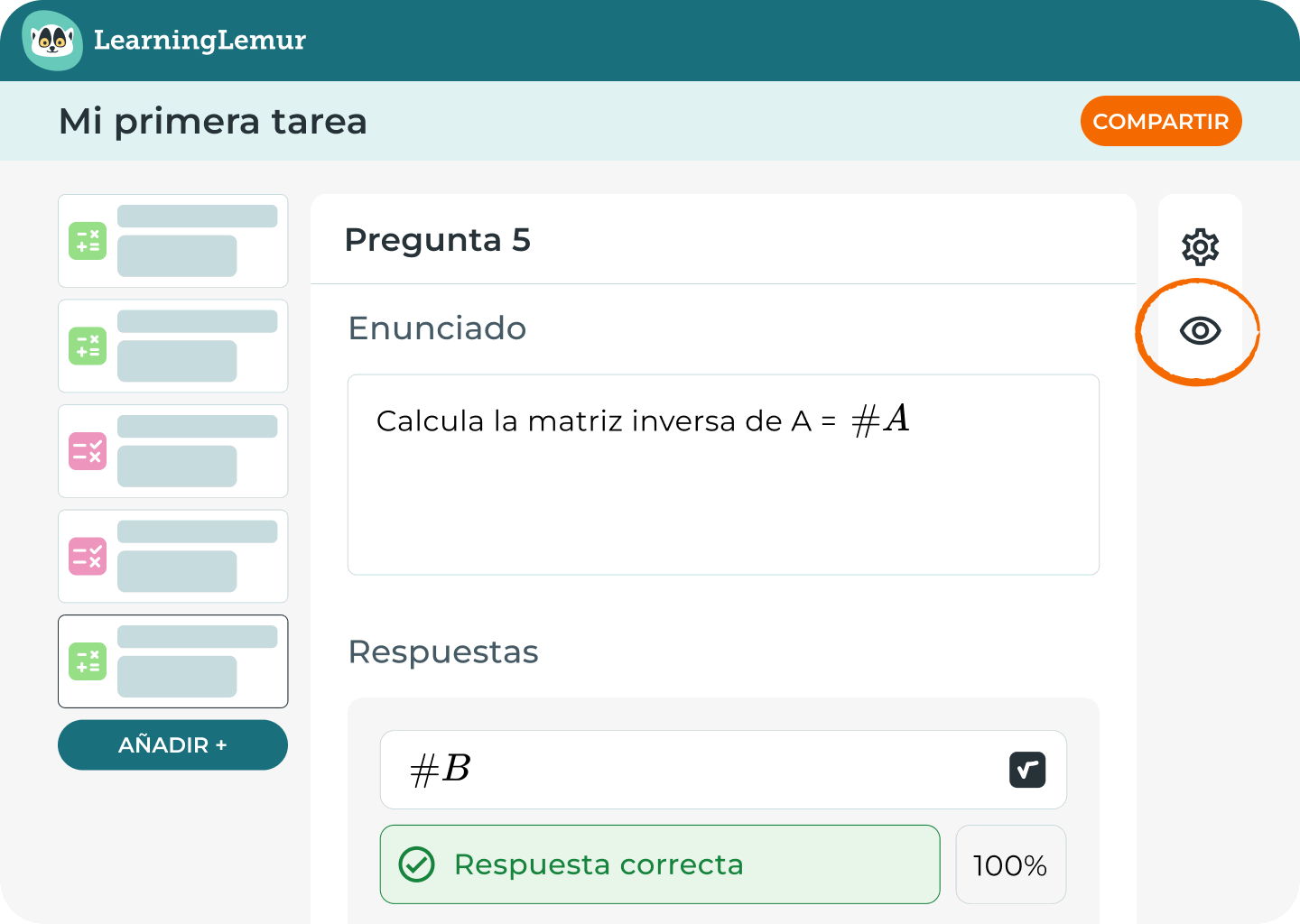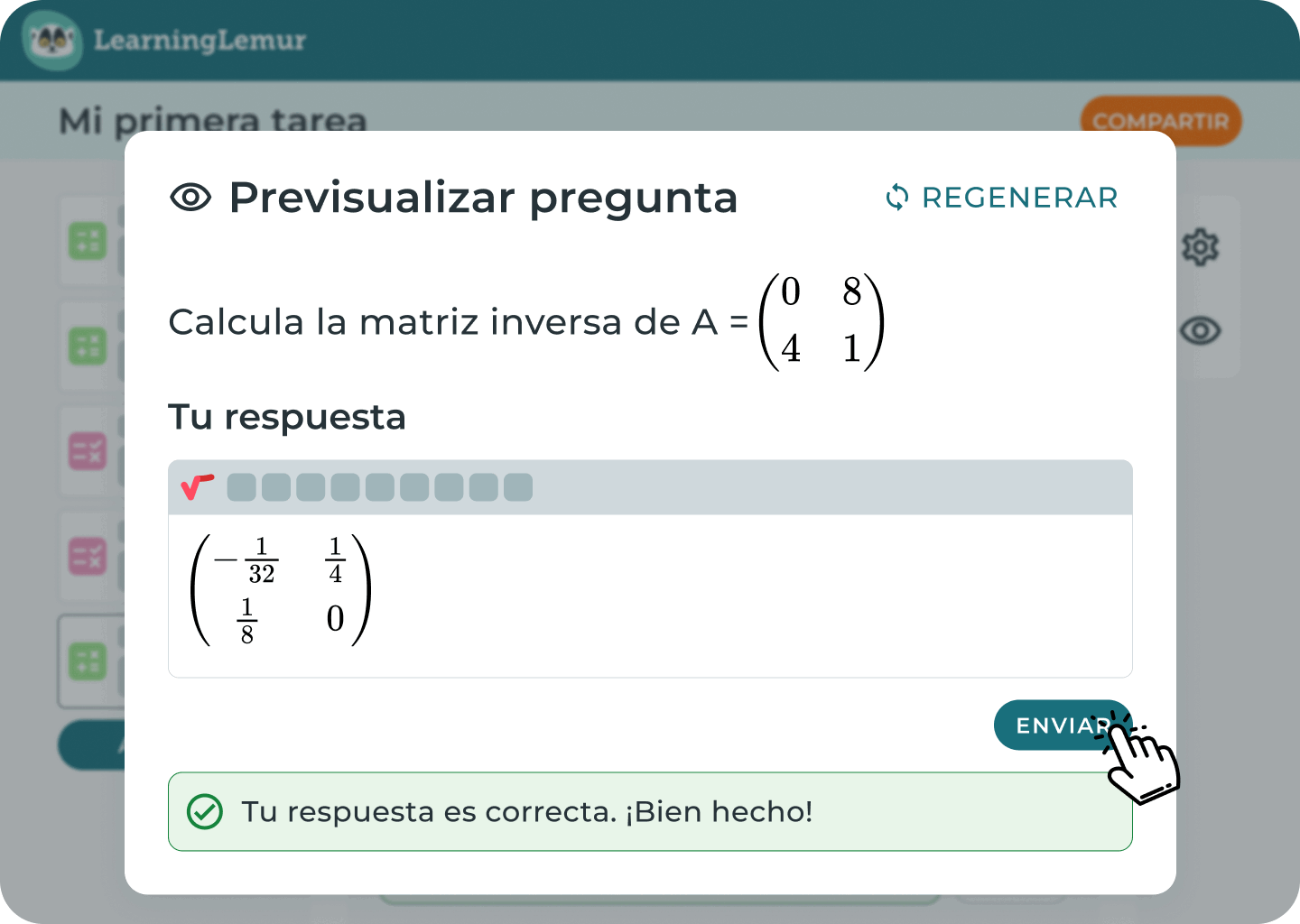
Por qué cada docente necesita el Modo Algoritmo

En cuanto empiezas a crear evaluaciones matemáticas que incluyen valores aleatorios, estás utilizando la lógica, ya sea de forma explícita o no. El Modo Algoritmo formaliza este proceso, haciéndolo repetible, escalable y alineado con tus objetivos de aprendizaje.

Los profesores se benefician de la coherencia, el control y la eficiencia. Ya no necesitan revisar cada versión de un problema. Los alumnos se benefician de itinerarios de aprendizaje más predecibles y retos que se ajustan a su nivel. Cuando los valores aleatorios se comportan de forma lógica, la educación se vuelve más precisa y atractiva.

Tanto si trabajas con aritmética elemental como con cálculo complejo, el Modo Algoritmo de LearningLemur te ayuda a centrarte en lo que más importa: el aprendizaje eficaz.

Las matemáticas más inteligentes comienzan con una lógica más inteligente

Esta mejora se suma a otro avance reciente de LearningLemur: un generador de evaluaciones matemáticas basado en inteligencia artificial que comprende tus necesidades y crea cuestionarios listos para usar en cuestión de segundos. Diseñada para ayudar a los profesores a poner en marcha evaluaciones matemáticas de forma eficiente, esta herramienta te permite:

• Describir el tipo de preguntas que deseas.
• Recibir al instante un conjunto de problemas matemáticos personalizados.
• Editarlos, perfeccionarlos y asignarlos directamente a tus alumnos.

Olvídate de empezar desde cero. Con esta función, trabajarás de forma más inteligente, no más dura, dentro de una plataforma intuitiva creada para educadores, incluso para aquellos con experiencia tecnológica limitada.

El Modo Algoritmo de LearningLemur supone un cambio revolucionario para la enseñanza digital de las matemáticas. Proporciona a los profesores las herramientas necesarias para guiar los valores aleatorios, en lugar de dejarse dominar por ellos. Tanto si está creando problemas con fracciones, diseñando ejercicios con vectores o construyendo matrices invertibles, el Modo Algoritmo garantiza que sus evaluaciones matemáticas siempre tengan sentido desde el punto de vista matemático.