La conjetura de Goldbach explicada: origen, demostración y matemáticas

Por qué este misterio matemático del siglo XVIII sigue fascinándonos

La conjetura de Goldbach es uno de los problemas no resueltos más antiguos y fascinantes de la teoría de números. Planteada por primera vez en el siglo XVIII, sigue siendo tan engañosamente simple como increíblemente difícil de demostrar. Tanto si eres docente de matemáticas como estudiante o simplemente un apasionado de la materia, comprender esta conjetura te abre una ventana a la elegancia de las matemáticas. En este artículo exploramos el origen de la conjetura de Goldbach, sus implicaciones y cómo herramientas como MathType pueden ayudarte a ilustrar ideas tan complejas en el aula.

La idea es aparentemente sencilla:

todo número entero par mayor que 2 puede expresarse como la suma de dos números primos.

Sorprendentemente, nadie ha conseguido todavía demostrar que esto sea cierto para todos los números pares. Y, sin embargo, a pesar de no existir una demostración general, millones de casos han confirmado su validez. ¿Cómo puede algo tan fácil de enunciar ser tan difícil de probar? Eso es precisamente lo que convierte la conjetura de Goldbach en un rompecabezas tan bello dentro de las matemáticas.

¿Qué afirma realmente la conjetura de Goldbach?

Aunque es fácil de entender, nadie ha sido capaz de demostrar esta afirmación para todos los números pares. Pero antes de analizar por qué esto es tan importante, veamos qué significa en la práctica.

Origen de la conjetura de Goldbach

La conjetura fue propuesta por primera vez por Christian Goldbach en una carta escrita en 1742 al célebre matemático Leonhard Euler. Goldbach afirmaba originalmente que todo número mayor que 2 podía escribirse como la suma de tres números primos (considerando al 1 como primo). Euler refinó lo que hoy llamamos la conjetura débil de Goldbach hasta llegar a la versión moderna que conocemos actualmente. Recuerda que un número primo es un número mayor que 1 que tiene exactamente dos divisores: 1 y él mismo.

Figura 1: Carta original de Goldbach a Euler con la proposición de la conjetura “débil” (1742).

Ejemplos numéricos

A continuación se muestran varios ejemplos de parejas de Goldbach para números pares:

• 4 = 2 + 2
• 6 = 3 + 3
• 8 = 3 + 5
• 10 = 3 + 7 o 5 + 5
• 12 = 5 + 7
• 14 = 3 + 11 o 7 + 7
• 16 = 3 + 13 o 5 + 11
• 18 = 5 + 13 o 7 + 11
• 20 = 3 + 17 o 7 + 13

Estos ejemplos ayudan al alumnado a visualizar cómo los números primos pueden combinarse de distintas formas para obtener el mismo número par. También dan pie a preguntas interesantes: ¿qué números pares tienen varias combinaciones de primos? ¿Existen algunos que solo tengan una?

Veamos más patrones:

• 28 = 5 + 23, 11 + 17
• 36 = 5 + 31, 7 + 29, 13 + 23, 17 + 19
• 50 = 3 + 47, 7 + 43, 13 + 37, 19 + 31, 23 + 27 (inválido), 29 + 21 (inválido)

Esto demuestra también que no toda suma de dos números impares da lugar a primos válidos. Es fundamental comprobar que ambos números de la pareja sean realmente primos.

¿Puede demostrarse? Intentos por resolver la conjetura

Aunque nadie ha demostrado de forma definitiva la conjetura de Goldbach, muchos matemáticos lo han intentado utilizando teoría de números avanzada, argumentos heurísticos o verificaciones mediante ordenador.

La conjetura se ha convertido en un reto de referencia: fácil de enunciar, pero con múltiples capas de complejidad matemática ocultas. Cada intento de demostrarla amplía los límites de nuestro conocimiento sobre la distribución de los números primos. La búsqueda de una demostración sigue siendo uno de los desafíos más apasionantes de las matemáticas modernas.

Verificación computacional

Gracias a la potencia de la computación moderna, la conjetura se ha verificado para todos los números pares hasta 4 × 10¹⁸, es decir, 4 quintillones. Esto significa que, para todos los números pares dentro de ese rango, se ha encontrado al menos una pareja de números primos cuya suma coincide con el número. Este enorme esfuerzo computacional ha requerido algoritmos inteligentes, técnicas de cribado de primos y redes de computación distribuida.

Pero aquí está el problema: por muy amplia que sea, la verificación computacional no equivale a una demostración. Solo confirma que la conjetura se cumple en todos los casos comprobados. Desde un punto de vista matemático, podría existir aún un contraejemplo más allá de ese límite.

Avances teóricos

Se han logrado varios resultados parciales importantes:

• Teorema de Vinogradov (1937): Demostró que todo número impar suficientemente grande puede escribirse como la suma de tres números primos. Aunque no es exactamente lo mismo, refuerza el espíritu de la idea de Goldbach.
• Deshouillers, Effinger, Granville y te Riele (1997): Bajo la Hipótesis Generalizada de Riemann, demostraron que la conjetura de Goldbach es válida para todos los números pares mayores que 4.
• Demostración de Helfgott (2013): Harald Helfgott demostró finalmente la conjetura débil de Goldbach (todo número impar mayor que 5 es la suma de tres primos).

Estos avances son hitos fundamentales, pero siguen dejando sin resolver la versión “fuerte”: todo número par mayor que 2 es la suma de dos primos. La comunidad matemática continúa buscando una demostración completa e incondicional.

¿Por qué nadie ha conseguido demostrarla todavía?

El problema está en la propia naturaleza de los números primos. Son los bloques fundamentales de todos los enteros, pero su distribución es irregular. A medida que los números crecen, los primos aparecen con menor frecuencia y de forma más impredecible.

Por ejemplo:

• Entre 10 y 20 hay cuatro primos: 11, 13, 17 y 19.
• Entre 90 y 100 solo hay dos: 89 y 97.

Esta distribución desigual complica enormemente la tarea de generalizar una regla válida para todos los números pares. Considera el número par 100:

• 100 = 3 + 97
• 100 = 11 + 89
• 100 = 17 + 83
• 100 = 29 + 71
• 100 = 41 + 59
• 100 = 47 + 53

Aunque existen muchas combinaciones, no se conoce ninguna fórmula que garantice este tipo de emparejamientos para todos los números pares.

Para demostrar la conjetura de Goldbach, sería necesario un método universal que probara que, para cualquier número par, siempre existe una pareja de números primos que lo sume. Pero actualmente no existe ningún método capaz de tener en cuenta la aparente aleatoriedad con la que aparecen los primos.

Además, el problema no se limita a una simple suma: está profundamente relacionado con la teoría analítica de números y con el comportamiento de la función zeta de Riemann, lo que lo convierte en un rompecabezas complejo y multidimensional.

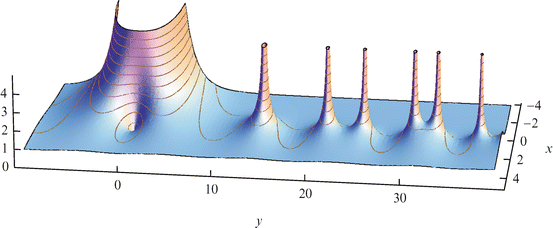
[IMAGEN: gráfico 3D de la función zeta de Riemann mostrando ceros complejos y su estructura]

Desde un punto de vista matemático, incluso expresar la densidad de primos que suman un número par concreto requiere herramientas avanzadas como el método del círculo o la teoría de cribas, que a su vez dependen de hipótesis que aún se están investigando.

Los números primos no son solo teoría: aplicaciones reales

Comprender los números primos no es solo un ejercicio teórico. Son fundamentales en ámbitos como:

• Criptografía: la seguridad de las comunicaciones depende de la dificultad de factorizar números primos grandes.
• Informática: muchos algoritmos utilizan primos para funciones hash y generación de números aleatorios.
• Compresión de datos y detección de errores: métodos basados en primos permiten una transmisión de datos fiable.

Esta relevancia práctica refuerza la importancia de conjeturas como la de Goldbach.

Explora, visualiza y enseña la conjetura de Goldbach con confianza

Algunas formas de explorar la conjetura de Goldbach de manera interactiva son:

• Elegir cualquier número par y encontrar todas sus parejas de Goldbach.
• Usar MathType para crear una tabla de números pares hasta 100 con todas las combinaciones válidas de primos.
• Analizar qué números primos aparecen con más frecuencia en las parejas.

Este enfoque práctico fomenta el pensamiento crítico y la creatividad matemática.

Da vida a las matemáticas con MathType

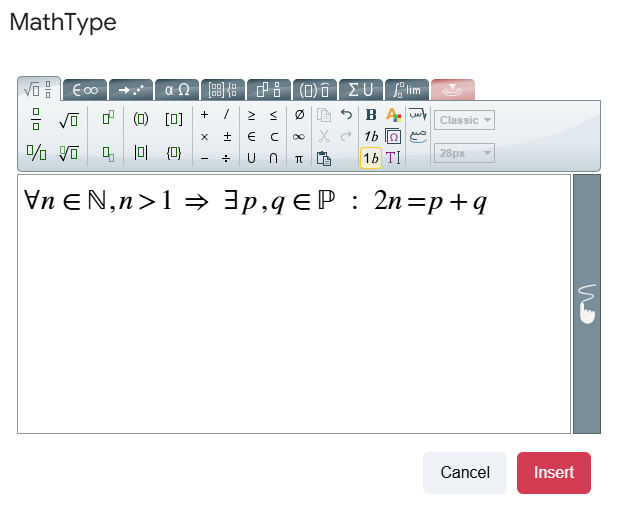
MathType de Wiris es un editor de ecuaciones que te permite escribir y presentar expresiones matemáticas de forma clara.

Con MathType, como docente puedes:

• Crear ejercicios para explorar parejas de Goldbach en distintos números pares.
• Presentar descomposiciones en números primos de forma visual.
• Diseñar actividades interactivas en las que el alumnado busque parejas de primos mediante patrones y deducción lógica.

MathType se integra con plataformas LMS, es compatible con LaTeX y simplifica la edición de ecuaciones tanto en web como en escritorio, lo que lo convierte en una herramienta ideal para el aula.

¿Quieres profundizar más en matemáticas?

La conjetura de Goldbach demuestra cómo de ideas simples pueden surgir preguntas profundas. Herramientas como MathType te permiten explorar estas ideas con claridad y precisión.

Prueba MathType y da vida a las expresiones matemáticas en tus clases o proyectos.