Solución paso a paso de un problema del examen de acceso a Oxford

Los exámenes de acceso a la Universidad de Oxford son famosos por su dificultad y por desafiar a los estudiantes con problemas matemáticos de gran complejidad. En este artículo, nos enfocaremos en un problema del examen de 2020 que consiste en calcular el área entre dos curvas. A través de un análisis claro y detallado, desglosaremos cada paso necesario para abordar y resolver este reto matemático.

Si te interesa, no dudes en visitar también nuestro otro artículo, «Cómo resolver una ecuación de grado 16«, donde exploramos otro problema desafiante del examen de Oxford.

El enunciado del problema es el siguiente:

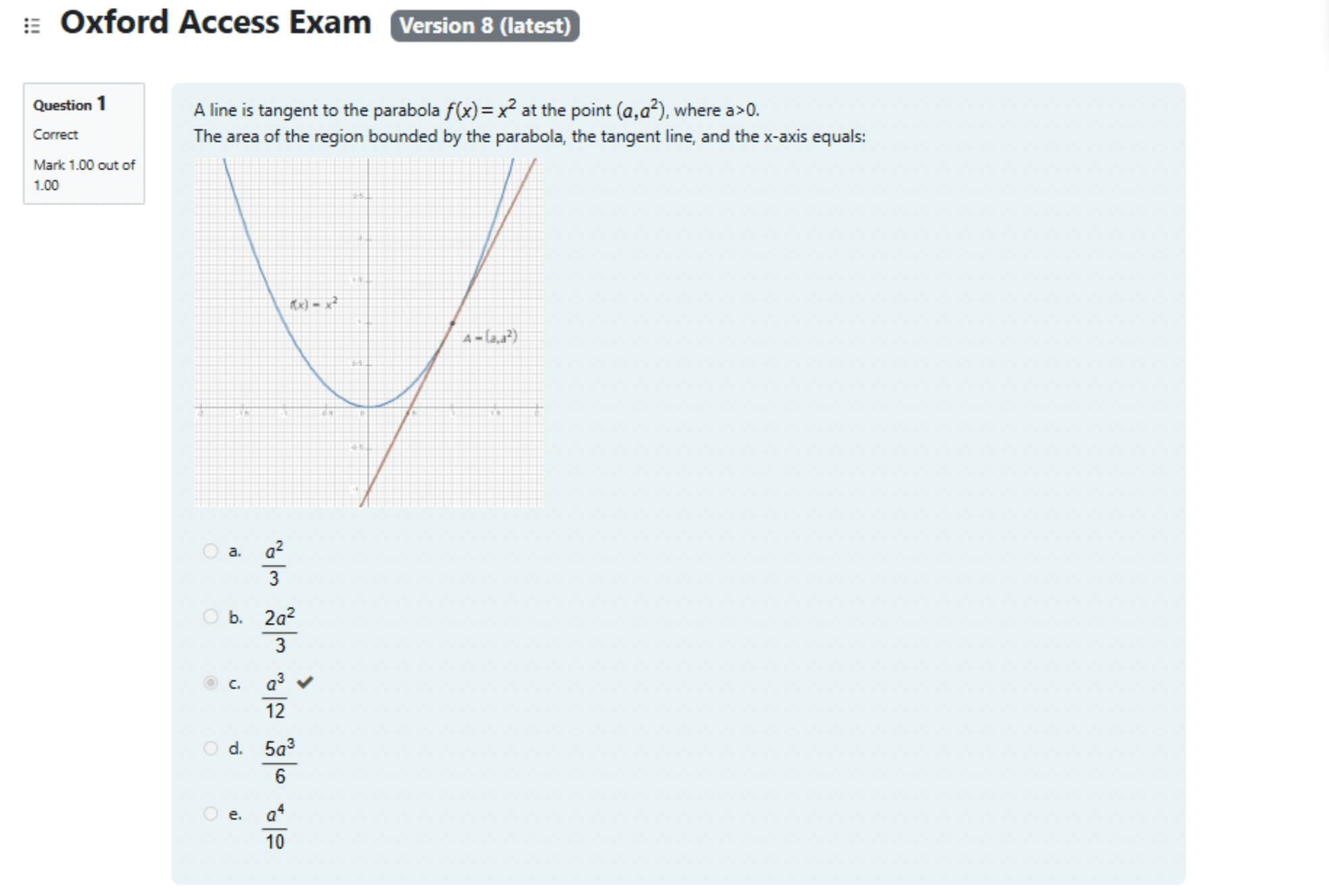
Una recta es tangente a la parábola y=x² en el punto (a,a²), donde a>0.

El área de la región delimitada por la parábola, la línea tangente y el eje x es igual a

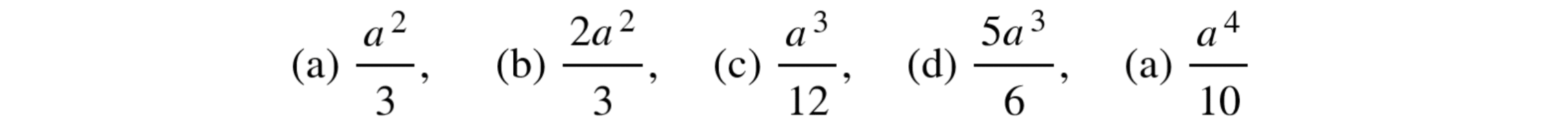
Este es un problema clásico de cálculo que, como veremos, requiere el uso tanto de derivadas como de integrales. No te preocupes, lo desglosaremos en tres pasos claros y sencillos. ¡Vamos a ello!

¿Cómo encontrar la ecuación de la recta tangente?

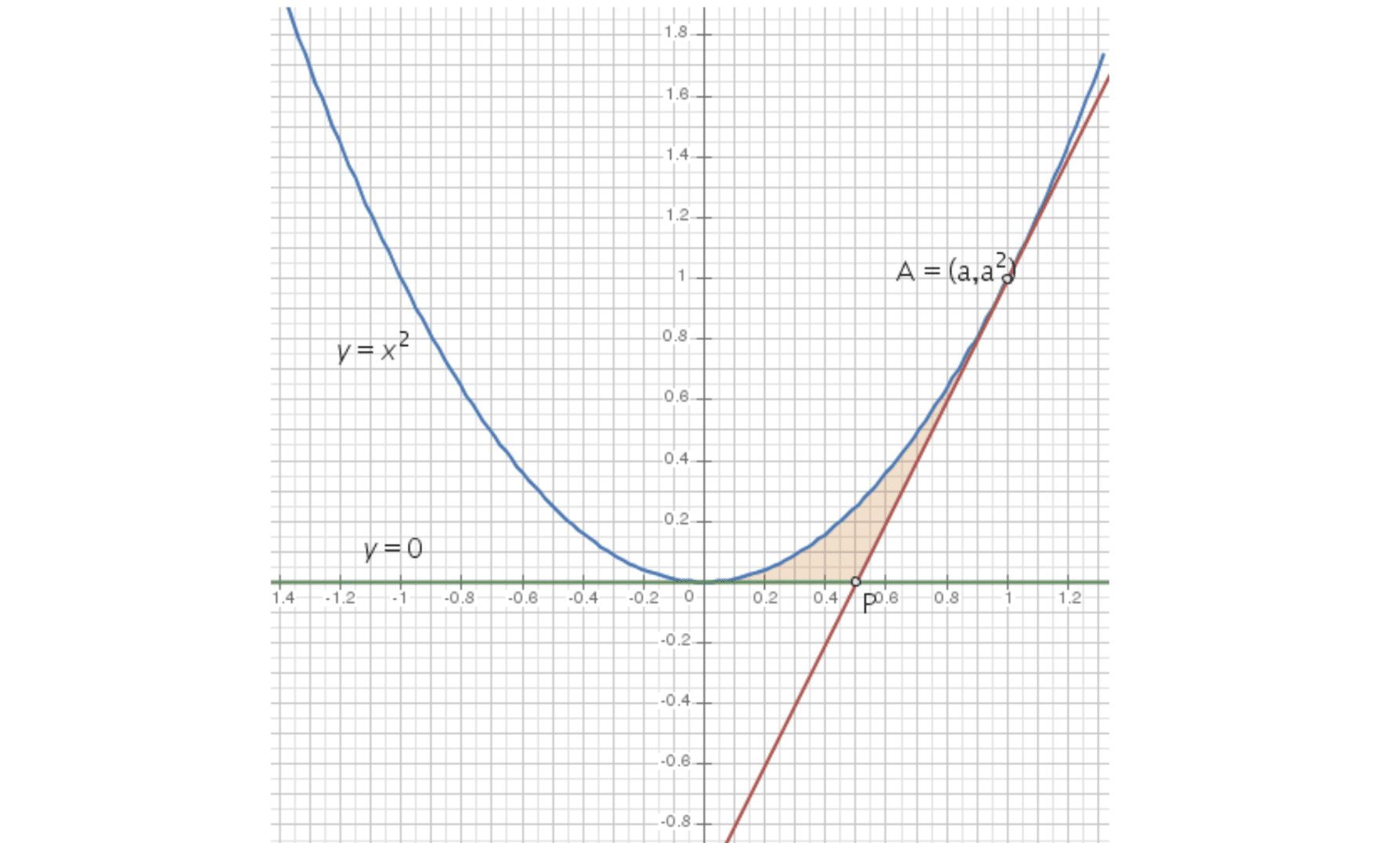
Antes de comenzar con los cálculos, visualicemos el problema. A continuación, hay un gráfico que ilustra la parábola y=x² y la línea tangente en el punto (a, a²), donde a>0. En este gráfico, se observa cómo la línea tangente toca la curva de la parábola en un único punto, sin cruzarla.

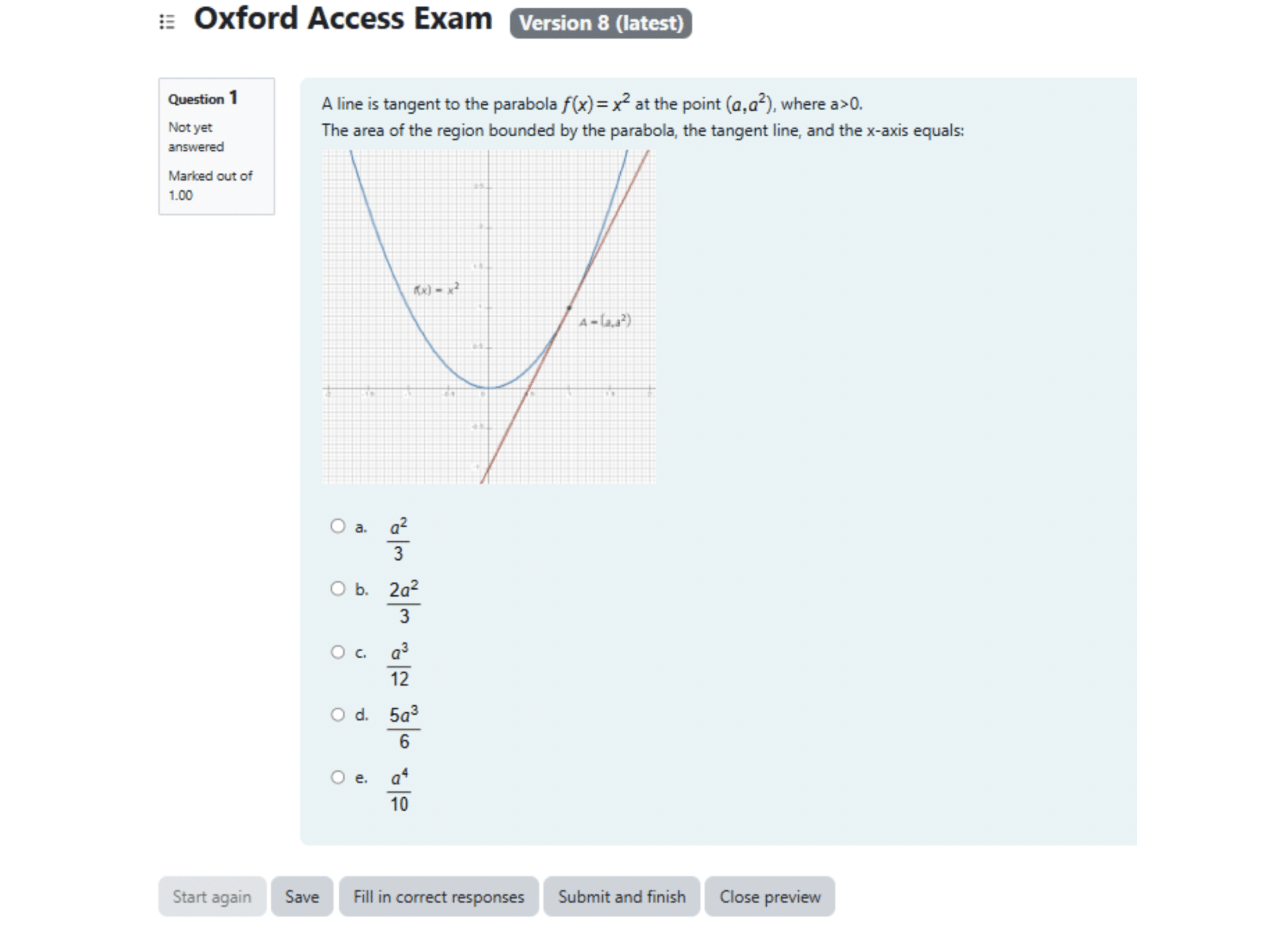
Ahora, para proceder, lo primero que debemos hacer es encontrar la ecuación de la recta tangente en ese punto específico. Dado que la tangente toca la parábola en el punto (a, a²), necesitamos determinar tanto su pendiente como su ecuación.

Aquí es donde entran en acción las derivadas. La pendiente de la tangente en cualquier punto de la parábola está dada por la derivada de la función y=x². Comenzamos calculando la derivada: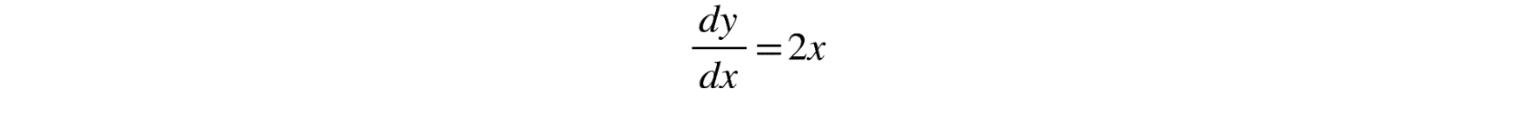

Esto significa que la pendiente de la tangente en cualquier punto de la parábola es 2x. Para encontrar la pendiente en el punto de tangencia (a, a²), sustituimos en la derivada:

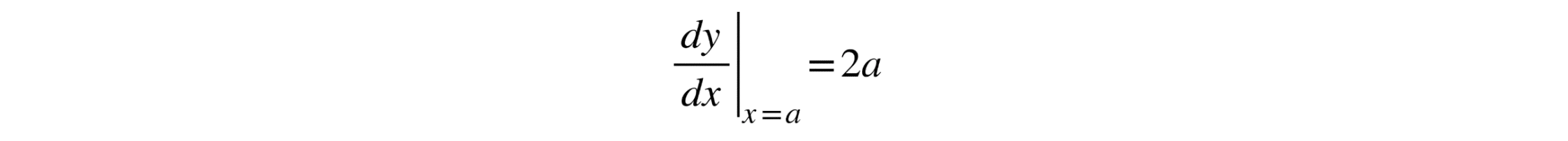
Por lo tanto, la pendiente de la recta tangente en el punto (a, a²) es 2a.

Ahora que tenemos la pendiente, podemos escribir la ecuación de la recta tangente utilizando la fórmula de la recta en su forma:

y – y₀ = m (x – x₀)

Donde es la pendiente de la recta, y (x₀ , y₀) es el punto por el cual pasa la recta. En nuestro caso, el punto de tangencia es y la pendiente es (a, a²), por lo que sustituimos estos valores en la fórmula de la recta:

y – a² = 2a (x-a)

y – a² = 2ax – 2a²

y = 2ax – a²

Así que, la ecuación de la recta tangente en el punto (a, a²) es:

y = 2ax – a²

Encontrar los puntos de intersección

Ahora que tenemos la ecuación de la tangente, necesitamos encontrar los puntos de intersección entre esta tangente y el eje x-axis, es decir, cuando y=0. Esto nos permitirá determinar los límites de la región cuya área queremos calcular.

El área a calcular está marcada en color naranja en el gráfico de abajo.

Sustituyendo y=0 en la ecuación de la tangente y despejando la x obtenemos:

0= 2ax – a²

2ax = a²

x = a/2

Así que la tangente corta el eje x-axis en el punto

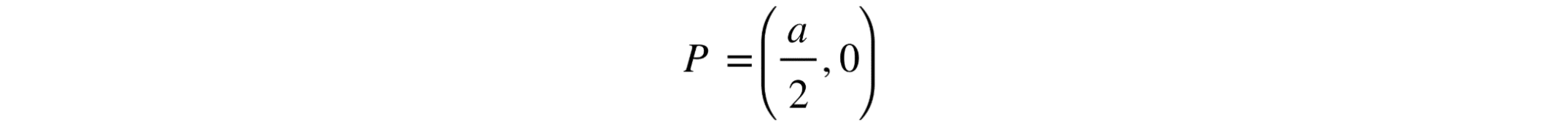
Calcular el área entre la parábola, la tangente y el eje x

Una vez que tenemos la ecuación de la tangente y sabemos los puntos de intersección, podemos proceder a calcular el área de la región limitada por la parábola, la tangente y el eje x-axis. Para esto, utilizamos la integral definida, que nos permite encontrar el área entre dos curvas.

El área que queremos calcular se obtiene restando dos regiones. En el primer gráfico, puedes observar la región total que nos interesa. Sin embargo, parte de esta área está delimitada de forma específica en el segundo gráfico, que debemos restar para quedarnos únicamente con la parte que buscamos.

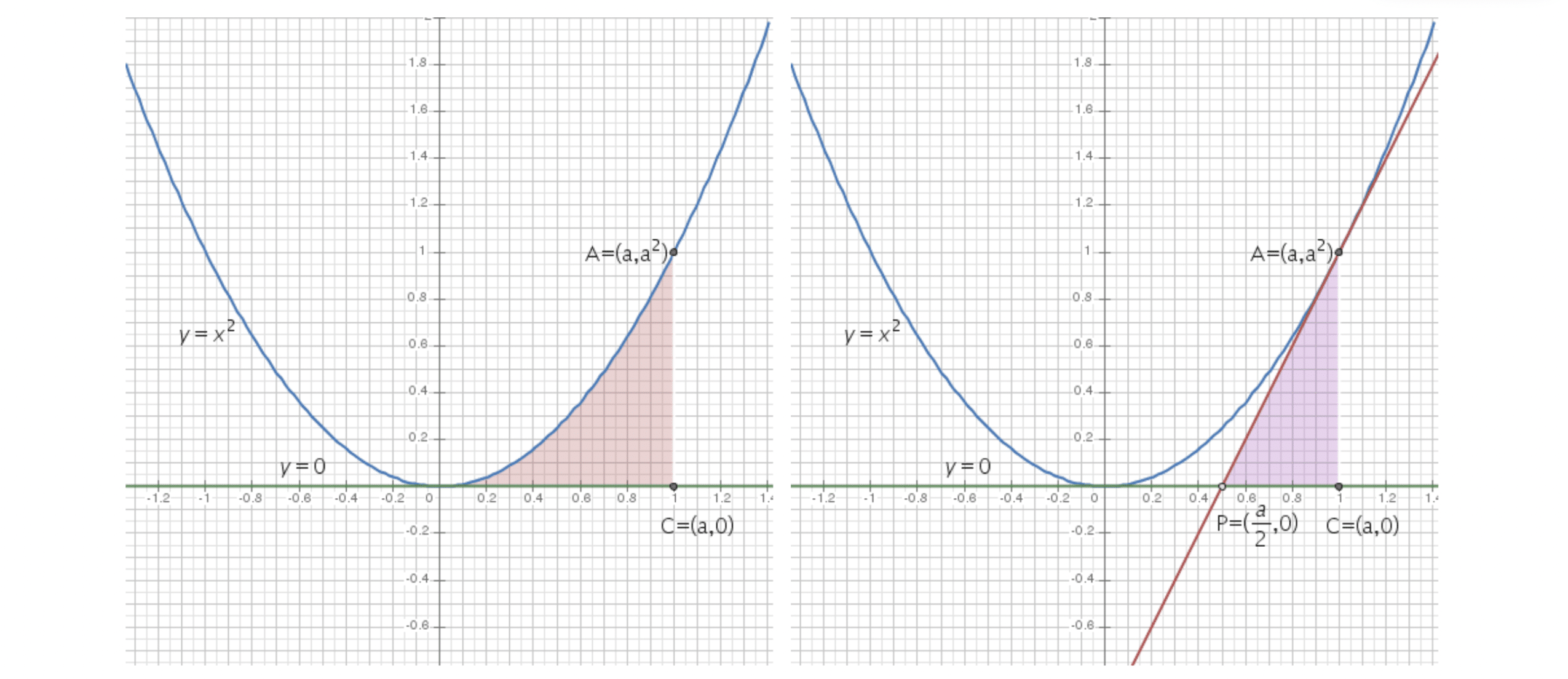
Calculemos ambas integrales:

1) Integral gráfico 1:

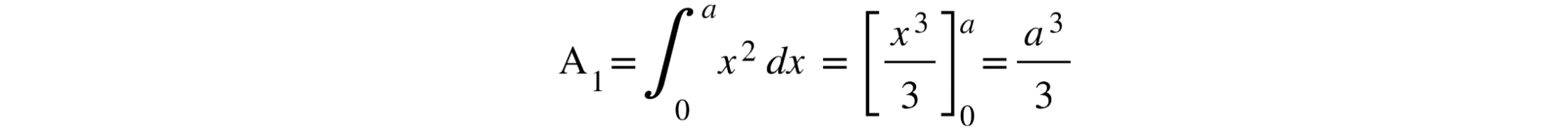
b) Integral gráfico 2:

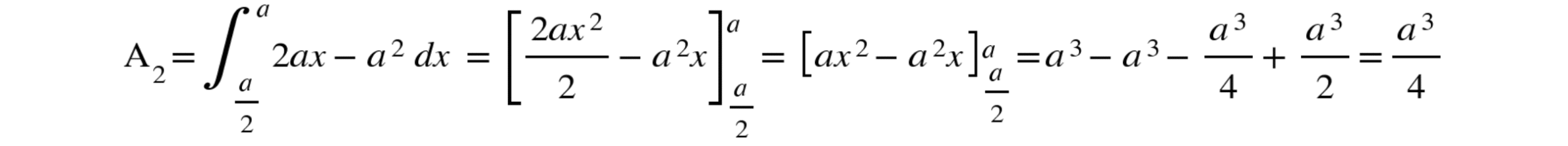
Ahora que hemos resuelto todas las integrales, restamos los resultados para obtener el área total:

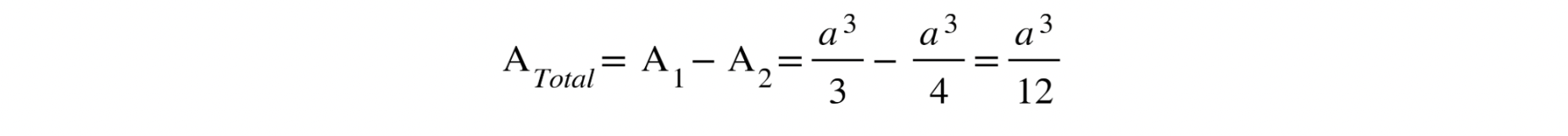
En conclusión, el área de la región delimitada por la parábola y = x², la tangente y = 2ax – a², y el eje x-axis, es:

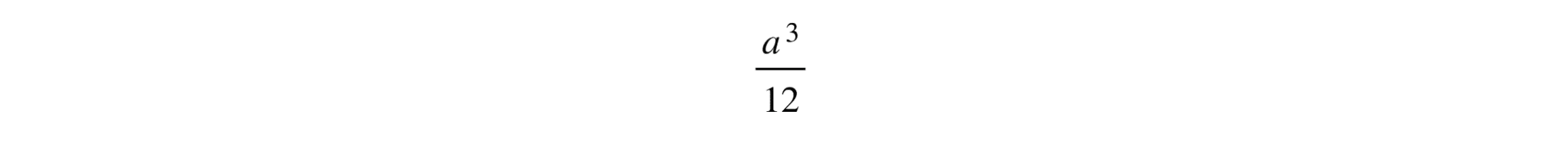
Por lo tanto, la respuesta correcta es la opción c.

¡Y así llegamos al final de este fascinante problema! Si has disfrutado este análisis o te ha resultado útil para entender mejor el proceso de resolución, ¡no dudes en compartirlo con otros apasionados de las matemáticas!

Ahora te lanzamos un reto: ¿te atreves a calcular el área formada por la curva y = x³ y su tangente en el punto (1,1)? Comparte tu solución o tus ideas en los comentarios. ¡Nos encantaría conocer tu enfoque!

Prueba WirisQuizzes para generar este ejercicio u otros

Compartir