Olimpiada Matemática: Resolviendo el primer problema de la IMO

Las competiciones matemáticas llevan mucho tiempo desafiando a los estudiantes a pensar de forma creativa y resolver problemas con elegancia y rigor. Entre ellas, la Olimpíada Matemática Internacional destaca como el escenario definitivo para los jóvenes talentos. Pero, ¿dónde comenzó todo? Revisemos el primer problema que se planteó en la IMO y descubramos cómo un algoritmo atemporal sigue siendo la clave para su solución.

1959: El nacimiento de una tradición matemática mundial

Era el año 1959. La Guerra Fría estaba en pleno apogeo y la educación, especialmente en ciencias y matemáticas, era considerada una prioridad estratégica por muchos países. En este contexto, Rumanía acogió la primera Olimpiada Internacional de Matemáticas, que reunió a estudiantes de siete países de Europa del Este. Esto marcó el comienzo de lo que se convertiría en la principal competición matemática del mundo.

En medio de las tensiones políticas de la época, este evento puso de manifiesto el poder de la colaboración y el desafío intelectual más allá de las fronteras. Los problemas seleccionados se diseñaron no solo para poner a prueba los conocimientos, sino también la creatividad y la elegancia en el razonamiento matemático.

Este es el problema original que se propuso en aquellas primeras Olimpiadas:

Demuestra que la fracción es irreducible para todo número natural n.

¿Qué es la Olimpíada Internacional de Matemática?

La Olimpiada Internacional de Matemáticas (OIM) es una de las competiciones matemáticas más prestigiosas del mundo. Desde su creación en 1959, ha sido una competición anual para estudiantes preuniversitarios a través de problemas complejos y elegantes. Organizada cada año por un país diferente, reúne a los jóvenes matemáticos más talentosos de todo el mundo. Los participantes se enfrentan a seis problemas durante dos días, cada uno de los cuales requiere una profunda comprensión y una resolución creativa.

A lo largo de los años, la OMI se ha convertido en un símbolo de excelencia en matemáticas. Muchos de los matemáticos de renombre de la actualidad comenzaron su andadura resolviendo problemas de la Olimpiada. Para los estudiantes, resolver problemas anteriores, como la primera pregunta de la OMI, no solo es enriquecedor desde el punto de vista intelectual, sino que también es una excelente preparación para futuras competiciones.

Cómo funciona el algoritmo euclidiano (y por qué es importante)

Para resolver el primer problema de la IMO, primero debemos comprender cómo calcular el máximo común divisor (MCD) de dos números. La forma más eficaz de hacerlo es mediante el algoritmo euclidiano, una técnica que se remonta a la antigua Grecia.H2: Introduce Another Key Aspect Logically

Paso a paso: el algoritmo euclidiano en acción

Así es como funciona:

1. Comienza con dos números enteros positivos, digamos A y B, donde A > B.
2. Divide A entre B y toma el resto R.
3. Reemplaza A por B y B por R.
4. Repite hasta que el resto sea 0.
5. El último resto distinto de cero es el MCD.

Ejemplo:

Vamos a hallar el MCD entre 252 y 105:

• 252 ÷ 105 = 2 el resto es 42 (puesto que: 252 – (105 X 2) = 42) 
• 105 ÷ 42 = 2 el resto es 21
• 42 ÷ 21 = 2 el resto es 0

Por lo tanto, el MCD de 252 y 105 es el último resto distinto de cero: 21.

Este algoritmo es extremadamente eficiente y funciona con cualquier par de números enteros. Lo verás en acción en breve.

Desglosando el método

Antes de profundizar en los pasos, aclaremos qué significa «mod». En matemáticas, «mod» significa módulo y se refiere al resto después de la división. Por ejemplo, 17 mod 5 = 2 porque 17 dividido por 5 es 3 con un resto de 2. Es un concepto clave en el algoritmo euclidiano para hallar el MCD.

Para demostrar que una fracción es irreducible, debemos mostrar que el numerador y el denominador no comparten divisores comunes distintos de 1. En otras palabras, su MCD debe ser 1.

Vamos a definir:

• A = 21n + 4
• B = 14n + 3

Debemos demostrar que MCD(A, B) = 1 para todos los números naturales n.

Usando el algoritmo euclidiano:

Paso 1: Calcular A mod B:

(21n + 4) mod (14n + 3)

Step 2: Resta una vez el denominador del numerador para hallar el resto. Calculamos:
(21n + 4) – 1x (14n + 3) = 21n + 4 – 14n – 3 = 7n + 1

Por lo tanto, el resto es 7n+1.

Step 3: A continuación:

(14n + 3) mod (7n + 1)

Calculamos:

(14n + 3) – 2x (7n + 1) = 14n + 3 – 14n – 2 = 1

Por lo tanto, el resto es 1.

Step 4: Dado que el resto es 1 y 1 es el MCD, la fracción original es irreducible.

Por lo tanto, para cada número natural n, es efectivamente irreducible.

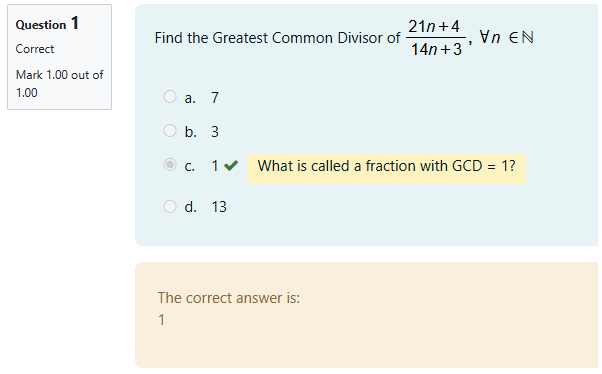
Pregunta generada con WirisQuizzes, una de las herramientas de evaluación de Wiris. 

Por qué es importante esta solución de la Olimpíada Matemática

La resolución de este problema demuestra cómo las técnicas matemáticas atemporales, como el algoritmo euclidiano, siguen siendo increíblemente poderosas. Incluso en concursos de alto nivel, muchas soluciones se basan en principios fundamentales que se enseñan en las primeras clases de álgebra.

La simplicidad de esta solución es parte de su belleza. Es una introducción perfecta para los estudiantes que se enfrentan a sus primeros problemas de la Olimpiada Matemática y un ejemplo inspirador de resolución elegante de problemas.

Aplicaciones del algoritmo euclidiano en el mundo real

Aunque este ejemplo proviene de una competición, el algoritmo euclidiano tiene usos en el mundo real:

• Criptografía: el algoritmo euclidiano es fundamental en el cifrado RSA, ya que ayuda a generar claves públicas y privadas. Se utiliza para calcular inversas modulares, esenciales para codificar y descodificar mensajes de forma segura a través de Internet. Sin él, muchos sistemas criptográficos no funcionarían de manera eficiente.
  
• Informática: en ingeniería de software, el algoritmo ayuda a simplificar las relaciones y a optimizar el código para problemas de teoría de números. Es especialmente útil en algoritmos relacionados con estructuras de datos, hash y sistemas distribuidos, donde la eficiencia es crucial.
  
• Ingeniería: los ingenieros aplican el algoritmo euclidiano en el procesamiento de señales para simplificar las relaciones de frecuencia y diseñar filtros. Ayuda a optimizar los sistemas de comunicación digital, garantizando la claridad y la precisión de las señales transmitidas a través de las redes.

Ya sea para resolver un problema de la Olimpiada Matemática o para optimizar algoritmos informáticos, comprender el MCD es inmensamente útil.

La importancia de facilitar la escritura matemática 

El mundo ha cambiado desde 1959. Hoy en día, con el auge del aprendizaje digital y la educación colaborativa, es esencial poder escribir notaciones matemáticas de forma clara y eficiente. Las herramientas educativas modernas ahora lo hacen más fácil que nunca, especialmente cuando se enseñan o resuelven problemas complejos como los de la Olimpiada Matemática. 

MathType de Wiris simplifica la escritura de ecuaciones matemáticas de forma digital, lo que permite a los estudiantes y educadores crear notaciones limpias y de aspecto profesional en plataformas como Google Docs, Microsoft Word y entornos LMS. Tanto si estás explicando el algoritmo euclidiano como si estás elaborando problemas de nivel olímpico, MathType te ayuda a centrarte en las matemáticas, no en el formato.

Además, las herramientas de evaluación de Wiris, entre las que se incluyen WirisQuizzes y LearningLemur, permiten a los educadores diseñar, impartir y calificar automáticamente evaluaciones matemáticas con precisión. Desde soluciones paso a paso hasta parámetros dinámicos, estas herramientas son ideales para evaluar los procesos de razonamiento, muy similares a los utilizados para demostrar la irreducibilidad en nuestro problema de la OMI. Aportan el rigor de la resolución de problemas al estilo de la Olimpiada al aula y ayudan a realizar un seguimiento del progreso real del aprendizaje.

Conclusión: brillantez en la Olimpiada Matemática desde el primer día

El primer problema de la Olimpiada Matemática, propuesto en 1959, fue una brillante combinación de simplicidad y profundidad. Aplicando el algoritmo euclidiano y comprendiendo la lógica detrás del MCD, demostramos que la fracción dada es irreducible para cualquier número natural.

Este tutorial no solo resuelve un problema histórico, sino que también muestra cómo las herramientas fundamentales pueden abordar retos sofisticados. Tanto si te estás preparando para tu próxima competición como si simplemente te encantan los rompecabezas matemáticos, siempre hay algo que aprender del pasado.